�P�Q�P�D�Q�O�O�V�N�̖��
 �O����X�܂ł̂P�O�̐������X�́��ɂP������ĉE�̌v�Z��������������ƁA�g��Ȃ��������P����܂��B
�O����X�܂ł̂P�O�̐������X�́��ɂP������ĉE�̌v�Z��������������ƁA�g��Ȃ��������P����܂��B
���̎g��Ȃ������Ƃ��čl��������̂����߁A���ׂē����Ă��������B
���̏o�T
�Z���I�����s�b�N�ɒ���
'00�`'03�N�x��
�Z���I�����s�b�N�ψ����
2003�N��V��W���j�A�Z���I�����s�b�N�t�@�C�i�����(����)
�����Ɖ��
�E����1
�i�y���l�|���F�l�c�@�����j
�����̂悤�ɁC�G�N�Z���̃}�N���ʼn������D
�`�a�b�{�c�d�e�{�f�g�h���Q�O�O�V�i�`�a�b<�c�d�e<�f�g�h�j�Ƃ��Čv�Z����D
���͂O�ƂX�̂Q�ł���D
Option Explicit
' ABC
' DEF
'+ GHI
'-----
' 2007 ({A,B,C,D,E,F,G,H,I}��{0,1,2,3,4,5,6,7,8,9},0<A<B<C)
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
Range("A1").Select
Dim A As Integer
Dim B As Integer
Dim C As Integer
Dim D As Integer
Dim E As Integer
Dim F As Integer
Dim G As Integer
Dim H As Integer
Dim I As Integer
Dim kuriagari(2) As Integer
Dim gyou As Integer
Dim retsu As Integer
Dim n As Integer
Dim nokori(9) As Integer
Dim j As Integer
For j = 0 To 9
nokori(j) = 0
Next j
For C = 0 To 9
For F = 0 To 9
If C <> F Then
'(C+F+I) mod 10=7
I = (10 + 7 - C - F) Mod 10
If C <> I And F <> I Then
kuriagari(1) = (C + F + I) \ 10
For B = 0 To 9
If B <> C And B <> F And B <> I Then
For E = 0 To 9
If B <> E And C <> E And E <> F And E <> I Then
'(B+E+H+kuriagari(1)) mod 10=0
H = (20 - B - E - kuriagari(1)) Mod 10
If B <> H And C <> H And E <> H And F <> H And H <> I Then
kuriagari(2) = (B + E + H + kuriagari(1)) \ 10
For A = 1 To 9 - 2
If A <> B And A <> C And A <> E And A <> F And A <> H And A <> I Then
For D = A + 1 To 9 - 1
If B <> D And C <> D And D <> E And D <> F And D <> H And D <> I Then
'A+D+G+kuriagari(2)=20
G = 20 - A - D - kuriagari(2)
If D < G And G <= 9 And B <> G And C <> G And E <> G And F <> G And G <> H And G <> I Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
gyou = Cells(1, 1).Value * 5 - 4
n = 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 - A - B - C - D - E - F - G - H - I
nokori(n) = nokori(n) + 1
Cells(gyou, 2).Value = A * 100 + B * 10 + C
Cells(gyou + 1, 2).Value = D * 100 + E * 10 + F
Cells(gyou + 2, 2).Value = G * 100 + H * 10 + I
Cells(gyou + 3, 2).Value = 2007
Cells(gyou + 3, 3).Value = n
Range("C" & (gyou + 3)).Select
End If
End If
Next D
End If
Next A
End If
End If
Next E
End If
Next B
End If
End If
Next F
Next C
retsu = 4 - 1
Range("D1").Select
For j = 0 To 9
If nokori(j) > 0 Then
retsu = retsu + 1
Cells(1, retsu).Value = j
End If
Next j
End Sub
�E����2
�i�y���l�|���FSOU�j
************************************************************ 1�̈ʂƂ��đI�ׂ���̂̑g�A�a�AID���ȉ��̂悤�ɐݒ肵�܂��B ************************************************************ ���̑g �a �gID 016 7 7a 025 7 7b 034 7 7c 124 7 7d 269 17 17a 278 17 17b 359 17 17c 368 17 17d 458 17 17e 467 17 17f ************************************************************************ ����ɘa��1�̈ʂ�0,9,8�ɂȂ鐔�̑g��ID���ȉ��̂悤�ɐݒ肵�܂��B ************************************************************************ 1�̈�0 ID 1�̈�9 ID 1�̈�8 ID 019 10a 018 9a 017 8a 028 10b 027 9b 026 8b 037 10c 036 9c 035 8c 046 10d 045 9d 126 8d 127 10e 126 9e 125 8e 136 10f 135 9f 134 8f 145 10g 234 9g 189 18a 235 10h 289 19a 279 18b 389 20a 379 19b 369 18c 479 20b 469 19c 378 18d 569 20c 478 19d 459 18e 578 20d 568 19e 468 18f 567 18g ************************************************************** ��Ƃɓ���܂��B ID:7a�`17f�̑S�Ă̍l�������̈ʂ̑g�ɑ��K���ȏ\�̈ʂ�I�сA ����ɂ���ɑ��ēK���ȕS�̈ʂ�I�т܂��B �g�ݍ��킹�����݂��Ȃ����ne�Ə����܂��B ************************************************************** ID �\�̈� �S�̈� �g�ݍ��킹 ���g�p�̐� 7a 10h 19d 016 235 478 9 20a ne 20b ne 20d ne 7b 10f 19d 025 136 478 9 20a ne 20b ne 7c 10e 19e 034 127 568 9 20c ne 20d ne 7d 10c 19e 124 037 568 9 20a 18g 124 389 567 0 20c 18d 124 569 378 0 20d 18c 124 578 369 0 17a 9a ne 9d ne 9f 19d 269 135 478 0 19d ne 17b 9c ne 9d ne 9f 19c 278 135 469 0 19c ne 17c 9a ne 9b ne 9e ne 19d ne 17d 9b ne 9d ne 17e 9b ne 9c ne 9e 19b 458 126 379 0 19b ne 17f 9a ne 9f 19a 467 135 289 0 19a ne ************************************************************************ �g�ݍ��킹�͂����ōl�������̈ȊO���݂��Ȃ��̂ŁA�g�킸�ɂ��ސ���0��9�őS�Ă� �Ȃ�܂��@// ************************************************************************
�ҎҒ��j�����ɍ����g�ݍ��킹�́A13�ʂ肠��܂��B
�E����3
�i�y���l�|���F�̂�����j
�R�̐���100a+10b+c,100d+10e+f,100g+10h+i �Ƃ��A���̂S�̏ꍇ�ɕ�����
�@�@�@(1)c+f+i=7,b+e+h=10 �̎�
�@�@�@(2)c+f+i=7,b+e+h=20 �̎�
�@�@�@(3)c+f+i=17,b+e+h=9 �̎�
�@�@�@(4)c+f+i=17,b+e+h=19 �̎�
(1)�̎��́@a+d+g=19�@�ƂȂ�悢
c+f+i+b+e+h=17�@������@a+d+g+x=45-17=28 x=28-19=9
���ۗ�E�E�E420,731,856
(2)�̎��́@a+d+g=18�@�ƂȂ�悢
c+f+i+b+e+h=27�@������@a+d+g+x=45-27=18 x=18-18=0
���ۗ�E�E�E531,682,794
(3)�̎��́@a+d+g=19�@�ƂȂ�悢
c+f+i+b+e+h=26�@������@a+d+g+x=45-26=19 x=19-19=0
���ۗ�E�E�E214,836,957
(4)�̎��́@a+d+g=18�@�ƂȂ�悢
c+f+i+b+e+h=36�@������@a+d+g+x=45-36=9 x=9-18=-9�@�ƂȂ�s�K
�@�@�@�@�@�i���j�O�ƂX
�E����4
�i�y���l�|���F�ɂ����j
��ӂ��A��̈ʂ̘a�́A�V�܂��͂P�V�̂��Âꂩ�ł���B
��̈ʂ̘a���V�̎��A
�\�̈ʂ̘a�́A�P�O�܂��͂Q�O�̂��Âꂩ�ł���B
��̈ʂ̘a���P�V�̎��A
�\�̈ʂ̘a�́A�X�܂��͂P�X�̂��Âꂩ�ł���B
�S�̈ʂ̘a�́A��̈ʁA�\�̈ʂ��킩��ΕK�R�I�ɋ��܂�̂ŁA�g�ݍ��킹�͈ȉ��̂S�ʂ�ƂȂ�B
�y�S�̈ʂ̘a�A�\�̈ʂ̘a�A��̈ʂ̘a�z��
�@�y�P�X�C�P�O�C�V�z�A�y�P�W�C�Q�O�C�V�z�A�y�P�X�C�X�C�P�V�z�A�y�P�W�C�P�X�C�P�V�z
�R�̐����̘a���V�ƂȂ�̂́A�ȉ��̂S�ʂ�B
�i�O�C�P�C�U�j�A�i�O�C�Q�C�T�j�A�i�O�C�R�C�S�j�A�i�P�C�Q�C�S�j
�R�̐����̘a���X�ƂȂ�̂́A�ȉ��̂V�ʂ�B
�i�O�C�P�C�W�j�A�i�O�C�Q�C�V�j�A�i�O�C�R�C�U�j�A�i�O�C�S�C�T�j
�i�P�C�Q�C�U�j�A�i�P�C�R�C�T�j�A�i�Q�C�R�C�S�j
�R�̐����̘a���P�O�ƂȂ�̂́A�ȉ��̂W�ʂ�B
�i�O�C�P�C�X�j�A�i�O�C�Q�C�W�j�A�i�O�C�R�C�V�j�A�i�O�C�S�C�U�j
�i�P�C�Q�C�V�j�A�i�P�C�R�C�U�j�A�i�P�C�S�C�T�j�A�i�Q�C�R�C�T�j
�R�̐����̘a���P�V�ƂȂ�̂́A�ȉ��̂W�ʂ�B
�i�O�C�W�C�X�j�A�i�P�C�V�C�X�j�A�i�Q�C�U�C�X�j�A�i�Q�C�V�C�W�j
�i�R�C�T�C�X�j�A�i�R�C�U�C�W�j�A�i�S�C�T�C�W�j�A�i�S�C�U�C�V�j
�R�̐����̘a���P�W�ƂȂ�̂́A�ȉ��̂V�ʂ�B
�i�P�C�W�C�X�j�A�i�Q�C�V�C�X�j�A�i�R�C�U�C�X�j�A�i�R�C�V�C�W�j
�i�S�C�T�C�X�j�A�i�S�C�U�C�W�j�A�i�T�C�U�C�V�j
�R�̐����̘a���P�X�ƂȂ�̂́A�ȉ��̂T�ʂ�B
�i�Q�C�W�C�X�j�A�i�R�C�V�C�X�j�A�i�S�C�U�C�X�j�A�i�S�C�V�C�W�j
�i�T�C�U�C�W�j
�R�̐����̘a���Q�O�ƂȂ�̂́A�ȉ��̂S�ʂ�B
�i�R�C�W�C�X�j�A�i�S�C�V�C�X�j�A�i�T�C�V�C�W�j�A�i�T�C�U�C�X�j
�P�j �y�S�̈ʂ̘a�A�\�̈ʂ̘a�A��̈ʂ̘a�z���y�P�X�C�P�O�C�V�z�̎�
�@��������g�ݍ��킹�́A
�y�i�S�C�V�C�W�j�C�i�P�C�R�C�U�j�C�i�O�C�Q�C�T�j�z �g��Ȃ��������X
�y�i�S�C�V�C�W�j�C�i�Q�C�R�C�T�j�C�i�O�C�P�C�U�j�z �g��Ȃ��������X
�y�i�T�C�U�C�W�j�C�i�O�C�R�C�V�j�C�i�P�C�Q�C�S�j�z �g��Ȃ��������X
�y�i�T�C�U�C�W�j�C�i�P�C�Q�C�V�j�C�i�O�C�R�C�S�j�z �g��Ȃ��������X
�Q�j �y�S�̈ʂ̘a�A�\�̈ʂ̘a�A��̈ʂ̘a�z���y�P�W�C�Q�O�C�V�z�̎�
��������g�ݍ��킹�́A
�y�i�R�C�U�C�X�j�C�i�T�C�V�C�W�j�C�i�P�C�Q�C�S�j�z �g��Ȃ��������O
�y�i�T�C�U�C�V�j�C�i�R�C�W�C�X�j�C�i�P�C�Q�C�S�j�z �g��Ȃ��������O
�y�i�R�C�V�C�W�j�C�i�T�C�U�C�X�j�C�i�P�C�Q�C�S�j�z �g��Ȃ��������O
�R�j �y�S�̈ʂ̘a�A�\�̈ʂ̘a�A��̈ʂ̘a�z���y�P�X�C�X�C�P�V�z�̎�
��������g�ݍ��킹�́A
�y�i�Q�C�W�C�X�j�C�i�P�C�R�C�T�j�C�i�S�C�U�C�V�j�z �g��Ȃ��������O
�y�i�R�C�V�C�X�j�C�i�P�C�Q�C�U�j�C�i�S�C�T�C�W�j�z �g��Ȃ��������O
�y�i�S�C�U�C�X�j�C�i�P�C�R�C�T�j�C�i�Q�C�V�C�W�j�z �g��Ȃ��������O
�y�i�S�C�V�C�W�j�C�i�P�C�Q�C�U�j�C�i�R�C�T�C�X�j�z �g��Ȃ��������O
�y�i�T�C�U�C�W�j�C�i�Q�C�R�C�S�j�C�i�P�C�V�C�X�j�z �g��Ȃ��������O
�y�i�S�C�V�C�W�j�C�i�P�C�R�C�T�j�C�i�Q�C�U�C�X�j�z �g��Ȃ��������O
�S�j �y�S�̈ʂ̘a�A�\�̈ʂ̘a�A��̈ʂ̘a�z���y�P�W�C�P�X�C�P�V�z�̎�
��������g�ݍ��킹�́A�Ȃ��B
�ȏ���A�g��Ȃ������́A�O�܂��͂X�ł���B
�E����5
�i�y���l�|���F�Z�g�l���Y�j
�h�P�h���s�[�X�ƌ��āA�O�`�X�̐��������ꂼ��̐��̃s�[�X��������
�e��ƍl���āA�J��オ����l���āE�E�E
�ꍇ��������
�P�O�̈ʂ��h�X�h�ň�̈ʂ��h�P�V�h�̂Ƃ�
�i�P�O�O�̈ʁj�W�|�U�|�T�i�P�O�̈ʁj�S�|�R�|�Q�i�P�̈ʁj�X�|�V�|�P
�i�P�O�O�̈ʁj�W�|�V�|�S�i�P�O�̈ʁj�T�|�R�|�P�i�P�̈ʁj�X�|�U�|�Q
�i�P�O�O�̈ʁj�W�|�V�|�S�i�P�O�̈ʁj�U�|�Q�|�P�i�P�̈ʁj�X�|�T�|�R
�i�P�O�O�̈ʁj�X�|�V�|�R�i�P�O�̈ʁj�U�|�Q�|�P�i�P�̈ʁj�W�|�T�|�S
�i�P�O�O�̈ʁj�X�|�W�|�Q�i�P�O�̈ʁj�T�|�R�|�P�i�P�̈ʁj�V�|�U�|�S
�i�P�O�O�̈ʁj�X�|�U�|�S�i�P�O�̈ʁj�T�|�R�|�P�i�P�̈ʁj�W�|�V�|�Q
�Łh�O�h���g���Ă��Ȃ�
�P�O�̈ʂ��h�P�O�h�ň�̈ʂ��h�V�h�̂Ƃ�
�i�P�O�O�̈ʁj�W�|�U�|�T�i�P�O�̈ʁj�P�|�Q�|�V�i�P�̈ʁj�S�|�R�|�O
�i�P�O�O�̈ʁj�W�|�V�|�S�i�P�O�̈ʁj�P�|�R�|�U�i�P�̈ʁj�T�|�Q�|�O
�i�P�O�O�̈ʁj�W�|�U�|�T�i�P�O�̈ʁj�R�|�V�|�O�i�P�̈ʁj�P�|�Q�|�S
�i�P�O�O�̈ʁj�W�|�V�|�S�i�P�O�̈ʁj�Q�|�R�|�T�i�P�̈ʁj�U�|�P�|�O
�Łh�X�h���g���Ă��Ȃ�
�P�O�̈ʂ��h�Q�O�h�ň�̈ʂ��h�V�h�̂Ƃ�
�i�P�O�O�̈ʁj�V�|�U�|�T�i�P�O�̈ʁj�X�|�W�|�R�i�P�̈ʁj�S�|�Q�|�P
�i�P�O�O�̈ʁj�W�|�V�|�R�i�P�O�̈ʁj�X�|�U�|�T�i�P�̈ʁj�S�|�Q�|�P
�i�P�O�O�̈ʁj�X�|�U�|�R�i�P�O�̈ʁj�W�|�V�|�T�i�P�̈ʁj�S�|�Q�|�P
�Łh�O�h�������Ă��Ȃ�
�����瓚���́A�h�O�h�Ɓh�X�h�łǂ��ł����H
�E����6
�i�y���l�|���F�܁[��j
�i�����j�O�C�X

�q�\�L�̃��[���r
�i�S�̈ʁj�i�S,�V,�W�j�Ə����A���̂R�̐�����S�̈ʂ̃}�X
�ia�Cb�Cc�j�̂����ꂩ�ɂǂ̏��Ԃœ���Ă��悢�Ƃ���B
�i�\�̈ʁj�i�Q,�R,�T�j�Ə����A���̂R�̐������\�̈ʂ̃}�X
�id�Ce�Cf�j�̂����ꂩ�ɂǂ̏��Ԃœ���Ă��悢�Ƃ���B
��̈ʂ����l�ł���B
�����āu�Q�O�O�V�v�ɂ���ɂ́A
�ȉ��́i�A�j�A�i�C�j�A�i�E�j�A�i�G�j�̏����̂����A�P�������K�v������B
�i�A�j�u�S�̈ʂ̘a�ia�{b�{c�j��19�v���u�\�̈ʂ̘a�id�{e�{f�j��10�v���u��̈ʂ̘a�ig�{h�{i�j���V�v
�i�C�j�u�S�̈ʂ̘a��18�v���u�\�̈ʂ̘a��20�v���u��̈ʂ̘a���V�v
�i�E�j�u�S�̈ʂ̘a��19�v���u�\�̈ʂ̘a���X�v���u��̈ʂ̘a��17�v
�i�G�j�u�S�̈ʂ̘a��18�v���u�\�̈ʂ̘a��19�v���u��̈ʂ̘a��17�v
�i�A�j�u�S�̈ʂ̘a�ia�{b�{c�j��19�v���u�\�̈ʂ̘a�id�{e�{f�j��10�v���u��̈ʂ̘a�ig�{h�{i�j���V�v�̂Ƃ�
�i�S�̈ʁ@�j�|�i�\�̈ʁj�|�i��̈ʁ@�j
�i�S,�V,�W�j�|�i�Q,�R,�T�j�|�i�O,�P,�U�j�E�E�E�g��Ȃ������́u�X�v
�i�S,�V,�W�j�|�i�P,�R,�U�j�|�i�O,�Q,�T�j�E�E�E�g��Ȃ������́u�X�v
�i�T,�U,�W�j�|�i�P,�Q,�V�j�|�i�O,�R,�S�j�E�E�E�g��Ȃ������́u�X�v
�i�T,�U,�W�j�|�i�O,�R,�V�j�|�i�P,�Q,�S�j�E�E�E�g��Ȃ������́u�X�v
�i�C�j�u�S�̈ʂ̘a��18�v���u�\�̈ʂ̘a��20�v���u��̈ʂ̘a���V�v�̂Ƃ�
�i�S�̈ʁ@�j�|�i�\�̈ʁj�|�i��̈ʁ@�j
�i�T,�U,�V�j�|�i�R,�W,�X�j�|�i�P,�Q,�S�j�E�E�E�g��Ȃ������́u�O�v
�i�R,�V,�W�j�|�i�T,�U,�X�j�|�i�P,�Q,�S�j�E�E�E�g��Ȃ������́u�O�v
�i�R,�U,�X�j�|�i�T,�V,�W�j�|�i�P,�Q,�S�j�E�E�E�g��Ȃ������́u�O�v
�i�E�j�u�S�̈ʂ̘a��19�v���u�\�̈ʂ̘a���X�v���u��̈ʂ̘a��17�v
�i�S�̈ʁ@�j�|�i�\�̈ʁj�|�i��̈ʁ@�j
�i�T,�U,�W�j�|�i�Q,�R,�S�j�|�i�P,�V,�X�j�E�E�E�g��Ȃ������́u�O�v
�i�S,�V,�W�j�|�i�P,�R,�T�j�|�i�Q,�U,�X�j�E�E�E�g��Ȃ������́u�O�v
�i�S,�U,�X�j�|�i�P,�R,�T�j�|�i�Q,�V,�W�j�E�E�E�g��Ȃ������́u�O�v
�i�S,�V,�W�j�|�i�P,�Q,�U�j�|�i�R,�T,�X�j�E�E�E�g��Ȃ������́u�O�v
�i�R,�V,�X�j�|�i�P,�Q,�U�j�|�i�S,�T,�W�j�E�E�E�g��Ȃ������́u�O�v
�i�Q,�W,�X�j�|�i�P,�R,�T�j�|�i�S,�U,�V�j�E�E�E�g��Ȃ������́u�O�v
�i�G�j�u�S�̈ʂ̘a��18�v���u�\�̈ʂ̘a��19�v���u��̈ʂ̘a��17�v�̂Ƃ�
���̏������������̑g�ݍ��킹�Ȃ��B
����āA�g���Ȃ������́A�O�ƂX�B
�E����7
�i�y���l�|���F�J�̖��j
3���̍��v��2007�ƂȂ�ɂ͌��ɒ��ڂ��čl����ƁA1����9�܂ł̑��a��45�ł���̂Ł@
3�̊e���̍��v��45�ȉ��ł��邱�Ƃ��K�v�Ȃ̂�
�@�@�@1900�@+�@100�@+�@7�@���@2007
�@�@�@1800�@+�@200�@+�@7�@���@2007
�@�@�@1900�@+�@90�@+�@17�@���@2007
�����Ȃ����Ƃ�������B������0�`9�܂ł�3���Â̘a�Ŋe�X�̌��̉\�����ȉ��̕\�ɐ�������ƁA
| 7 | 9 | 10 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|
| 016 | 018 | 019 | 089 | 189 | 289 | 389 |
| 025 | 027 | 028 | 179 | 279 | 379 | 479 |
| 034 | 036 | 037 | 269 | 369 | 469 | 569 |
| 124 | 045 | 046 | 278 | 459 | 478 | 578 |
| �@ | 126 | 127 | 359 | 378 | 568 | �@ |
| �@ | 135 | 136 | 368 | 468 | �@ | �@ |
| �@ | 234 | 145 | 458 | 567 | �@ | �@ |
| �@ | �@ | 235 | 467 | �@ | �@ | �@ |
�����āA��L�g�ݍ��킹�ɓK������悤3���̑��a���v�Z����B
�Ⴆ�A�ʼn����@�F�@016�@�A�������@�F�@235�@�A�@�ŏ㌅�@�F�@478�@��2007�ƂȂ�B
���̗l�Ɏ����Ă����ƁA0��9�͎g�p����Ȃ����Ƃ�������B
�����āA���߂���̂�0��9�ł���B
�E����8
�i�y���l�|���FMizuMini�j
A1 B1 C1
A2 B2 C2
+ A3 B3 C3
-----------
2 0 0 7
�����ŁA�e���ɂ��ĂP�O�O�̌����`�A�P�O�̌����a�A�P�̌����b�Ƃ��A�e���̐�����
���ꂼ��A��L�̂悤��A1�`C3�Ƃ��܂��B�P�D�ŏ��ɁA�b�̌��̐����̍��v�A�b�P�{�b�Q�{�b�R������l�́A�V���͂P�V�A�Q�V�A
�@ �R�V�����l�����܂����A�g����ő�̂R�̐����w�X�x�A�w�W�x�A�w�V�x�ł��̂ŁA�����
�@�����v���Ă��A�Q�S�ł��̂ŁA���v�͂V���͂P�V�ƂȂ�܂��B
�Q�D�܂��a�̌��ŁA�R�̐�����g�ݍ��킹�āA�a�̌����O�ɂ���ɂ́A
�@�@(1)�b�̌����V�Ō��オ��̂Ȃ��ꍇ�A�a�̌��̐����̍��v���P�O���͂Q�O�̓�ʂ�B
�@�@(2)�b�̌����P�V�Ō��オ�肪����ꍇ�A�a�̌��̐����̍��v���X���͂P�X�̓�ʂ�B
�R�D �������`�̌��ŁA�R�̐�����g�ݍ��킹�č��v���Q�O�ɂ���ɂ́A
�@�@(1)�a�̌����猅�オ�肪�Ȃ��ꍇ�A�`�̌��̐����̍��v���Q�O
�@�@(2)�a�̌�����P���オ�肪����ꍇ�A�`�̌��̐����̍��v�͂P�X
�@�@(3)�a�̌�����Q���オ�肪����ꍇ�A�@�`�̌��̐����̍��v�͂P�W
�S�D����āA�P�`�R�����e���̐����̍��v�Ł@���L��(1)�`(4)�̂S�ʂ�̑g�ݍ��킹��
�@�l�����܂��B
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| �� | �� | �� | �� | |
| �b�P�{�b�Q�{�b�R�� | �V | �V | �P�V | �P�V |
| �a�P�{�a�Q�{�a�R�� | �P�O | �Q�O | �X | �P�X |
| �`�P�{�`�Q�{�`�R�� | �P�X | �P�W | �P�X | �P�W |
�T�D���ܗ^����ꂽ�����́w�O�x����w�X�x�܂ł̐�����S�ĉ��Z����ƁA
�@�@�@�O+�P+�Q�{�R�{�S�{�T�{�U�{�V�{�W�{�X���S�T
�ƂȂ�̂ŁA���ꂩ��e���̐����̍��v�����������������߂鐔�l�ƂȂ�͂��ł��B
�@�@�@�S��(1)�̏ꍇ�A�@�S�T�|�i�P�X�{�P�O�{�V�j���X
�@�@�@�S��(2)�̏ꍇ�A�@�S�T�|�i�P�W�{�Q�O�{�V�j���O
�@�@�@�S��(3)�̏ꍇ�A�@�S�T�|�i�P�X�{�X�{�P�V�j���O
�@�@�@�S��(4)�̏ꍇ�A�@�S�T�|�i�P�V�{�P�X�{�P�W�j���|�X
�S��(4)�̏ꍇ�͕��ƂȂ�̂œK���܂���B�S��(2)�C(3)�̏ꍇ�́w�O�x�ł����A
�g���鐔���̒��Ɂw�O�x�������Ă܂��̂Ŗ�肠��܂���B����āA���߂�
�����́w�O�x���w�X�x�ƂȂ�܂��B
�U�D���������߂邽�߂Ɏ��ۂɐ����Ă͂߂Ă݂Ċm�F���Ă݂܂��B
�S��(1)�̏ꍇ�A �b�@�̌��̍��v���V�ɂ���ɂ́A
�w�O�C�Q�C�T�x�A�w�O�C�R�C�S�x�w�P�C�Q�C�S�x�A�w�P�C�U�C�O�x�̂S�ʂ�̑g�ݍ��킹���l�����܂��B
- �b�@�̌����w�O�C�Q�C�T�x�̏ꍇ�A�c��̐����ō��v���P�O�ɂȂ�g�ݍ��킹��
�w�P�C�R�C�U�x�݂̂ŁA�c��@�w�S�C�V�C�W�x�̍��v���P�X�ƂȂ�̂łn�j�ł��B
- �b�@�̌����w�O�C�R�C�S�x�̏ꍇ�A�c��̐����ō��v���P�O�ɂȂ�g�ݍ��킹��
�w�P�C�Q�C�V�x�݂̂ŁA�c��@�w�T�C�U�C�W�x�̍��v���P�X�ƂȂ�̂ł�����n�j�ł��B
- �b�@�̌����w�P�C�Q�C�S�x�̏ꍇ�A�c��̐����ō��v���P�O�ɂȂ�g�ݍ��킹��
�w�V�C�R�C�O�x�݂̂ŁA������c��@�w�T�C�U�C�W�x�ƂȂ�̍��v���P�X�ƂȂ�n�j�ł��B
- �b�@�̌����w�P�C�U�C�O�x�̏ꍇ�A�c��̐����ō��v���P�O�ɂȂ�g�ݍ��킹��
�w�T�C�R�C�Q�x�݂̂ŁA�c��@�w�S�C�V�C�W�x�̍��v���P�X�ƂȂ�̂ł�����n�j�ł��B
�S��(2)�̏ꍇ�A�b�̌��̍��v���V�ɂ���ɂ́A�w�P�C�Q�C�S�x�̑g�ݍ��킹�ŁA
�a�̌��̐��l�̍��v���P�W�ɂ���ɂ́w�R�C�W�C�X�x�A�w�T�C�U�C�X�x�A�w�T�C�V�C�W�x��
�R�ʂ�̑g�ݍ��킹���l�����܂��B
- �a�̌����w�R�C�W�C�X�x�̏ꍇ�A�c��w�T�C�U�C�V�x�̍��v���P�W�ƂȂ�̂łn�j�ł��B
- �a�̌����w�T�C�U�C�X�x�̏ꍇ�A�c��w�R�C�V�C�W�x�̍��v���P�W�ƂȂ�̂ł�����n�j�ł��B
- �a�̌����w�T�C�V�C�W�x�̏ꍇ�A�c��w�R�C�U�C�X�x�ƂȂ荇�v���P�W�ƂȂ�n�j�ł��B
�V�D�ȏ���A���߂鐔���́w�O�x�Ɓw�X�x�ł��B
�����F�w�O�x�Ɓw�X�x
�E����9
�i�y���l�|���FTo the stars�j
�܂��A100�̈ʂ�3�̐����̘a��19��18�̂����ꂩ�ł���B
�Ȃ��Ȃ�A10�̈ʂ�3�̐����̘a��10��20���̂����ꂩ�ł��邩��A
�K��100�̈ʂ�1��2�A�J��オ���Ă��邽�߁B
1) 100�̈ʂ̘a��19�ɂȂ�P�[�X
�@ ���s���ŁA
�@�@2-8-9�@�c�i�P�j
�@�@3-7-9�@�c�i�Q�j
�@�@4-6-9�@�c�i�R�j
�@�@4-7-8�@�c�i�S�j
�@�@5-6-8�@�c�i�T�j
�@ �̑g�ݍ��킹�̂݁B
2) 100�̈ʂ̘a��18�ɂȂ�P�[�X
�@ ���s���ŁA
�@�@1-8-9�@�c�i�U�j
�@�@2-7-9�@�c�i�V�j
�@�@3-6-9�@�c�i�W�j
�@�@3-7-8�@�c�i�X�j
�@�@4-6-8�@�c�i�P�O�j
�@�@5-6-7�@�c�i�P�P�j
�@ �̑g�ݍ��킹�̂݁B
���ɁA1�̈ʂ�3�̐����̘a��7��17�̂����ꂩ�ł���B
3) 1�̈ʂ̘a��7�ɂȂ�P�[�X
�@ ���s���ŁA
�@�@0-1-6
�@�@0-2-5
�@�@0-3-4
�@�@1-2-4
�@ �̑g�ݍ��킹�̂݁B
4) 1�̈ʂ̘a��17�ɂȂ�P�[�X
�@ ���s���ŁA
�@�@0-8-9
�@�@1-7-9
�@�@2-6-9
�@�@2-7-8
�@�@3-5-9
�@�@3-6-8
�@�@4-5-8
�@�@4-6-7
�@ �̑g�ݍ��킹�̂݁B
�i�P�j100�̈ʂ�(2-8-9)�̂Ƃ��A1�̈ʂ́A
�@�@0-1-6�@�i�c���3-4-5-7 10�͍�ꂸ�j
�@�@0-3-4�@�i�c���1-5-6-7�@10�͍�ꂸ�j
�@�@4-6-7�@�i�c���0-1-3-5�@9�����������g�p��0�j
�ł��邵���Ȃ��B
�i�Q�j100�̈ʂ�(3-7-9)�̂Ƃ��A1�̈ʂ́A
�@�@0-1-6�@�i�c���3-4-5-7�@10�͍�ꂸ�j
�@�@0-2-5�@�i�c���1-4-6-8�@10�͍�ꂸ�j
�@�@1-2-4�@�i�c���0-5-6-8�@10�͍�ꂸ�j
�@�@4-5-8�@�i�c���0-1-2-6�@9�����������g�p��0�j
�ł��邵���Ȃ��B
�i�R�j100�̈ʂ�(4-6-9)�̂Ƃ��A1�̈ʂ́A
�@�@0-2-5�@�i�c���1-3-7-8�@10�͍�ꂸ�j
�@�@2-7-8�@�i�c���0-1-3-5�@9�����������g�p��0�j
�ł��邵���Ȃ��B
�i�S�j100�̈ʂ�(4-7-8)�̂Ƃ��A1�̈ʂ́A
�@�@0-1-6�@�i�c���2-3-5-9�@10�����������g�p��9�j
�@�@0-2-5�@�i�c���1-3-6-9�@10�����������g�p��9�j
�@�@2-6-9�@�i�c���0-1-3-5�@9�����������g�p��0�j
�@�@3-5-9�@�i�c���0-1-2-6�@9�����������g�p��0�j
�ł��邵���Ȃ��B
�i�T�j100�̈ʂ�(5-6-8)�̂Ƃ��A1�̈ʂ́A
�@�@0-3-4�@�i�c���1-2-7-9�@10�����������g�p��9�j
�@�@1-2-4�@�i�c���0-3-7-9�@10�����������g�p��9�j
�@�@1-7-9�@�i�c���0-2-3-4�@9�����������g�p��0�j
�ł��邵���Ȃ��B
�i�U�j100�̈ʂ�(1-8-9)�̂Ƃ��A1�̈ʂ́A
�@�@0-2-5�@�i�c���3-4-6-7�@20�͍�ꂸ�j
�@�@0-3-4�@�i�c���2-5-6-7�@20�͍�ꂸ�j
�@�@4-6-7�@�i�c���0-2-3-5�@19�͍�ꂸ�j
�ł��邵���Ȃ��B
�i�V�j100�̈ʂ�(2-7-9)�̂Ƃ��A1�̈ʂ́A
�@�@0-1-6�@�i�c���3-4-5-8�@20�͍�ꂸ�j
�@�@0-3-4�@�i�c���1-2-5-6�@20�͍�ꂸ�j
�@�@3-6-8�@�i�c���0-1-4-5�@19�͍�ꂸ�j
�ł��邵���Ȃ��B
�i�W�j100�̈ʂ�(3-6-9)�̂Ƃ��A1�̈ʂ́A
�@�@0-2-5�@�i�c���1-4-7-8�@20�͍�ꂸ�j
�@�@1-2-4�@�i�c���0-5-7-8�@20�����������g�p��0�j
�@�@2-7-8�@�i�c���0-1-4-5�@19�͍�ꂸ�j
�ł��邵���Ȃ��B
�i�X�j100�̈ʂ�(3-7-8)�̂Ƃ��A1�̈ʂ́A
�@�@0-1-6�@�i�c���2-4-5-9�@20�͍�ꂸ�j
�@�@0-2-5�@�i�c���1-4-6-9�@20�͍�ꂸ�j
�@�@1-2-4�@�i�c���0-5-6-9�@20�����������g�p��0�j
�@�@2-6-9�@�i�c���0-1-4-5�@19�͍�ꂸ�j
�ł��邵���Ȃ��B
�i�P�O�j100�̈ʂ�(4-6-8)�̂Ƃ��A1�̈ʂ́A
�@�@0-2-5�@�i�c���1-3-7-9�@20�͍�ꂸ�j
�@�@3-5-9�@�i�c���0-1-2-7�@19�͍�ꂸ�j
�ł��邵���Ȃ��B
�i�P�P�j100�̈ʂ�(5-6-7)�̂Ƃ��A1�̈ʂ́A
�@�@0-3-4�@�i�c���1-2-8-9�@20�͍�ꂸ�j
�@�@1-2-4�@�i�c���0-3-8-9�@20�����������g�p��0�j
�@�@0-8-9�@�i�c���1-2-3-4�@19�͍�ꂸ�j
�ł��邵���Ȃ��B
�ȏ�ɂ��A0 �� 9 �ł���B�E�E�E�i���j
�E����10
�i�y���l�|���F�܂��܂��^�R����j
�F�@�O�@�Ɓ@�X
�ߒ��F
��̈�
��肩��A�O�`�X�̐����R�𑫂��āi���������͎g��Ȃ��j�v�Z���ʂ̈�̈ʂ��u�V�v�ɂ��Ȃ���Ȃ�܂���B
�O�`�X�̂����A�R�̐����𑫂��ďo����v�Z���ʂ͍ŏ��Łu�R�v�i���O�{�P�{�Q�j�ŁA�ő�́u�Q�S�v�i���V�{�W�{�X�j�ł��B
�R�`�Q�S�̂����A��̈ʂ��u�V�v�Ȃ̂́A�V�@�Ɓ@�P�V�@�ł��B
�\�̈�
�����悤�ɁA�R�̐����̍��v�̈�̈ʂ��u�O�v�ɂȂ�Ȃ���Ȃ�܂���B
�R�`�Q�S�̂����A��̈ʂ��u�O�v�Ȃ̂́A�P�O�@�Ɓ@�Q�O�@�ł��B
����ɁA�u��̈ʁv���u�P�V�v�̂Ƃ��̌J��オ�肪����̂ŁA�X�@�Ɓ@�P�X�@���l���Ȃ�������܂���B
�S�̈�
�����́A���v���u�Q�O�v�ɂȂ�Ȃ�������܂���B
�\�̈ʂ̌J��オ�肪�A�u�P�v�̂Ƃ��ƁA�u�Q�v�̂Ƃ�������̂ŁA�R�̐����̍��v���A�P�W�@�Ɓ@�P�X�@�ł��B
�܂Ƃ߂�ƁA�R�̐����̍��v�����ꂼ��A
�@��̈ʁE�E�E�E�E�V�A�P�V
�@�\�̈ʁE�E�E�E�E�X�A�P�O�A�P�X�A�Q�O
�@�S�̈ʁE�E�E�E�E�P�W�A�P�X
�̂Ƃ��ɁA�v�Z���ʂ��u�Q�O�O�V�v�ɂȂ蓾�܂��B
�����ŁA�u�Q�O�O�V�v�ɂȂ�g�ݍ��킹���l����ƁA
�@�S�̈ʁ@�\�̈ʁ@��̈�
�@�P�W�@�|�@�P�X�@�|�@�P�V�@�E�E�E�E�E(1)
�@�P�W�@�|�@�Q�O�@�|�@�V�@�E�E�E�E�E�E(2)
�@�P�X�@�|�@�X�@�@�|�@�P�V�@�E�E�E�E�E(3)
�@�P�X�@�|�@�P�O�@�|�@�V�@�E�E�E�E�E�E(4)
�̂S�ʂ�ɂȂ�܂��B
�����ŁA�O�`�X�̂����A�X�̐����𑫂��āi���������͎g��Ȃ��j�o����v�Z���ʂŁA
�ŏ��́u�R�U�v�i�O�{�P�{�Q�{�E�E�E�{�W�j�ŁA
�ő�́u�S�T�v�i�P�{�Q�{�R�{�E�E�E�{�X�j�ł��B
��̑g�ݍ��킹�̂����A�R�̐����̍��v���A�R�U�`�S�T�̊ԂɂȂ���A�u�O�`�X���P��Âg���āv�͕s�\�ƂȂ�܂��B
(1)�́@�T�S�@�ɂȂ��āA�������͂���܂��B
(2)(3)�́@�S�T�@�ŁA�����ɂ����܂��B�g�p���Ȃ������͏�̊��ʓ��̎����u�@�O�@�v�ł��B
(4)�́@�R�U�@�ŁA����������ɂ����܂��B�g�p���Ȃ������́u�@�X�@�v�ł��B
��L���A�����́@�O�@�Ɓ@�X�@�ɂȂ�܂��B
���Ƃ́A��̑g�ݍ��킹�̒��ŁA�����������Q��ȏ�g�킸�ɁA
�R�̐����̍��v�̑g�ݍ��킹����L�̂悤�ɏo���邩���ؖ����Ȃ���Ȃ�Ȃ��Ǝv���܂��B
�܂��A�u�V�v�́A�O�`�X�̓��łR�̈قȂ鐔���̘a�ŕ\����
�u�O�{�P�{�U�v�A�u�O�{�Q�{�T�v�A�u�O�{�R�{�S�v�A�u�P�{�Q�{�S�v���l�����܂��B���̐��������l�ɁE�E�E
| �V | �i�O�C�P�C�U�j�i�O�C�Q�C�T�j�i�O�C�R�C�S�j�i�P�C�Q�C�S�j |
|---|---|
| �X | �i�O�C�P�C�W�j�i�O�C�Q�C�V�j�i�O�C�R�C�U�j�i�O�C�S�C�T�j�i�P�C�Q�C�U�j�i�P�C�R�C�T�j�i�Q�C�R�C�S�j |
| �P�O | �i�O�C�P�C�X�j�i�O�C�Q�C�W�j�i�O�C�R�C�V�j�i�O�C�S�C�U�j�i�P�C�Q�C�V�j�i�P�C�R�C�U�j�i�P�C�S�C�T�j�i�Q�C�R�C�T�j |
| �P�V | �i�O�C�W�C�X�j�i�P�C�V�C�X�j�i�Q�C�U�C�X�j�i�Q�C�V�C�W�j�i�R�C�T�C�X�j�i�R�C�U�C�W�j�i�S�C�T�C�W�j �i�S�C�U�C�V�j |
| �P�W | �i�P�C�W�C�X�j�i�Q�C�V�C�X�j�i�R�C�U�C�X�j�i�R�C�V�C�W�j�i�S�C�T�C�X�j�i�S�C�U�C�W�j�i�T�C�U�C�V�j |
| �P�X | �i�Q�C�W�C�X�j�i�R�C�V�C�X�j�i�S�C�U�C�X�j�i�S�C�V�C�W�j�i�T�C�U�C�W�j |
| �Q�O | �i�R�C�W�C�X�j�i�S�C�V�C�X�j�i�T�C�U�C�X�j�i�T�C�V�C�W�j |
���̒��ŁA��̑g�ݍ��킹���Q�l�Ɂi�@�j���ɂO�`�X���Q��ȏ�o�Ă��Ȃ��g�ݍ��킹���l���܂����B
�S�̈ʁ@�@�|�@�@�\�̈ʁ@�@�|�@�@��̈�
�P�W�i�R�C�U�C�X�j�|�Q�O�i�T�C�V�C�W�j�|�V�i�P�C�Q�C�S�j�E�E�E(2)�̂P
�@�@���R�T�P�{�U�V�Q�{�X�W�S���Q�O�O�V
�@�@���U�T�P�{�R�V�Q�{�X�W�S���Q�O�O�V�E�E�E�������D
�P�W�i�R�C�V�C�W�j�|�Q�O�i�T�C�U�C�X�j�|�V�i�P�C�Q�C�S�j�E�E�E(2)�̂Q
�@�@���R�T�P�{�V�U�Q�{�W�X�S���Q�O�O�V
�@�@���V�T�P�{�R�U�Q�{�W�X�S���Q�O�O�V
�P�W�i�T�C�U�C�V�j�|�Q�O�i�R�C�W�C�X�j�|�V�i�P�C�Q�C�S�j�E�E�E(2)�̂R
�@�@���T�R�P�{�U�W�Q�{�V�X�S���Q�O�O�V
�@�@���U�R�P�{�T�W�Q�{�V�X�S���Q�O�O�V�E�E�E�������D
�P�X�i�Q�C�W�C�X�j�|�X�i�P�C�R�C�T�j�|�P�V�i�S�C�U�C�V�j�E�E�E(3)�̂P
�@�@���Q�P�S�{�W�R�U�{�X�T�V���Q�O�O�V
�@�@���W�P�S�{�Q�R�U�{�X�T�V���Q�O�O�V�E�E�E�������D
�P�X�i�R�C�V�C�X�j�|�X�i�P�C�Q�C�U�j�|�P�V�i�S�C�T�C�W�j�E�E�E(3)�̂Q
�@�@���R�P�S�{�V�Q�T�{�X�U�W���Q�O�O�V
�@�@���V�P�S�{�R�Q�T�{�X�U�W���Q�O�O�V�E�E�E�������D
�P�X�i�S�C�U�C�X�j�|�X�i�P�C�R�C�T�j�|�P�V�i�Q�C�V�C�W�j�E�E�E(3)�̂R
�@�@���S�P�Q�{�U�R�V�{�X�T�W���Q�O�O�V
�@�@���U�P�Q�{�S�R�V�{�X�T�W���Q�O�O�V�E�E�E�������D
�P�X�i�S�C�V�C�W�j�|�X�i�P�C�Q�C�U�j�|�P�V�i�R�C�T�C�X�j�E�E�E(3)�̂S
�@�@���S�P�R�{�V�Q�T�{�W�U�X���Q�O�O�V
�@�@���V�P�R�{�S�Q�T�{�W�U�X���Q�O�O�V�E�E�E�������D
�P�X�i�S�C�V�C�W�j�|�X�i�P�C�R�C�T�j�|�P�V�i�Q�C�U�C�X�j�E�E�E(3)�̂T
�@�@���S�P�Q�{�V�R�U�{�W�T�X���Q�O�O�V
�@�@���V�P�Q�{�S�R�U�{�W�T�X���Q�O�O�V�E�E�E�������D
�P�X�i�T�C�U�C�W�j�|�X�i�Q�C�R�C�S�j�|�P�V�i�P�C�V�C�X�j�E�E�E(3)�̂U
�@�@���T�Q�P�{�U�R�V�{�W�S�X���Q�O�O�V
�@�@���U�Q�P�{�T�R�V�{�W�S�X���Q�O�O�V�E�E�E�������D
�P�X�i�S�C�V�C�W�j�|�P�O�i�P�C�R�C�U�j�|�V�i�O�C�Q�C�T�j�E�E�E(4)�̂P
�@�@���S�P�O�{�V�R�Q�{�W�U�T���Q�O�O�V
�@�@���V�P�O�{�S�R�Q�{�W�U�T���Q�O�O�V�E�E�E�������D
�P�X�i�S�C�V�C�W�j�|�P�O�i�Q�C�R�C�T�j�|�V�i�O�C�P�C�U�j�E�E�E(4)�̂Q
�@�@���S�Q�O�{�V�R�P�{�W�T�U���Q�O�O�V
�@�@���V�Q�O�{�S�R�P�{�W�T�U���Q�O�O�V�E�E�E�������D
�P�X�i�T�C�U�C�W�j�|�P�O�i�O�C�R�C�V�j�|�V�i�P�C�Q�C�S�j�E�E�E(4)�̂R
�@�@���T�O�P�{�U�R�Q�{�W�V�S���Q�O�O�V
�@�@���U�O�P�{�T�R�Q�{�W�V�S���Q�O�O�V�E�E�E�������D
�P�X�i�T�C�U�C�W�j�|�P�O�i�P�C�Q�C�V�j�|�V�i�O�C�R�C�S�j�E�E�E(4)�̂S
�@�@���T�P�O�{�U�Q�R�{�W�V�S���Q�O�O�V
�@�@���U�P�O�{�T�Q�R�{�W�V�S���Q�O�O�V�E�E�E�������D
�����������g��Ȃ��悤�ɂ���A���ꂼ��̈ʂ̐����͏c�ʒu�Ŏ��R�ɓ�������̂ŁA
�@�@�@�R�T�P�@�@�@�@�U�T�P
�@�@�@�U�V�Q�@�@�@�@�R�V�Q
�@�@�{�X�W�S�@���@�{�X�W�S
�@�@�Q�O�O�V�@�@�@�Q�O�O�V
�ƌ�����ɉ��ʂ���l������Ǝv���܂��B
���ƁA�u���ʂ肠��̂��v���l���܂����B���܂莩�M�͂���܂��A
��L�̑g�ݍ��킹���ƂɂR�U�i�U�~�U�j�ʂ�A�P�R�̑g�ݍ��킹�ŁA
�S�U�W�ʂ�A�����̓����ʒu��������Ƃ����l���ɓ����ƁA
�Q�P�U�i�U�~�U�~�U�j�ʂ�A�P�R�̑g�ݍ��킹�ŁA�Q�W�O�W�ʂ�ł��傤���B
�E����11
�i�y���l�|���F�e���X�ƃA���X�j
�܂��A��̈ʂ��V�ɂȂ�R�̐����̑g�ݍ��킹���l���܂��B
�@�i0�A1�A6�j�i0�A2�A5�j�i0�A3�A4�j�i0�A8�A9�j
�@�i1�A2�A4�j�i1�A7�A9�j�i2�A6�A9�j�i2�A7�A8�j
�@�i3�A5�A9�j�i3�A6�A8�j�i4�A5�A8�j�i4�A6�A7�j
���̂P�Q�g���l�����܂��B
���̂����A
�i0�A8�A9�j�̏ꍇ��
�a���P�V�ɂȂ�A�\�̈ʂɂP�J��オ��܂��B
�c��1�`7�̂����̂R�̐����̘a�ōő�l�͂P�W�ƂȂ�܂��B
����ď\�̈ʂ̂R�̐����̘a�͂X�łȂ���Ȃ�܂���B
����ɕS�̈ʂɂP�J��オ��܂��B
����ĕS�̈ʂ̂R�̐����̘a�͂P�X�łȂ���Ȃ�Ȃ��̂ŁA
�v�Z���͐������܂���B
�i3�A6�A8�j�̏ꍇ��
�a���P�V�ɂȂ�A�\�̈ʂɂP�J��オ��܂��B
����ď\�̈ʂ̂R�̐����̘a�̈�̈ʂ͂X�łȂ���Ȃ�܂���B
�i0�A2�A7�j�Ɓi0�A4�A5�j�̓�g���l�����܂��B
����ɕS�̈ʂɂP�J��オ��܂��B
����ĕS�̈ʂ̂R�̐����̘a�͂P�X�łȂ���Ȃ�Ȃ��̂ŁA
�v�Z���͐������܂���B
����ȊO�ɂ��Ă͌v�Z���͐������܂��B
�i�P�j��̈ʂ��i0�A1�A6�j�̎��A
�@�@�\�̈ʂ́i2�A3�A5�j�ŁA�S�̈ʂ́i4�A7�A8�j�ł��B
�i�Q�j��̈ʂ��i0�A2�A5�j�̎��A
�@�@�\�̈ʂ́i1�A3�A6�j�ŁA�S�̈ʂ́i4�A7�A8�j�ł��B
�i�R�j��̈ʂ��i0�A3�A4�j�̎��A
�@�@�\�̈ʂ́i1�A2�A7�j�ŁA�S�̈ʂ́i5�A6�A8�j�ł��B
�i�S�j��̈ʂ��i1�A2�A4�j�̎��A
�@�@�\�̈ʂ́i0�A3�A7�j�ŁA�S�̈ʂ́i5�A6�A8�j�ł��B
�i�T�j��̈ʂ��i1�A2�A4�j�̎��A
�@�@�\�̈ʂ́i3�A8�A9�j�ŁA�S�̈ʂ́i5�A6�A7�j�ł��B
�i�U�j��̈ʂ��i1�A2�A4�j�̎��A
�@�@�\�̈ʂ́i5�A6�A9�j�ŁA�S�̈ʂ́i3�A7�A8�j�ł��B
�i�V�j��̈ʂ��i1�A2�A4�j�̎��A
�@�@�\�̈ʂ́i5�A7�A8�j�ŁA�S�̈ʂ́i3�A6�A9�j�ł��B
�i�W�j��̈ʂ��i1�A7�A9�j�̎��A
�@�@�\�̈ʂ́i2�A3�A4�j�ŁA�S�̈ʂ́i5�A6�A8�j�ł��B
�i�X�j��̈ʂ��i2�A6�A9�j�̎��A
�@�@�\�̈ʂ́i1�A3�A5�j�ŁA�S�̈ʂ́i4�A7�A8�j�ł��B
�i10�j��̈ʂ��i2�A7�A8�j�̎��A
�@�@�\�̈ʂ́i1�A3�A5�j�ŁA�S�̈ʂ́i4�A6�A9�j�ł��B
�i11�j��̈ʂ��i3�A5�A9�j�̎��A
�@�@�\�̈ʂ́i1�A2�A6�j�ŁA�S�̈ʂ́i4�A7�A8�j�ł��B
�i12�j��̈ʂ��i4�A5�A8�j�̎��A
�@�@�\�̈ʂ́i1�A2�A6�j�ŁA�S�̈ʂ́i3�A7�A9�j�ł��B
�i13�j��̈ʂ��i4�A6�A7�j�̎��A
�@�@�\�̈ʂ́i1�A3�A5�j�ŁA�S�̈ʂ́i2�A8�A9�j�ł��B
�����@�v�Z���͏�L�i1�j�`�i13�j�̐����̑g�ݍ��킹�łł��鎮�i468�ʂ�j�B
�g��Ȃ������́i1�j�`�i4�j�̎��́u9�v�A�i5�j�`�i13�j�̎��́u0�v
�E����12
�i�y���l�|���F�r�h�f�j
�O������`�F�O����X�܂ł̐��l�̑��a���X�~�P�O���Q���S�T
�O������a�F�R�̐��������ő�l���X�{�W�{�V���Q�S
�O������b�F�R�̐��������ŏ��l���O�{�P�{�Q���R
���̎�
�@�@���@���@��
�@�@���@���@��
�{�@���@���@��
------------------
�@�Q�O�@�O�@�V
�ɂ����āA���F���{���{�����V�܂��͂P�V
�@�@�i�O������a���Q�S�ȉ��Ŗ������V�ł��鐔�j
���F���{���{�����P�O�܂��͂Q�O�܂��͂X�܂��͂P�X
�@�@�i�O������a�E�b���R�ȏ�Q�S�ȉ��̐��ł���A�J�オ��P�����蓾��j
���F���{���{�����Q�O�܂��͂P�X�܂��͂P�W
�@�@�i�O������a���Q�S�ȉ��̐��ł���A�J�オ��P�܂��͂Q�����蓾��j
����ɁA�O������`���A���{���{���͂S�T�ȉ��łȂ���Ȃ�Ȃ��̂ŁA ��L�̎�蓾��g�ݍ��킹��
�@���@�@���@�@�� ------------------ �P�X�@�P�O�@�@�V....�p�^�[���i�P�j �P�W�@�Q�O�@�@�V....�p�^�[���i�Q�j�̂Q�ʂ�B
�@�ҎҒ��j�����ɍ����g�ݍ��킹�́A�R�p�^�[������܂��B
�p�^�[���i�P�j�̏ꍇ�A
�@�@�P�X�{�P�O�{�V���R�U���A�O������`�i���S�T�j�Ƃ̍��͂X�B
�p�^�[���i�Q�j�̏ꍇ�A
�@�@�P�W�{�Q�O�{�V���S�T���A�O������`�i���S�T�j�Ƃ̍��͂O�B
����āA�]��\�������鐔�l�͂X�ƂO�̂Q�B
���Ƃ́A�����������邩������Ηǂ��B
�p�^�[���i�P�j
�@�@�S�@�Q�@�O
�@�@�V�@�R�@�P
�{�@�W�@�T�@�U
------------------
�@�Q�O�@�O�@�V
�ȂǁB
�p�^�[���i�Q�j
�@�@�R�@�T�@�P
�@�@�V�@�U�@�Q
�{�@�W�@�X�@�S
------------------
�@�Q�O�@�O�@�V
�ȂǁB�y�z�X�ƂO
�E����13
�i�y���l�|���F�}�E���V�I�E�V���[�O���j
3���ڂ̑��a��20�ł͂Ȃ����Ƃ͖��炩�i�ڂ̑��a��0�ɂȂ��Ă��܂�����j�ł���B
�����3���ڂ̑��a��18��19�ł���B�i17�ȉ��̏ꍇ�A2���ڂ̑��a��30�ȏ�ɂȂ��Ă��܂�����j
������3���ڂ̑��a��18�ɂ��Ă����A3���ڂ̑��a+2���ڂ̑��a+1���ڂ̑��a�i���̐���A�Ƃ����j���i���j45�����藧�i�g������
0����9�܂ł̂����ꂩ8�R������A�̍ō��l��1�`9�̑��a�ł���45�j�̂�A��45���Ȃ��悤�ɁA2���ڂ̐��A1���ڂ̐������߂Ȃ���Ȃ�Ȃ��B
2���ڂ�20��19�ł��邪19�ɂ����1���ڂ̑��a��17�ɂȂ��Ă��܂�A�l��45���Ă��܂�����2���ڂ̑��a��20�ł���B������1���ڂ�7�ł���B
������A�l�����Ă݂��18+20+7=45������g��Ȃ�������0�ƕ�����B�����A���̏ꍇ�ǂ�Ȑ������Ă�
2007�ɂȂ�Ȃ��̂ł���B
�c����3���ڂ̑��a��19�̂Ƃ��ɂ��āB2���ڂ̑��a��10��9�ł���B���̏ꍇ�̈ꌅ�ڂ̑��a��7��17�ł���B ���̂Ƃ���A�l��19+10+7=36 19+9+17=45�őO�҂̏ꍇ�g��Ȃ�����9�ŁA��҂̏ꍇ�g��Ȃ�����0�ƕ�����B ����ȊO�̃p�^�[���͐�ɂȂ��̂łƂ肠����������Ă݂�ƁA�O�҂�812+735+460=2007�Ō�҂�719+825+463=2007 �Ƃǂ�������藧���ߓ����́@�O�ƂX
�E����14
 �i�y���l�|���F��̂�������j
�i�y���l�|���F��̂�������j
�����@�@�g��Ȃ������͂O�ƂX�ł��B
�P�@�Q�@�R�@�S�@�T�@�U�@�V�@�W�@�X�@�O�@�̂P�O�̐����̒���
�Q�O�O�V�̍��v�ɂ��邽�߂ɂ͊e�ʂ̍��v�����̂悤�ɂȂ�܂��B
���P�����V�̏ꍇ�ƂP�V�̏ꍇ������܂��B
���̒ʂ�A�P�O�O�̈ʁA�P�O�̈ʁA�P�̈ʂ̏��Ԃŏ����ƁA
�@�@(1)�@�@�@�P�X�A�P�O�A�V
�@�@(2)�@�@�@�P�W�A�Q�O�A�V
�@�@(3)�@�@�@�P�X�A�X�A�P�V
�̂R�ʂ�ł�
����������̍��v���o����
�@�@(1) �P�X�{�P�O�{�V���R�U�@(2)�@�P�W�{�Q�O�{�V���S�T�@(3)�@�P�X�{�X�{�P�V���S�T
�łX�̔{���ɂȂ��Ă��܂��B
�����̂O�`�X�܂ł����v����ƁB
�@�@�P�O�~�i�X�{�O�j���Q���S�T
(1)�̏ꍇ�͂R�U�Ȃ̂�
�@�@�S�T�|�R�U���X
�g��Ȃ������͂X�ƂȂ�܂��B
(2)(3)�̏ꍇ�͂S�T�Ȃ̂�
�@�@�T�|�S�T���O�Ȃ̂�
�g��Ȃ������͂O�ƂȂ�܂��B
�v�Z��
(1)�̏ꍇ�̗�@�@�@�@�@�@�@�@�@(2)�̏ꍇ�̗�@�@�@�@�@�@�@�@�@(3)�̏ꍇ�̗�
�@�@�@�T�@�P�@�O�@�@�@�@�@�@�@�@�@�@�R�@�T�@�P�@�@�@�@�@�@�@�@�@�@�@�X�@�P�@�V
�@�@�@�U�@�Q�@�R�@�@�@�@�@�@�@�@�@�@�U�@�V�@�Q�@�@�@�@�@�@�@�@�@�@�@�W�@�R�@�S
�{�@�@�W�@�V�@�S�@�@�@�@�@�@�@�@�{�@�X�@�W�@�S�@�@�@�@�@�@�@�@�@�{�@�Q�@�T�@�U
----------------- ----------------�@�@�@�@�@�@�@----------------
�@�Q�@�O�@�O�@�V�@�@�@�@�@�@�@�@�Q�@�O�@�O�@�V�@�@�@�@�@�@�@�@�@�Q�@�O�@�O�@�V
�E����15
�i�y���l�|���FT_Tatekawa�j
10�̐��̘a�� 45 �ł��D
�S�̈ʁC�\�̈ʁC��̈ʂɕ������܂��D
�O�̈قȂ鐔�̘a�͍ŏ��� 0+1+2=3, �ő傪 7+8+9=24 �ł��D
�J��オ��͑傫���Ă� 2 ��������܂���D
�����ŕS�̈ʂ� 18, 19, 20 �̏ꍇ�ɕ����čl���܂��D
�S�̈ʂ� 18 �̏ꍇ�F
�\�̈ʂ̘a�� 20�C��̈ʂ̘a�� 7 ���ƁC
�@�@18+20+7 = 45
����Ďg��Ȃ����� 0�D
��̓I�ȗ�Ƃ��ẮA
7 = 1+2+4
18 = 5+6+7 = 3+7+8 = 3+6+9
20 = 3+8+9 = 5+6+9 = 5+7+8
�\�̈ʂ̘a�� 19�C��̈ʂ̘a�� 17 ���ƁC
�@�@18+19+17 = 54 �� 45
����̓_���ł��D
�S�̈ʂ� 19 �̏ꍇ�F
�\�̈ʂ̘a�� 9�C��̈ʂ̘a�� 17 ���ƁC
�@�@19+9+17 = 45
����Ďg��Ȃ����� 0�D
��̓I�ȗ�Ƃ��ẮA
17 = 3+5+9
9 = 1+2+6
19 = 4+7+8
�\�̈ʂ̘a�� 10�C��̈ʂ̘a�� 7 ���ƁC
�@�@19+10+7 = 36
����Ďg��Ȃ����� 9�D
��̓I�ȗ�Ƃ��ẮA
7 = 0+1+6
10 = 2+3+5
19 = 4+7+8
�S�̈ʂ� 20 �̏ꍇ�́C�\�̈ʂ̘a�� 0 �łȂ���Ȃ�Ȃ��̂�
�����ł��D
����Ďg��Ȃ����� 0 �� 9 �ł��D
�E����16
�i�y���l�|���F�]�ʔ����j

��L�̂悤�ɁA���ɃA���t�@�x�b�g�Ă͂߂�
0�`�X�̓��A�O�̐����̘a�͍ő��7+8+9=24�Ȃ̂�
��̈ʂɂ��ĉ\���̂�����̂́A �f�{�g�{�T=7�A17
����āA�\�̈ʂɂ��Ẳ\���́A �c�{�d�{�e���P�O�A�Q�O�A�X�A�P�X
����ɁA�S�̈ʂɂ��ẮA �`�{�a�{�b���P�X�A�P�W
����ɁA�`�`�T�̘a�͂O���g��Ȃ��A�P�{�Q�{�E�E�{�X���S�T���ő�
�����̏�������A��ӂ����g����������Ɖ��\�̒ʂ�B
�g��Ȃ������͂S�T�Ƃ̍��ɓ������̂ŁA���́A�O�܂��͂X�ł���B
| �g���� | A+B+C | D+E+F | G+H+I | �`�`�h�̘a | �g��Ȃ����� (�S�T�Ƃ̍�) |
|---|---|---|---|---|---|
| �P�[�X(1) | 19 | 10 | 7 | 36 | 9 |
| �P�[�X(2) | 18 | 20 | 7 | 45 | 0 |
| �P�[�X(3) | 19 | 9 | 17 | 45 | 0 |
�E����17
�i�y���l�|���F�O�p��K�j
�g��Ȃ����́C�O �� �X�B

�E����18
�i�y���l�|���F�e�������s�j
�����Ȃ�ȗ�������Ă܂��i���j
���{���{�����Q�O�O�V�i���A���A���͂R���̐����ŁA�����������d�����Ȃ��j�ƂȂ邽�߂ɂ͂܂��A
���A���A���̂��ꂼ��̊e���̐����𑫂��āA
�X�̔{���i�Q�{�O�{�O�{�V���X�����炩�ȁH�j�ɂȂ�Ȃ��Ⴂ���Ȃ��悤�ȋC�͂����ł����A����̍����Əؖ����C�}�C�`�킩��܂���B
�����A���̂悤�ȉ�������������ŁA���̏ؖ�����������Ƃ����Ȃ�A�Ȃ�Ƃ��ł��܂����̂ő����Ă��܂��܂��i���Ԃ��Ȃ��̂Łj(^^�U
�����́u�O�ƂX�v�ł��Ԃ��Ă�Ǝv���܂����A
���w�͓��������\�R�Ɏ���܂ł̌o�܂̕����d�v�ł�����ˁB
���ƕs�{�ӂł��B
�E����19
�i�y���l�|���F�^�ẴT���^�j
�Q�O�O�V�͂X�̔{���B�܂�A�g���X�̐����̘a�͂X�̔{���ɂȂ�Ȃ��Ƃ����� ���B�@�O����X�܂ł������ƂS�T�ƂȂ�B��������P�g��Ȃ��������ǂ��Ă����� �����ʂ��X�̔{���Ƃ������Ƃ͎g��Ȃ������̉\���Ƃ��Ă���̂͂͂O���X������ ����B
�E����20
�i�y���l�|���Fteki�j
�����@�@�O�A�X
��@
�㋎�@�ł��B
�Q�O�O�V�͂X�̔{���ł��̂ŁA�R�̐��͍��v���X�̔{���ł��B
�i�X�̔{���̔���@�́A�e���̐��𑫂��ĂX�Ŋ����邱�Ƃ������ł��B�j
�Ƃ���ŁA�O�`�X�̍��v�͂S�T�ł��̂ŁA�]�鐔�͕K���X�̔{���ƂȂ�܂��B
�O�`�X�̂����A�X�̔{���͂O�ƂX�ł��B
�������A���ۂɂł��邩�ǂ�������Ă݂��킯�ł͂Ȃ��̂ŁA�ǂ��炩��
�����g��Ȃ��Ɛ������Ȃ��\���͂���܂��B
�Ƃ肠�����A���̓����𑗂��Ă���������(^^;;
�E����21
�i�y���l�|���F�X���[�N�}���j
���Ė��ł����A�A�A �����P���ɍl���܂����B
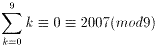
��������A1�����������Ă��A���̎������藧���߂ɂ́A
0��9�����Ȃ��B
���ۂɐ��������̓I�Ȑ����͕�����܂��B�B�B(^^;
�E����22
�i�y���l�|���Fkiyo�j
2007=9*223
ABC+DEF+GHI=9*223
A+B+C+D+E+F+G+H+1 (mod 9)
1+2+3+4+5+6+7+8+9=45=5*9 (mod 9)
0+1+2+3+4+5+6+7+8=36=4*9 (mod 9)
���������Ďg���Ȃ�����0��9�ł���B
���ۂQ�g�̏ꍇ�͍\�������B
�E����23
�i�y���l�|���F�m�Ɓ`�j
�ӂƗ��������WeekendMathematics�̍����̖��B
���̒��H���Z������
�̂͑�ς����ł����A�g���Ȃ�������T���̂͊ȒP�ł���ˁB
�Q�O�O�V���X�̔{��������A�O�`�X�̂����A��̘a���X�̔{���ɂȂ�
�悤�ɋ�I�ԂƁc�c�c�O���g��Ȃ����X���g��Ȃ����B
����H�K�v���͊ȒP������ǁA�\�����������ɂ͒��H���Z�������
�T���Ȃ��Ă͂Ȃ�Ȃ��H����ς�ʓ|�������Ȃ��B
�o�����Ă��܂��B
���Amail�𑗂��ēd������Ă���\�������������Ƃ��ł��܂����B
�����Ƃ����Ԃł����B
�@�@�@�O���g��Ȃ�
�@�@�@�@�@521+637+849�@�Ȃ�
�@�@�@�X���g��Ȃ�
�@�@�@�@�@420+731+856�@�Ȃ�
�E����24
�i�y���l�|���F�I���W�j
�i�P�j�Q�O�O�V�́A�e�ʂ̐��̘a���@�Q�{�O�{�O�{�V���X�@�ƂȂ�̂Ł@�X�̔{��
�i�Q�j�P�O�̐��̘a�@�O�{�P�{�Q�{�E�E�E�E�{�X���S�T ������@�X�̔{��
�]���ā@�P�O�̐��̂����@�P���̐����������A�X�̐��̘a���X�̔{���ƂȂ鐔�́A
�@�@�@�O�ƂX �E�E�i�Q�j�f
�������A�O�܂��͂X�������ĂX�̐��̘a���@�Q�O�O�V�@�Ɛ��邱�Ƃ��m���߂Ȃ��Ă͂Ȃ�Ȃ�
�����
�i�`�j�@�O���������ꍇ �i�a�j�X���������ꍇ
�@
�T�R�P �T�P�O
�U�W�Q �U�Q�R
�{ �@ �V�X�S �@ �{�@�W�V�S
------------- ------------
�Q�O�O�V �@ �Q�O�O�V�@
�i�Q�j�f�i�`�j�i�a�j����@�@���@�O�ƂX
�E����25
�i�y���l�|���F���܂����R�j�@�@�@�@�ꕔ�C��2/12
�P�̈ʂ��珇�ɑg�ݍ��킹��T���Ă������A���ӂ��Ǝv���o�����B
�R�̔{���y��9�̔{���́A���̐������\������e�ʂ̐��̘a��
���ꂼ��R�A�X�̔{���ɂȂ�A�Ƃ������Ƃ��B
2007��2+0+0+7=9�ƌ������Ƃ�9�̔{���B
�i�m�F�@2007��9=223�@�]��0�j
���Ȃ݂ɏ�̂X�̔{���̔���̏ؖ��́A
�@�@�@N=ax10n+.....+bx102 +cx10+d
�ɂ����āA10��1 (mod 9)����@10n��1 (mod 9)�ł���B
����āA
�@�@�@N��a+.....+b+c+d
�ƂȂ�AN��0 (mod 9)�ƂȂ�ɂ�
�@�@�@a+.....+b+c+d��0 (mod 9)
�łȂ���Ȃ�Ȃ��Ƃ������ƂɂȂ�B
�����̖��̎���
�@�@�@ax102 +bx10+c+dx102 +ex10+f+gx102 +hx10+i=2007��0 (mod 9)
a����i�ɂ͂��ꂼ��0����9�̂����ꂩ������A�d�����Ȃ��B
��̎����܂Ƃ߂��
�@�@�@(a+d+g)x102 +(b+e+h)x10+c+f+i��0 (mod 9)
���9�̔{���̔���̏ؖ�����
�@�@�@a+d+g+b+e+h+c+f+i��0 (mod 9)
����āA���ɓ���W�̐����̘a��9�̔{���ɂȂ��Ă���悢�B
���ɓ��肤�鐔����0����9�ł���B
�@�@�@0+1+2+3+4+5+6+7+8+9=45=9x5=(0+9)+(1+8)+(2+7)+(3+6)+(4+5)
���ɓ���鐔����8�ł���B
��̂Q�̐����̑g�ݍ��킹�̂���
���������Ȃ��Ȃ��Ă�9�̔{���̂܂܂Ȃ̂�
(0+9)�̑g�݂̂ł���B
����āA�����̖��̓����� 0��9�B
�E����26
�i�y���l�|���F��ӂ����̂炢��������j
���̖��̗v�_�́A2007��9�̔{�����Ƃ������Ƃł��B
�@�@�@2007��9�~223
0����9�܂ł̐������ׂč��v���Ă�9�̔{���ł��B
�@�@�@0�{1�{2�{3�{4�{5�{6�{7�{8�{9��45��9�~5
������A����10�̐�������P�����Ă��Ă�9�̔{���ɂȂ�̂́A�0�v���u9�v��������܂���B
a�`i��0����9�܂ł̐����̂ǂꂩ�Ƃ��܂��B
3���̐�abc�ɂ���
�@�@�@abc��a�~100�{b�~10�{c
�@�@�@�@��a�~(99�{1)�{b�~(9�{1)�{c
�@�@�@�@��9�~(11a�{b)�{(a�{b�{c)
�ƂȂ�̂ŁA�e�ʂ̐����̘a��9�̔{���Ȃ�Ό��̐���9�̔{���ł��B
���l�ɁA3�̐��ɂ���
�@�@�@abc�{def�{ghi��(a�{d�{g)�~(99�{1)�{(b�{e�{h)�~(9�{1)�{(c�{f�{i)
�@�@��9�~(11a�{11d�{11g�{b�{e�{h)�{(a�{b�{c�{d�{e�{f�{g�{h�{i)
�Ȃ̂Řa��2007�ɂȂ�3���̊e�ʂ̐����̘a��9�̔{���łȂ���Ȃ�܂���B

����9�́u���v�ɓ��鐔�������ׂĈقȂ肵�����a��9�̔{���ł���̂́A
�o0,1,2,3,4,5,6,7,8�p�܂���{1,2,3,4,5,6,7,8,9}�̂ǂ��炩�̏ꍇ�ł��B
�܂�A�u9�v���u0�v���g��Ȃ��ꍇ�ł��B
����ȊO�̏ꍇ�́A9�̔{���ɂȂ�܂���B
�ȉ���̓I�Ɋm�F���܂��B
- ��̈ʂ̐����̘a���u7�v�̂Ƃ�
(1)�\�̈ʂ̐����̘a���u10�v�̂Ƃ�(�S�̈ʂ̘a�u19�v)
�@a)��̈ʂɁu0�v����
�@�@* 0,9�̂ǂꂩ����������S�̈� �\�̈� ��̈� �a19 *(2,8,9) �a10 *(0,1,9) �a�V (0,1,6) �@ *(3,7,9) �@ *(0,2,8) �@ (0,2,5) �@ *(4,6,9) �@ *(0,3,7) �@ (0,3,4) �@ (4,7,8) �@ *(0,4,6) �@ �@ �@ (5,6,8) �@ (1,2,7) �@ �@ �@ �@ �@ (1,3,6) �@ �@ �@ �@ �@ (1,4,5) �@ �@ �@ �@ �@ (2,3,5) �@ �@
�\�ȑg�����A
�@�@(4,7,8), (2,3,5), (0,1,6)�@���u9�v�Ȃ�
�@�@(4,7,8), (1,3,6), (0,2,5)�@���u9�v�Ȃ�
�@�@(5,6,8), (1,2,7), (0,3,4)�@���u9�v�Ȃ�
�܂�A���ꂼ��̊��ʂ������Ƃ��ĎO�̐������Θa�����ׂ�2007�ł��B
�܂�A���ꂼ��̊��ʂ������Ƃ��ĎO�̐������Θa�����ׂ�2007�ł��B
��̑g�����ɑ��āA�O�̐��̏ꍇ�̐��͂R�U�ʂ�ł��B
�O���̏��Ԃ͖{���I�ł͂Ȃ��̂ŁA�S�̈ʂ̏��������ɕ��ׂĂ݂܂��B
�\�̈ʁA��̈ʂ͂��ꂼ��R�I�ʂ�ŕ��ׂ���̂ŁA�R�I�~�R�I���R�U�ʂ�ƂȂ�܂��B
�@b)��̈ʂɁu0�v�Ȃ�
�@�@*�@1,2,4�̂ǂꂩ����������S�̈� �\�̈� ��̈� �a19 *(2,8,9) �a10 *(0,1,9) �a�V (1,2,4) �@ **(3,7,9) �@ *(0,2,8) �@ �@ �@ *(4,6,9) �@ (0,3,7) �@ �@ �@ *(4,7,8) �@ *(0,4,6) �@ �@ �@ (5,6,8) �@ *(1,2,7) �@ �@ �@ �@ �@ *(1,3,6) �@ �@ �@ �@ �@ *(1,4,5) �@ �@ �@ �@ �@ *(2,3,5) �@ �@
�@�@**�@0,3,7�̂ǂꂩ���������
�\�ȑg�����A
�@�@(5,6,8), (0,3,7), (1,2,4)�@���u9�v�Ȃ�
(2)�\�̈ʂ̐����̘a���u20�v�̂Ƃ�(�S�̈ʂ̘a�u18�v)
�@a)��̈ʂɁu0�v����
�@�@*�@0,9�̂ǂꂩ����������S�̈� �\�̈� ��̈� �a18 *(1,8,9) �a20 *(3,8,9) �a�V (0,1,6) �@ *(2,7,9) �@ *(4,7,9) �@ (0,2,5) �@ *(3,6,9) �@ *(5,6,9) �@ (0,3,4) �@ **(3,7,8) �@ (5,7,8) �@ �@ �@ *(4,5,9) �@ �@ �@ �@ �@ **(4,6,8) �@ �@ �@ �@ �@ **(5,6,7) �@ �@ �@ �@
�@�@**�@5,7,8�̂ǂꂩ���������
�\�ȑg�����A
�@�@�Ȃ�
�@b)��̈ʂɁu0�v�Ȃ�
�S�̈� �\�̈� ��̈� �a18 *(1,8,9) �a20 (3,8,9) �a�V (1,2,4) �@ *(2,7,9) �@ *(4,7,9) �@ �@ �@ (3,6,9) �@ (5,6,9) �@ �@ �@ (3,7,8) �@ (5,7,8) �@ �@ �@ *(4,5,9) �@ �@ �@ �@ �@ *(4,6,8) �@ �@ �@ �@ �@ (5,6,7) �@ �@ �@ �@
�@�@*�@1,2,4�̂ǂꂩ���������
�\�ȑg�����A
�@(5,6,7), (3,8,9), (1,2,4)�@�� �u0�v�Ȃ�
�@(3,7,8), (5,6,9), (1,2,4)�@�� �u0�v�Ȃ�
�@(3,6,9), (5,7,8), (1,2,4)�@�� �u0�v�Ȃ�
- ��̈ʂ̐����̘a���u17�v�̂Ƃ�
(1)>�\�̈ʂ̐����̘a���u9�v�̂Ƃ�(�S�̈ʂ̘a�u19�v)
�@a)��̈ʂɁu0�v����
�S�̈� �\�̈� ��̈� �a19 (2,8,9) �a9 (0,1,8) �a17 *(0,8,9) �@ (3,7,9) �@ (0,2,7) �@ �@ �@ (4,6,9) �@ (0,3,6) �@ �@ �@ (4,7,8) �@ (0,4,5) �@ �@ �@ (5,6,8) �@ (1,2,6) �@ �@ �@ �@ �@ (1,3,5) �@ �@ �@ �@ �@ (2,3,4) �@ �@
�@�@* 0��9�����ɂ������
�\�ȑg�����A
�@�@�Ȃ�
b)��̈ʂɁu0�v�Ȃ�
�S�̈� �\�̈� ��̈� �a19 (2,8,9) �a9 (0,1,8) �a17 (1,7,9) �@ (3,7,9) �@ (0,2,7) �@ (2,6,9) �@ (4,6,9) �@ (0,3,6) �@ (2,7,8) �@ (4,7,8) �@ (0,4,5) �@ (3,5,9) �@ (5,6,8) �@ (1,2,6) �@ (3,6,8) �@ �@ �@ (1,3,5) �@ (4,5,8) �@ �@ �@ (2,3,4) �@ (4,6,7)
�\�ȑg�����A
�@(5,6,8), (2,3,4), (1,7,9)�@�� �u0�v�Ȃ�
�@(4,7,8), (1,3,5), (2,6,9)�@�� �u0�v�Ȃ�
�@(4,6,9), (1,3,5), (2,7,8)�@�� �u0�v�Ȃ�
�@(4,7,8), (1,2,6), (3,5,9)�@�� �u0�v�Ȃ�
�@(3,7,9), (1,2,6), (4,5,8)�@�� �u0�v�Ȃ�
�@(2,8,9), (1,3,5), (4,6,7)�@�� �u0�v�Ȃ�
(2)�\�̈ʂ̐����̘a���u19�v�̂Ƃ�(�S�̈ʂ̘a�u18�v)
a)��̈ʂɁu0�v����
�S�̈� �\�̈� ��̈� �a18 (1,8,9) �a19 (2,8,9) �a17 *(0,8,9) �@ (2,7,9) �@ (3,7,9) �@ �@ �@ (3,6,9) �@ (4,6,9) �@ �@ �@ (3,7,8) �@ (4,7,8) �@ �@ �@ (4,5,9) �@ (5,6,8) �@ �@ �@ (4,6,8) �@ �@ �@ �@ �@ (5,6,7) �@ �@ �@ �@
�@�@* 0��9�����ɂ������
�\�ȑg�����A
�@�@�Ȃ�(��0��9�͋��ɂ͂Ȃ�)
�@b)��̈ʂɁu0�v�Ȃ�
�S�̈� �\�̈� ��̈� �a18 (1,8,9) �a19 (2,8,9) �a17 (1,7,9) �@ (2,7,9) �@ (3,7,9) �@ (2,6,9) �@ (3,6,9) �@ (4,6,9) �@ (2,7,8) �@ (3,7,8) �@ (4,7,8) �@ (3,5,9) �@ (4,5,9) �@ (5,6,8) �@ (3,6,8) �@ (4,6,8) �@ �@ �@ (4,5,8) �@ (5,6,7) �@ �@ �@ (4,6,7)
�\�ȑg�����A
�@�@�Ȃ�
�\�ȑg�����́A�P�R�p�^�[������܂�����A�S���łP�R�~�R�U���S�U�W�ʂ�̐��̑g�ݍ��킹��������܂��B
�E����27
�i�y���l�|���FToru�j
�P
2007�͂X�̔{��������
�l�p�̒������ォ�牡��a,b,c,d,e,f,g,h,j�Ƃ����
�@�@�@100(a+d+g)+10(b+e+h)+c+f+j=9(11(a+d+g)+b+e+h)+a+b+c+d+e+f+g+h+j
���a+b+c+d+e+f+g+h+j��9�̔{���ł���K�v������B
����āA�g��Ȃ������Ƃ��čl��������̂́@0 or 9
0�̎����Ƃ��A351+762+894=2007
9�̎����Ƃ��A501+632+874=2007 �łǂ�����\�ł���B
���������ł�����S�����߂Ă݂悤�Ƃ̂��ƂŁA
�Q
�P�̈ʂ̘a�́@7 or 17
�P�̈ʂ̘a��7�̎��@�P�O�̈ʂ̘a�� 10 or 20
7,10 �̎��@�P�O�O�̈ʂ̘a�� 19
7,20�̎��@�P�O�O�̈ʂ̘a�́@18
�P�̈ʂ̘a��17�̎��@�P�O�̈ʂ̘a��9 or 19
17,9�̎��@ �P�O�O�̈ʂ̘a�́@19
17,19�̎��@�P�O�O�̈ʂ̘a�� 18
�ȏォ��A100�A10�A1�̈ʂ̘a�̑g�����Ƃ��Ă�
(19,10,7) (18,20,7) (19,9,17) (18,19,17)�̉\�������邪�Ō�̂��̂͑S�̘̂a
���T�S�ƂȂ��ĕs�\
(19,10,7)�̎��͂R�U������@9������
(18,20,7)�@(19,9,17)�̎��͂S�T���0������
�i�Ƃ������ƂŎg��Ȃ������Ƃ��čl��������̂�0��9�ɂȂ�܂��j
(19,10,7)�̎��@9��������
7��0+1+6,0+2+5,0+3+4,1+2+4�̂����ꂩ
19��4+7+8 or 5+6+8 �����������g��Ȃ��g�ݍ��킹�Ƃ��Ă�
(100�̈ʁA10�̈ʁA1�̈ʂ̏���)
(4+7+8,2+3+5, 0+1+6) (4+7+8,1+3+6, 0+2+5)
(5+6+8,1+2+7, 0+3+4) (5+6+8, 0+3+7,1+2+4)
(18,20,7)�̎��@0�������̂�
7��1+2+4 20��3+8+9,4+7+9,5+6+9,5+7+8�̂����ꂩ�@�����������g��Ȃ��g������
���Ă͓��l��
(5+6+7, 3+8+9, 1+2+4) (3+7+8,5+6+9,1+2+4) (3+6+9,5+7+8,1+2+4)
(19,9,17)�̎��@0�������̂�
9��1+2+6,1+3+5,2+3+4
19��2+8+9,3+7+9,4+6+9,4+7+8,5+6+8��
(2+8+9,1+3+5,4+6+7) (3+7+9,1+2+6,4+5+8) (4+6+9,1+3+5,2+7+8)
(4+7+8,1+2+6,3+5+9) (4+7+8,1+3+5,2+6+9) (5+6+8,2+3+4,1+7+9)
���ꂼ��ɂ��ĂP�i�ځA�Q�i�ځA�R�i�ڂ���ʂ��Ȃ����
(3!)2=36�ʂ�@��ʂ����(3!)3=216�ʂ肪�\�Ƃ������ƂɂȂ�܂��ˁB
������
�܂Ƃ�
����������̕��X����A�������������ǂ������肪�Ƃ��������܂����B
�����ɍ������̂�T���Ă����Ƃ������@������܂����A���̏ꍇ�A���ׂĂ�ԗ�����K�v������܂��ˁB
����ŁA�X�̏�](�X�Ŋ������Ƃ��̗]��)�ōl����ƁA�u�O�v�Ɓu�X�v
�ȊO�ɂ͂��肦�Ȃ��Ƃ������Ƃ��킩��܂��B
�������A���̏ꍇ���A�u�O�v���g��Ȃ��p�^�[���A�u�X�v���g��Ȃ��p�^�[����
�Ꭶ���邱�ƂŁA���̏\�����������K�v������Ǝv���܂��B
����ɖ����z���āA�����ɍ����g�ݍ��킹�͉��ʂ肠�邩�� �A�l�@���Ă���������������������Ⴂ�܂��B ���̑g�ݍ��킹�Ƃ��ẮA�P�R�p�^�[�����邩�Ǝv���܂��B ���̕��ו��ɂ��ẮA���Ԃ��l�����Ȃ���A�U�~�U���R�U�Ƃ���A�]���đS�̂Ƃ��ẮA �R�U�~�P�R���S�U�W�Ƃ���ɂȂ邩�ȂƎv���܂��B
 top
top