問題119　車の出迎え

１１９．車の出迎え

　X氏は、毎日定刻に駅に到着し、その時間ちょうどに着くよう家から迎えにきている車に乗って帰宅する。
　ある日、いつもより早い時間に駅に着いたX氏が家に向かって歩き始めたところ、途中のA地点で車とすれ違った。もし、この時点で車がX氏に気付いていれば、いつもより30分早く家に帰ることができたのであるが、あいにく車はX氏に気付かずに通り過ぎ、いつも通り駅に向かった。 X氏がA地点からさらに35分歩いたとき、駅に着いてすぐに引き返してきた車が追い付き、 X氏はそこから車に乗って、結局いつもと同じ時間に家に着いた。
　X氏の歩く速度と車の速度の比はいくらか。ただし、車の速度及びX氏の歩く速度は常に一定であり、車に乗り込む時間は無視できるものとする。

問題の出典

判断力を高める推理パズル
鈴木清士　著
講談社ブルーバックス
平成５年度国家公務員Ⅱ種試験

答えと解説

解答・その1

（ペンネ－ム：みけねこ）

＜解＞
Ｘ氏の歩く速さを：ｖ、車の速さを：Ｖ、駅からＡ地点までＸ氏が歩いた時間：ｔ、Ａ地点から３５分歩いた後に車に乗って家に着くまでの所要時間：Ｔ、Ａ地点から車に乗って家に着くまでの所要時間：Ｔ’、とすると、題意より以下の２式が成り立つ

　　　(1)：ｔ＋３５＋Ｔ＝ｔ＋Ｔ’＋３０
　　　(2)：ｖｔ＋３５ｖ＋ＶＴ＝ｖｔ＋ＶＴ’

(1)、(2)より

　　　Ｖ＝７ｖ

従って、車の速さは、Ｘ氏の歩く速さの７倍である。（終）

＜考察＞
答えが正しければ、一般に人の歩く速さは時速４～５ｋｍくらいだったと思うので車の速さは単純に考えると、時速２８～３５ｋｍになります。Ｘ氏の歩く速さが、一般よりも速いとしても車の速さはせいぜい時速４０ｋｍ弱であり、私の市内における制限速度は時速４０ｋｍ（他の地域は知りませんが…）なので車の運転手はかなり安全運転を心掛けているなぁと思ったのですが、制限速度を守って走る車はあまり無くむしろオーバーしていることが大半であると思うと、周りの状況にもよるのですが、この運転手にはもう少しスピードを出してもらいたいですね。（笑）まぁ、あまり移動手段に車を利用しない私にとっては無縁のことなんですけどね…

解答・その2

（ペンネ－ム：まーや）

（答え）１：７

駅から家までの距離をＳ（ｋｍ）、駅からＡ地点までの距離をＰ（ｋｍ）、Ａ地点から家までの距離をＱ（ｋｍ）とする。また、Ｘ氏の歩く速度をａ（ｋｍ/分）、車の速度をｂ（ｋｍ/分）とする。
いつもは、駅から車に乗りＳ/ｂ（分）で家に着く。
「ある日、いつもより早い時間に駅に着いたX氏が家に向かって歩き始めた」とあるので、いつもよりｃ分早く駅に着いてから、家に向かって歩き始めたとする。
途中のＡ地点で車がX氏に気付いていれば、いつもより30分早く家に帰ることができたので、

　　　Ｐ/ａ＋Ｑ/ｂ－ｃ＝Ｓ/ｂ－30　・・・（１）

となる。また、X氏がA地点からさらに35分歩いたとき、そこから車に乗って、結局いつもと同じ時間に家に着いたので、

　　　Ｐ/ａ＋35＋（Ｑ－35ａ)/ｂ－ｃ＝Ｓ/ｂ

となる。整理して、

　　　Ｐ/ａ＋35＋Ｑ/ｂ－35ａ/ｂ－ｃ＝Ｓ/ｂ　・・・（２）

(１)－(２)より

　　　－35＋35ａ/ｂ＝－30
　　　35ａ/ｂ＝５

両辺を35で割って

　　　ａ/ｂ＝１/７

よって、

　　　ａ：ｂ＝１：７

解答・その3

（ペンネ－ム：オヤジ）

d：駅から家までの距離
Ｔ：Ｘ氏の定刻の到着時刻
Ａ：通常より早く到着した分数
Ｂ：Ｘ氏がＡ地点まで歩いた分数
Ｖ：車の速度
Ｗ：Ｘ氏の歩く速度

１．Ｘ氏がＡ地点で車と出会った場合

　　　（Ｔ－ｄ／Ｖ）＋２×（ｄーＢＷ）／Ｖ＝Ｔ＋ｄ／Ｖー３０・・・（１）

２．車とＸ氏がＡ地点ですれ違った時刻

　　　（Ｔ－Ａ）＋Ｂ＝Ｔ－ｄ／Ｖ＋（ｄーＢＷ）／Ｖ　　　　　・・・（２）

３．Ｘ氏が、Ａ地点からさらに３５分歩いて車と出会った場合

　　　（Ｔ－Ａ）＋Ｂ＋３５＋｛ｄ－（Ｂ＋３５）Ｗ｝／Ｖ＝Ｔ＋ｄ／Ｖ・・（３）

（１）より　ＢＷ＝１５Ｖ　・・・（４）（２），（３）より

　　　　　（２Ｂ＋３５）Ｗ＝３５Ｖ　・・・（５）

（５）－（４）×２

　　　３５Ｗ＝５Ｖ　従って　Ｗ：Ｖ＝１：７

∴　Ｘ氏の速度：車の速度＝１：７

解答・その4

（ペンネ－ム：巷の夢）

通常時の駅から家までにかかる時間をT分、距離をL、X氏の分速度をｖ、車の分速度をV、ｔ　分早く着いたとし、歩き出し、自動車とすれ違った場所までの駅からの距離をｌ　とする。すると以下の二つの式が成立する。

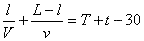　　　・・・・(1)

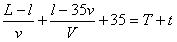　　　　・・・・・(2)
これらより T+t を消去すると、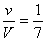となる。即ち、求めるものは1：7である。

解答・その5

（ペンネ－ム：スモークマン）

w 分早く駅につき、x 氏の速度をx、久留間の速度をy、家と駅の距離を z とすると、

　　　-w+30+(z-30x)/y=z/y-30
　　　-w+65+(z-65x)/y=z/y

から、

　　　35-35x/y=30

5/35=1/7=x/y となり、1：7　が答え。

解答・その6

（ペンネ－ム：のっこん）

Ｘ氏の歩く速さ・・分速a（m）　　車の速さ・・分速b（m）
駅からＡ地点まで・・ c（m) 駅から家まで・・ d（m）

　　　（2c+35a）÷b=35・・・(1)

Ａ地点で車とすれ違った時から時間を計ると
その　（c+d）÷b　分後がいつもの帰宅時間だから

　　　（c+d）÷b-（d-c）÷b=30・・・(2)

(1)、(2)より b=7a （答）１：７

解答・その7

（ペンネ－ム：にしやん）

回答：
家から駅までの距離をＬ、車の速度をＵ、Ｘ氏の歩く速度をＶとする。
駅からＡ地点までの距離をＭとすると、車が家からＡ地点まで行き、その後、家に戻った時にかかる時間は、

　　　２（Ｌ－Ｍ）／Ｕ

で表される。普段家から駅まで行き、また家に戻る時にかかる時間は、

　　　Ｌ／Ｕ

なので、

　　　（Ｌ－Ｍ）／Ｕ＋０．５＝２Ｌ／Ｕ

これより、

　　　Ｍ＝Ｕ／４・・・・・・ ① ３５分後、Ｘ氏はさらにＡ地点から

　　　３５Ｖ／６０

だけ家の方向に進むので、Ａ地点から車が３５分後に進む距離は、　　　２Ｍ＋３５Ｖ／６０

となる。従って

　　　３５Ｕ／６０＝２Ｍ＋３５Ｖ／６０

これより、

　　　Ｍ＝７（Ｕ－Ｖ）／２４・・・・・・ ②

①、②より

　　　Ｕ＝７Ｖ

従ってＸ氏の歩く速度と車の速度比は、１：７である。

解答・その8

（ペンネ－ム：meira）

x氏がいつもより速く駅に着いた時刻を0とおき，地点Aに着いた時刻をt_A，いつも自宅に着いていた時刻をt_Hとする。 x氏の歩く速さをv、車の速さをVとする。
地点Aで車に乗れば30分速く自宅についたのだから

　　　(駅から自宅までの距離)=　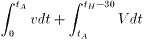　　…(1)

地点Aから35分歩いたところで車に乗っていつも通りの時刻についたのだから

　　　(駅から自宅までの距離)=　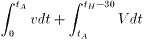　　…(2)

(1)=(2)より計算すると

　　　V=7v

よってx氏の歩く速さと車の速さの比はv:V

解答・その9

（ペンネ－ム：無鉄砲）

記述を簡略化するため、家=H 駅=S 地点A=A 車がX氏に追いついた地点=B と置く。また、車を基準とするため H-A-S-A-B-H となる線分を想定する。すると車は定時にHを出発し定時にHに戻る定速の運動をしているから、 AでX氏を乗せて戻った場合進む距離は(H-A)*2で、これは決められたコースよりも(A-S)*2だけ短い。これが車で30分の距離である。 Aを通過した車はSAを通ってBに進むが、これは(A-S)*2+(A-B) で、要した時間が35分。したがって(A-B)は車で5分に相当する。この距離をX氏は徒歩で35分かけているから (X氏の歩く速度):(車の速度)=1/35:1/5=1:7 …(答え)

ちなみに(A-S)*2=30より(A-S)=15 X氏の歩く速度に換算すると15*7=105 分となるので X氏は105+35=140分(2時間20分)だけ通常よりも早く駅に着いたことになる。

余計な考察：
線分置いたはいいけれど、解いてるときに視覚化が容易という以外にメリットはないことに気づきました。頭の中でも十分構成可能な問題内容なだけに答案としてはないほうが簡潔な部分だったようにも思います。それにしても歩くスピードを時速５Kmと仮定すると車の速度は35Km。いくら平均化したとはいえ、遅すぎだと思うのは私だけでしょうか？

解答・その10

（ペンネ－ム：MizuMimi）

Ａ地点で迎えの車とすれ違って、その時に車に乗れていれば３０分早く帰れたのだから、車で、Ａ地点から駅までの往復所要時間は３０分だと分ります。また、迎えの車はこの３５分後にＸ氏を乗せれたのだから、この地点をＢ地点とすると、Ａ地点からＢ地点までの車での所要時間は、３５分－３０分＝５分であったことが分かります。Ｘ氏はＡ地点からＢ地点まで３５分間歩き、その距離をＬ　歩いた速度をｓ(／分)とすると、

　　　Ｌ＝３５ｓ

この距離Ｌを車は５分で走ったのですから、車の速度をＳ(／分)とすると

　　　Ｌ＝３５ｓ＝５Ｓ

の関係式が成り立ちます。　よって、速これより度の比は　ｓ／Ｓ＝１／７

解答　Ｘ氏の歩く速度と車の速度の比は、１：７　です。

解答・その11

（ペンネ－ム：転位反応）

X氏はＡ地点から３５分間歩いた時、Ａ地点から車で帰宅する時の３０分間のゲインを失ったわけだから、X氏が３５分間で歩いた距離を車では５分間で走ることができる。よって、X氏の歩く速度：車の速度＝１：７である。

解答・その12

（ペンネ－ム：テレスとアリス）

「X氏がA地点からさらに35分歩いたとき、駅に着いてすぐに引き返してきた車が追い付いた」
このことから、Ａ地点から駅まで車で往復するのに30分かかることがわかります。さらにX氏に追いつくのに5分かかったことになります。 X氏が35分歩くところを、車で5分かかったので、 X氏の歩く速度と車の速度の比は、5対35、つまり、1対7となります。
答え　1対7

もしこれが正解であれば、駅からＡ地点までＸ氏は105分かけて歩き、さらに35分歩き、 140分（2時間20分）も歩いたことになる・・・そんなに歩くかナ？

解答・その13

（ペンネ－ム：ますますタコさん）

答え：　（歩き）１：（車）７

考え方：
問題文から、人の乗り降りや駅で方向転換する時間などは考えないで、純粋に『算数』の問題として、考えます。
最初に、X氏と車がすれ違った『A地点』で車の運転手がX氏に気が付いて家に向かっていれば、いつもより『３０分』早く家に着く（はず）ということは、この車で『A地点』から駅に向かい、再び『A地点』まで戻ってくるのに要する時間が『３０分』と言うことになります。
次に『A地点』からX氏が家に向かい、『３５分』歩いたときに復路の車と出合った。
同じ『３５分』を車の視点から見ると、X氏とすれちがった往路の『A地点』から復路の『A地点』を通過し、X氏に追いついた。
車は『A地点』から駅に向かい、再び『A地点』に戻るのが『３０分』だから、復路の『A地点』からX氏に出合うまでは『５分』となる。
つまり、それぞれ家に向かう（復路の）『A地点』から出合った場所までの所要時間は、 X氏が『３５分』、車が『５分』となります。
２者の速さの比は距離が同じ場合、かかった時間の比の逆数になるので、　（歩き）１：（車）７　となる。

余談になりますが、X氏は駅から『A地点』まで『１時間４５分』歩き、しかも駅から車に出合うまでにいたっては『２時間２０分』歩いたことになりますね・・・。

解答・その14

（ペンネ－ム：夜ふかしのつらいおじさん）

Ｘ氏の歩く速度と車の速度の比は、１：７です。

ＢをＸ氏が車に乗った地点とします。
Ｘ氏がいつもと同じ時間に家に着いたのは当然です。
車の動きを考えると、いつものように家を出ていつものように帰ってきました。
普段はＸ氏を、駅で乗せるのですが、ある日はＢ地点で乗せた違いがあるだけです。

Ａ地点でＸ氏が車に乗っていればいつもより３０分早く帰れたということは、車でＡ地点と駅を往復するのにかかる時間が３０分ということです。
Ｘ氏はＡ地点からＢ地点まで３５分で歩きました。車はＡ地点からＢ地点まで５分で走ることになります。

　Ｘ氏　　　＜１０５分＞　　　＜３５分＞
　　　駅---------------------Ａ-------Ｂ--～--～--～--家
　車　　　　　＜１５分＞　　　 ＜５分＞

Ｘ氏は車の７倍の時間がかかるので、Ｘ氏の歩く速度と車の速度の比は、１：７です。

なお、Ｘ氏は駅からＡ地点まで１０５分歩いたことになります。つまり駅からＢ地点まで１４０分歩いています。時速４Ｋｍとしても、１０Ｋｍ近く歩いています。（元気ですね）車は時速２８Ｋｍ程度です。（他の車の迷惑にならないのでしょうか）
また、これだけの条件ではあとどのぐらいで家に着くのかは分かりません。Ｘ氏は携帯電話を持っていなかったのでしょうか？

解答・その15

（ペンネ－ム：Toru）

A地点から駅までの往復に車で３０分かかるということだから、A地点からX氏が３５分で歩く距離を車は３５ー３０＝５（分）で走ったことになる。
従って速度の比は１：７

結局、車はいつものとおりの時間に家から駅を往復したわけですから、帰りつく時間が同じなのは当たり前ですね。

解答・その16

（ペンネ－ム：蜘蛛の巣城）

車が駅まで行き、引き返してきてX氏に追いついた所をB地点としましょう。

この問題のポイントは、車が普段通りに走っていることです。だから「結局いつもと同じ時刻に家に着いた」というのは当たり前で、ここは笑えました。こうした、なくもがなの文言に籠絡されるわけですね。
A地点とStationの往復に車で30分、さらにB地点まで5分。 X氏はA地点からB地点まで、35分かけて歩いています。
A地点からB地点まで、X氏と車の移動時間の比は７：１です。
従って、X氏の歩行速度と車の走行速度の比は１：７です。
のろのろ運転ですね。あるいはX氏が走るように歩くのか?

解答・その17

（ペンネ－ム：T_Tatekawa）

車が A 地点で X 氏を乗せていれば 30 分早く帰れる。しかし車は通り過ぎて駅に着き、戻ってきた。戻ってきた時刻は定刻なので、A 地点を再び車が通過するのは、最初に通過してから 30 分後。そして、車が X 氏に追いつくのはその 5 分後。 A 地点から X 氏が歩いていた時間は 35 分なので、X氏の歩く速さと車の速度の比は

　　　5 : 35 = 1 : 7

解答・その18

（ペンネ－ム：杖のおじさん）

答え　　１：７　です。
A地点（迎えに来た車とあった地点）で乗れば30分早く家に到着、B地点（駅まで行った車が戻って来た地点）で乗っていつもと同じ時間に到着したという事で次のように考えました。人がA地点からB地点まで３５分で歩き車に乗ったので車はA地点から駅まで行きA地点まで戻るのに往復３０分かかった事が分ります。従ってA地点で乗った場合に早く着いたと思う３０分がなくなり丁度の時間に家に着いた事になります。 35分―30分＝５分で車はA地点からB地点まで5分で走った事になりますので次の比が成り立ちます。

　　　人の時間：車時間＝３５分：５分＝７：１

従って　人の速度１に対して車の速度７となります。

解答・その19

（ペンネ－ム：teki）

答え　　１：７

この問題、方程式など使わなくても、問題の意味と車の動きが理解できていれば簡単に答えが出てきます。
A地点で車に乗れば、通常より３０分早く家に着くのですから、駅とA地点を車で往復するのに必要な時間は３０分です。 A地点から３５分歩いたところで車に乗り込むと通常と同じ時間に家に着くので、車がA地点から駅を経由して合流地点まで走るのに３５分かかることになります。よって、歩いて３５分の距離を車で５分で走った計算になるので、歩く速度と車の比は１：７です。

解答・その20

（ペンネ－ム：nao）

車がＡ地点まで往復するのと駅までを往復するのとで３０分差があるということは、Ａ地点と駅との間は、車で往復３０分の距離になります。
Ａ地点から家のほうまで３５分歩いたところをＢとすると、車はＡ地点から駅までいって折り返しＢ地点まで３５分かかったことになります。つまり、Ａ地点からＢ地点まで車は５分かかったということになります。それで、歩いて３５分のところを車は５分かかったことになるので、速さの比は１：７です。

解答・その21

（ペンネ－ム：ＦａｕｓＴ）

今回は「ダイヤ」を使って解いてみました。横軸に時間、縦軸に距離をとって鉄道なんかで用いられるアレです。直線の「傾き」が急なほど「速度が速い」とか、直線が「右上がりと右下がりでは進行方向が違う」とかが判ります。

今回おれが作ったダイヤ（図１）では「家が上で駅が下」としてますので、「右上がりの直線が『　駅　→　家　』」を表し、「傾きが緩やかな直線がＸ氏、傾きが急な直線が車」ということが言えます。

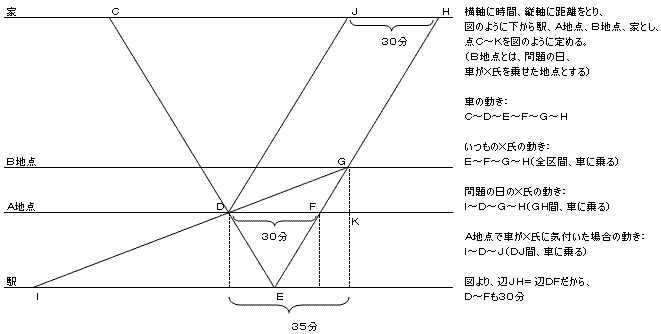
この図に、いつものＸ氏・車の動き、問題の日のＸ氏・車の動き等を直線で表し、題意にそって時間を決定すれば、２つの直線（Ｘ氏と車の速度）の関係が特定できます。

（図２）のようにＡ地点とＢ地点（問題の日、車がＸ氏を乗せた地点）の２点間の移動に要する時間を見ると、Ｘ氏が３５分、車が５分かかってます。

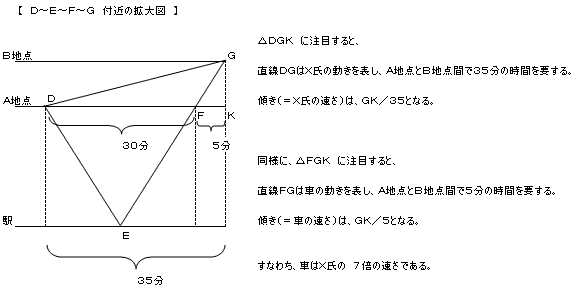
同距離間では時間と速さは反比例しますから、車の方が７倍速いと言えますね。よって、

Ｘ氏の速さ：車の速さ　＝　１：７　　・・・・・・【解】

　　　　　　　　　（　以　上　）

解答・その22

（ペンネ－ム：三角定規）

＜解答＞
題意より，この日のX氏および車のダイヤグラムは図のようになる。

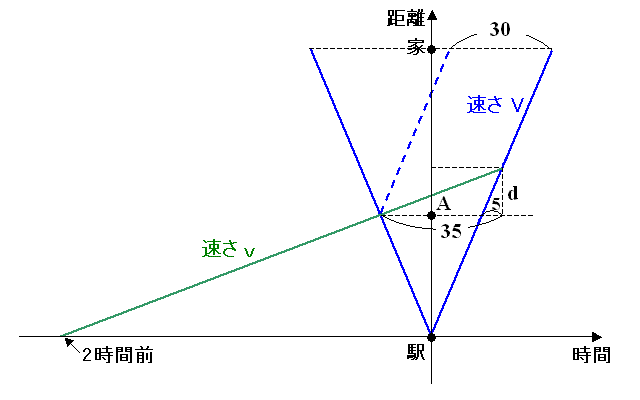
X氏，車の速さをｖ，V とし，A点から車に追いつかれた点までの距離をｄとすると，

　　　ｖ＝ｄ/３５，　V＝ｄ/（３５－３０）＝ｄ/５

　　　∴　ｖ： V＝ｄ/３５：ｄ/５＝５：３５＝１：７　…　［答］

＜感想＞
徒歩の平均速度は４ｋｍ/時程度ですから，これだと車の速さが２８ｋｍ/時程度となりいくらか遅いかなとも思いますが，駅そばの市街地は信号待ちやら渋滞やらも多いから，まあそんなものでしょうか。ただこの設定だと，X氏はいつもより２時間前に駅に着き，自宅に向かって２時間２０分も歩いた後に車に拾われているんですね。X氏の決意に脱帽です。

正解者

teki 無鉄砲巷の夢
オヤジにしやん Toru
nao 転位反応スモークマン
夜ふかしのつらいおじさんのっこん T_Tatekawa
テレスとアリスますますタコさんみけねこ
杖のおじさん meira MizuMimi
まーや蜘蛛の巣城三角定規
ＦａｕｓＴ

まとめ

Toruさんのご指摘にもあるように、車はいつも通りのコースをいつも通り走っただけですから、「結局いつもと同じ時間に家に着いた。」のは当たりまえですね。違うのは、Ｘ氏がどこで車に乗ったかということです。
問題文にある「この時点で車がＸ氏に気付いていれば、いつもより30分早く家に帰ることができた」ことから、「Ａ地点から駅まで車で往復するのに30分かかる」ということに着目すると、文字式を使わなくても、答えを求めることができますね。
三角定規さん、ＦａｕｓＴさんは、ダイヤグラムをかいてくださいました。電車の運行などを示すときに使われるものですね。
問題文の状況がやや（かなり？）現実離れしているというご指摘も受けましたが、数学の問題ゆえご勘弁を。駅から自宅が遠いとはいえ、毎日定刻に駅に到着し、そこから迎えの車で帰るというＸ氏が私にとってはかなりうらやましいです。皆さんはいかがですか？

Challenge!