侾侾俉丏儉乕價儞僌僂僅乕僋偺曕悢
俻墂偺峔撪偵偼摦偔曕摴乮儉乕價儞僌僂僅乕僋乯偑愝抲偟偰偁傞丅 俙巵偼晛抜側傜偙偺摦偔曕摴傪侾俆曕偱搉傞偑丄曕偔懍偝傪俀攞偵偡傞偲俀俆曕偱 搉傞偲偄偆丅 傕偟俙巵偑摦偔曕摴傪巊傢偢偵摨偠嫍棧傪曕偄偨偒偼丄壗曕偐偐傞偩傠偆偐丅 偨偩偟丄俙巵偺曕偔曕暆偼忢偵堦掕偱偁傞傕偺偲偡傞丅
栤戣偺弌揟
敾抐椡傪崅傔傞悇棟僷僘儖
楅栘惔巑丂挊
島択幮僽儖乕僶僢僋僗
暯惉14擭搙抧曽忋媺岞柋堳帋尡夵戣
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗傒偗偹偙乯
摎偊丗俈俆曕
亙夝亜
俙巵偺曕偔懍偝丗倴丄曕暆丟倶丄摦偔曕摴偺懍偝丗倁乫丄慡挿丗俴偲偡傞丅
傑偨丄偦傟偧傟偺強梫帪娫傪倲丄俿丄偲偡傞偲埲壓偺傛偆偵恾帵偱偒傞丅
丂丂丂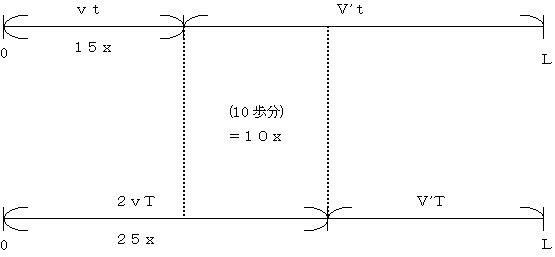
忋恾傛傝丄
丂丂丂(1)丂丗丂倁乫倲亅倁'俿亖侾侽倶
丂丂丂(2)丂丗丂倴倲丗俀倴俿亖侾俆倶丗俀俆倶
(1)丄(2)傛傝
丂丂丂倁'倲亖俇侽倶
備偊偵
丂丂丂倴倲亄倁'倲亖侾俆倶亄俇侽倶亖俈俆倶
埲忋傛傝
丂丂丂俈俆曕偐偐傞丅(廔)
夝摎丒偦偺2
乮儁儞僱亅儉丗僆儎僕乯
倓丗摦偔曕摴偺挿偝
俴丗俙巵偺曕暆
倁丗俙巵偺晛抜偺曕偔懍偝
俵丗摦偔曕摴偺懍搙
俽丗俙巵偺晛抜偺曕偔懍搙偱偐偐偨帪娫
俿丗俙巵偺晛抜偺曕偔俀攞偺懍搙偱偐偐偨帪娫
倓亖乮倁亄俵乯俽亖乮俀倁亄俵乯俿丒丒丒(1)
戣堄傛傝丂倁俽亖侾俆俴丆俀倁俿亖俀俆俴丒丒丒(2)
丂丂丂丂丂倁俽丗俀倁俿亖侾俆俴丗俀俆俴
丂丂丂丂丂俽丗俀俿亖俁丗俆丂傛傝丂俽丗俿亖俇丗俆
屘偵丂丂俽亖俇俿乛俆丒丒丒(3)
(1)傛傝丂倁俽亄俵俽亖俀倁俿亄俵俿丒丒丒(1)乫
(2)仺(1)乫丂侾俆俴亄俵俽亖俀俆俴亄俵俿
丂丂丂丂丂俵乮俽亅俿乯亖侾侽俴丒丒丒(4)
(3)仺(4)丂丂俵俿乛俆丂亖侾侽俴丂
丂丂丂丂丂俵俿亖俆侽俴丂丂丂丒丒丒(5)
(2)丆(5)仺(1)
丂丂倓亖乮俀倁亄俵乯俿亖俀倁俿亄俵俿
丂丂丂亖俀俆俴亄俆侽俴亖俈俆俴
丂丂亪俈俆曕
夝摎丒偦偺3
乮儁儞僱亅儉丗岼偺柌乯
摦偔曕摴偺挿偝傪L丄懍搙傪倁丄摓拝傑偱偺帪娫傪俿偲偡傞丅枖丄俙巵偺捠忢偺曕暆傪俙丄
晛捠偵曕偄偨帪偺摓拝帪娫傪俿1丄2攞偺懍搙偱曕偄偨帪偺摓拝帪娫傪
俿2偲偡傞偲戣堄傛傝埲壓偺曽掱幃偑惉傝棫偮丅
丂丂丂俴亅倁俿1亖侾俆俙丒丒丒丒丒(1)
丂丂丂俴亅倁俿2亖俀俆俙丒丒丒丒丒(2)
丂丂丂俴亖倁俿 丂丒丒丒丒丒丒丒丒(3)
偲偙傠偱丄嵟弶偲師偺懍搙斾偑2攞偱偁傞偐傜丄
丂丂丂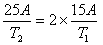
偑惉棫偡傞丅偙傟傛傝
丂丂丂俇俿1亖俆2丒丒丒丒丒(4)
場偭偰丄(1)丄(3)媦傃(4)傛傝倁俿1亖俇侽俙傪摼傞丅
偙傟傪(1)偵戙擖偡傞偲俴亖俈俆俙 傪摼傞丅
場偭偰偙偺嫍棧傪俙巵偺曕暆偱曕偔偲75曕傪梫偡傞丅
夝摎丒偦偺4
乮儁儞僱亅儉丗嶰妏掕婯乯
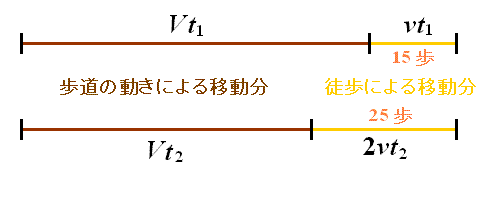
曕摴偑摦偔懍偝傪倁丆乮摦偔乯曕摴偵懳偟偦偺忋傪曕偔懍偝傪 v 偲偡傞丅
傑偨丆A巵偑捠忢曕摴忋傪曕偔帪娫傪 t1丆
2攞偺懍偝偱偁傞偔偲偒曕摴忋傪曕偔帪娫傪 t2 偲偡傞偲丆
曕悢亖嫍棧偺娭學乮佹曕暆偑曄傢傜側偄乯偐傜
丂丂丂倴t1 丗 2vt2亖侾俆 丗 俀俆
丂丂丂亪 t1 丗 t2亖俁侽 丗 俀俆 乧 嘆
曕摴偺挿偝偼曄傢傜側偄偺偩偐傜丆
丂丂丂乮倁亄倴乯倲1亖乮倁亄2倴乯倲2
丂丂丂亪 乮倁亄倴乯丒俁侽亖乮倁亄2倴乯丒俀俆
丂丂丂亪倁亖係倴丂丂亪丂乮倁亄v乯倲1亖5倴倲1
A巵偼 vt1 偺嫍棧傪 侾俆曕偱曕偔偺偩偐傜丆
5倴倲1 偺嫍棧偼 俈俆曕 偱曕偔丅乧乵摎乶丂丂仭
夝摎丒偦偺5
乮儁儞僱亅儉丗Mits乯
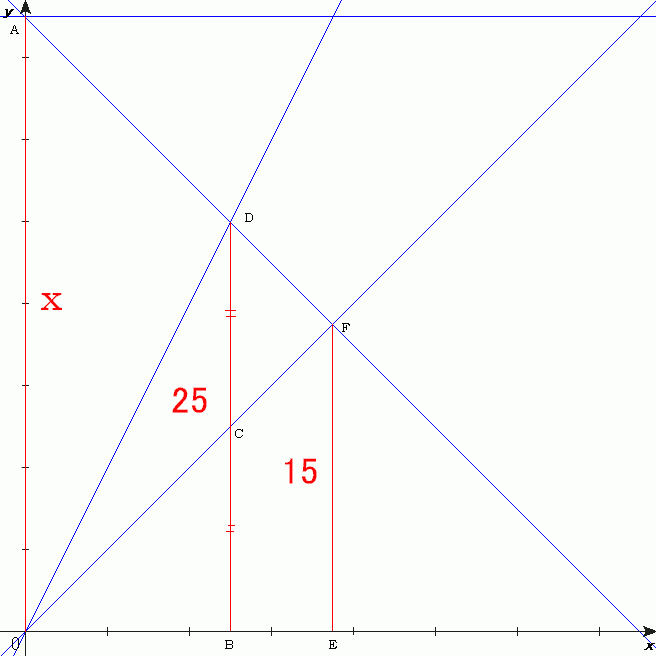
僌儔僼偵偍偄偰丄x幉偼帪娫丄y幉偼曕悢偱偁傝丄
捈慄OC丄OD丄AD偼偦傟偧傟y=v丄y=2v丄y=-v'+x乮v丗曕偔懍搙丄v'丗摦偔曕摴偺懍
搙丄x丗媮傔傞曕悢乯偱偁傞丅
栤戣偺忦審傛傝丄BD=25丄EF=15丅BC=CD=12.5傛傝丄
丂丂丂OC:CF=12.5:(15-12.5)=5:1
丂丂丂12.5:x=1:6丂亪x=75
埲忋偵傛傝丄摎偊偼75曕丅
夝摎丒偦偺6
乮儁儞僱亅儉丗揮埵斀墳乯
摦偔曕摴偺懍搙傪倁丄俙巵偺曕偔懍搙傪倴丄摦偔曕摴偺挿偝傪俴偲偡傞偲丄
俙巵偑摦偔曕摴傪堏摦偡傞偺偵梫偡傞帪娫偼丄俴乛(倁亄倴)
偝傜偵丄偙偺帪娫偱俙巵偑摦偔曕摴忋傪曕偔嫍棧偼丄俴倴乛(倁亄倴)
俙巵偺曕暆傪倵偲偡傞偲丄侾俆曕偱曕偔嫍棧偲摍偟偄偙偲偐傜丄
丂丂丂俴倴乛(倁亄倴)亖侾俆倵丂丂丒丒丒(1)
摨條偵偟偰丄曕偔懍搙偑俀倴偺応崌丄
丂丂丂俀俴倴乛(倁亄俀倴)亖俀俆倵丂丂丒丒丒(2)
(1)丄(2)傪夝偄偰丄嘪亖俀侽丄倴亖俆
摦偔曕摴傪巊傢偢偵丄嫍棧俴傪曕暆倵偱曕偔偲丄曕悢偼俴乛倵側偺偱
(1)傑偨偼(2)偵嘪亖俀侽丄倴亖俆傪戙擖偟偰丄
丂丂丂俴乛倵亖俈俆曕
夝摎丒偦偺7
乮儁儞僱亅儉丗僥儗僗偲傾儕僗乯
堦曕偺懍搙傪俙丄摦偔曕摴偺懍搙傪俛偲偟傑偡丅
摦偔曕摴傪侾俆曕偱搉傞偙偲偐傜丄搉傝偒傞偺偵堏摦偟偨嫍棧偼丄
丂丂丂15乮俙丂+丂俛乯
丂丂丂15俙丂+丂15俛丂丒丒丒丂(1)
曕偔懍偝傪俀攞偵偡傞偲俀俆曕偱搉傞偙偲偐傜丄
丂丂丂12乮2俙丂+丂俛乯丂+丂乮2俙丂+丂俛乯亐2
丂丂丂25俙丂+丂12.5俛丂丒丒丒丂(2)
(1)偲(2)偐傜丄
丂丂丂25俙丂-丂15俙丂亖丂15俛丂-丂12.5俛
丂丂丂10俙丂亖丂2.5俛
丂丂丂4俙丂亖丂俛
(1)偵戙擖偟偰
丂丂丂15俙丂+丂15乮4俙乯丂亖丂75俙
(2)偵戙擖偡傞偲
丂丂丂25俙丂+丂12.5乮4俙乯丂亖丂75俙
摦偔曕摴傪巊傢偢偵摨偠嫍棧傪曕偄偨偒偼丄75曕偵側傝傑偡丅
摎偊丂75曕
夝摎丒偦偺8
乮儁儞僱亅儉丗傑偡傑偡僞僐偝傫乯
夝摎丗俈俆曕
夝朄乮偲尵偆偐峫偊曽丠乯丗
晛抜A巵偑儉乕價儞僌僂僅乕僋乮埲壓丄MW乯偵忔傝巒傔偰偐傜崀傝傞傑偱丂
侾俆丂曕偱曕偔偲偙傠傪攞偺懍偝偱曕偄偨傜丄忔傝巒傔偰偐傜崀傝傞傑偱丂俀俆丂曕曕偄偨丄
偲尵偆偙偲偼晛抜傛傝攞偺懍偝偱曕偄偨偲偒偺曽偑搉傝廔偊傞傑偱偺帪娫偑
丂丂丂俀俆乛乮侾俆亊俀乯丂亖丂俆乛俇
偵側偭偨偲偄偆偙偲偵側傞丅
偦偺帪娫嵎丂乮侾乛俇乯丂暘偵MW偑摦偔嫍棧偼A巵偺晛抜曕偄偰偄傞曕悢偲
攞偺懍偝偱曕偄偨偲偒偺曕悢偺嵎
丂丂丂俀俆丂亅丂侾俆丂亖丂侾侽
曕暘偲偄偆偙偲偵側傞偺偱丄
晛抜A巵偑MW偵忔傝巒傔偰偐傜崀傝傞傑偱偵MW偑摦偔嫍棧偼
丂丂丂侾侽丂亊丂俇丂亖丂俇侽
曕暘偲側傞丅偙傟偵晛抜A巵偑曕偔曕悢傪壛偊傞偲
丂丂丂俇侽丂亄丂侾俆丂亖丂俈俆
偲側傝丄MW傪巊傢偢丄
摨偠嫍棧傪曕偄偨偲偡傞偲丄丂俈俆丂曕偲側傞乮偼偢丒丒丒乯
夝摎丒偦偺9
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
摎偊偼俈俆曕偱偡丅
乽a乿乮俆曕暘丄敿妏乯偱俙巵偺曕偄偨嫍棧丄乽俛乿乮慡妏乯偱曕摴偺摦偄偨挿偝傪昞偡偙偲偵偟傑偡丅
崌寁偑偙偺曕摴偺挿偝慡懱傪昞偟傑偡丅
丂丂丂aaa俛俛俛俛俛俛丂丒丒丒乮恾侾乯
丂丂丂aaaaa俛俛俛俛俛丂丒丒丒(恾俀)
侾俆曕偱曕摴傪搉傞偺偵偐偐偭偨帪娫傪乽侾乿偲偟傑偡丅
偡傞偲丄攞偺懍偝偱曕偗偽乽侾乿偺帪娫偱俁侽曕恑傔傑偡丅
偟偐偟丄俀俆曕偟偐曕偄偰偄側偄偺偱偙偺偲偒搉傞偺偵偐偐傞帪娫偼丄俀俆乛俁侽亖俆乛俇偱偡丅
曕摴偺摦偄偨挿偝偺斾偼丄乮恾侾乯偲乮恾俀乯偱偼丄俇丗俆偱偡丅
偙偺曕摴偺摦偄偨挿偝斾偺乽侾乿偼丄曕悢偱偼俀俆亅侾俆亖侾侽曕暘偵摉偨傝傑偡丅
偩偐傜丄乮恾侾乯傪傕偲偵峫偊傞偲丄侾俆亄侾侽亊俇亖俈俆乮曕乯偲側傝傑偡丅
夝摎丒偦偺10
乮儁儞僱亅儉丗Toru乯
媮傔傞曕悢傪X偲偡傞丅曕悢傪嫍棧偺扨埵偺傛偆偵峫偊傟偽丄
A巵偑侾俆曕偱曕偄偨帪丄摦偔曕摴偼丂(X-15) 曕暘偺嫍棧傪摦偒丄
俀俆曕偱曕偄偨帪偼丂(X-25)曕暘偺嫍棧傪摦偄偨偙偲偵側傞丅
摦偔曕摴偺僗僺乕僪偼堦掕偲偡傟偽丄偙偺嫍棧偼偐偐偭偨帪娫偵斾椺偡傞偙偲偵側傝丄
15曕曕偔帪娫偲丄俀攞偺懍搙偱25曕曕偔帪娫偺斾偼丂15丗25/2丂偱偁傞偐傜偙傟傪摍
偟偄偲抲偄偰
丂丂丂(X-15)丗(X-25)=15丗25/2 偙傟偐傜X=75
摎偊丂俈俆曕
夝摎丒偦偺11
乮儁儞僱亅儉丗抴鍋偺憙忛乯
侾俆曕偱曕偄偨偲偒偲丄俀俆曕偱曕偄偨偲偒偺奺乆傪忬嫷俙丄忬嫷俛偲偄偆偙偲偵偟傑偟傚偆丅
忬嫷俙偲忬嫷俛偺偐偐偭偨帪娫偺斾傪妋擣偟傑偡丅
曕暆偼忢偵堦掕偩偐傜曕偄偨嫍棧偼曕悢偦偺傕偺偱傛偄偱偟傚偆丅懍偝傪倴丄俀倴偱偁傜傢偡偲
丂丂丂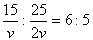
曕摴偑惷巭偟偨偲偒値曕偱曕偔傕偺偲偟丄摦偔曕摴偵塣偽傟偨嫍棧偲
曕摴偺懍偝兛偱忬嫷俙偲忬嫷俛偺偐偐偭偨帪娫偺斾傪偁傜傢偣偽
丂丂丂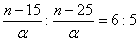
偙傟傛傝
丂丂丂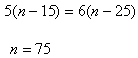
俈俆曕偱偟偨丅
夝摎丒偦偺12
乮儁儞僱亅儉丗偙傑偭偨僐偝傫乯
摦偔曕摴偺挿偝傪x倣偲偡傞丅
俙偝傫偺侾曕偺暆傪ym偲偟偰丄
俙偝傫偑捠忢偺懍偝乮侾俆曕偱曕摴傪搉傝偒傞偲偒偺曕偔懍偝乯偱
侾曕曕偔娫偵曕摴偑摦偔嫍棧傪zm偲偡傞丅
偡傞偲丄捠忢偺懍偝偱曕偄偨帪丄
丂丂丂x = 15(y+z)...(1)
偲側傞丅
堦曽丄俀攞偺懍偝偱曕偄偨偲偒偼
丂丂丂x = 25y + 25y/2
偲側傞丅
乮俙偝傫偑俀曕曕偄偨帪丄捠忢偺懍偝偺帪偺侾曕暘偩偗曕摴偑摦偄偰偄傞偙偲偵側傞丅乯
偙傟偱曽掱幃傪嶌傞偲
丂丂丂15(y+z) = 25y + 25y/2
丂丂丂30y + 30z = 50y + 25z
丂丂丂5z = 20y
丂丂丂z = 4y丂...(2)
傛偭偰俙偝傫偑捠忢偺懍偝偱侾曕曕偄偨帪丄
曕摴偼偦偺曕暆偺係曕暘恑傫偱偄傞偙偲偵側傞丅
曕摴傪巊傢偢偵曕偔偲偄偆偙偲偼
俙偝傫偼曕摴偑摦偄偰偄偨暘傕帺暘偱曕偔偙偲偵側傞丅
(2)傪(1)偵戙擖偟偰
丂丂丂X = 15(y+4y) = 75y
傛偭偰俙偝傫偑偙偺摦偔曕摴傪巊傢偢偵摨偠嫍棧傪帺暘偱曕偔偲俈俆曕偁傞偔偙偲偵側傞丅
夝摎丒偦偺13
乮儁儞僱亅儉丗namiusagi乯
摦偔曕摴偺嫍棧傪D偲偡傞丅
A巵偺曕暆傪W偲偟丄晛抜側傜偙偺摦偔曕摴傪15曕偱搉傞偺偱偙偺娫偵摦偔曕摴偺摦偔嫍棧傪a偲偡傞偲丄
丂丂丂D=a+15W乧乧乮侾乯
偵側傝傑偡丅
曕偔懍偝傪俀攞偵偡傞偲俀俆曕偱搉傞偺偱強梫帪娫偼晛抜偺25 /(15*2)亖 5/6偲側傞偺偱丄
偙偺娫偵摦偔曕摴偺摦偔嫍棧偼丄5a/6偵側傝丄
丂丂丂D=5a/6+25W乧乧乮俀乯
傪摼傑偡丅
(1)丄(2)偐傜a=60W偲側傝丄(1)幃傛傝D=75W偲側傞偺偱丄摦偔曕摴偺嫍棧偼A巵偺曕暆偺75攞丄偮傑傝俈俆曕暘偺嫍棧偵側傝傑偡丅
傛偭偰摎偼俈俆曕偱偡丅
夝摎丒偦偺14
乮儁儞僱亅儉丗T_Tatekawa乯
晛捠偺1曕偺娫偵曕摴偑恑傓嫍棧傪 x丆曕暆傪 y 偲偡傞丏
曕摴偺挿偝傪 L 偲偡傞丏
丂丂丂L = 15 (x+y) = 25 (x+y/2)
丂丂丂15 x+ 15 y = 25x + (25/2) y
丂丂丂10 x = 5/2 y
丂丂丂y = 4x
傛偭偰丆
丂丂丂L = 15 (x + 4x) = 75 x
摎偊丗75 曕
曕偔懍偝偺4攞偺懍偝偲偼丆憡摉懍偄乽摦偔曕摴乿偱偡偹丏
夝摎丒偦偺15
乮儁儞僱亅儉丗偺偭偙傫乯
MW忋傪傆偮偆偺儁乕僗偱曕偔帪偵偐偐傞帪娫偲
MW忋傪2攞偺儁乕僗偱曕偔帪偵偐偐傞帪娫偲偺斾偼
丂丂丂侾俆丗侾俀丏俆亖俇丗俆
廬偭偰丄
MW忋傪傆偮偆偺儁乕僗偱曕偔帪偺懍偝偲
MW忋傪2攞偺儁乕僗偱曕偔帪偺懍偝偺斾偼俆丗俇
A巵偑抧忋傪傆偮偆偺儁乕僗偱曕偔帪偺懍偝傪a
俵倂偦偺傕偺偺懍偝傪b偲偡傞偲
丂丂丂乮a+b乯丗乮2a+b乯亖5丗6
b=4a丂偲側傞偐傜丂a+b=5a
MW忋傪傆偮偆偺儁乕僗偱曕偔帪偺侾曕偼
抧忋傪傆偮偆偺儁乕僗偱曕偔帪偺俆曕偵偁偨傞偐傜
摎偼丂侾俆亊俆亖俈俆乮曕乯
夝摎丒偦偺16
乮儁儞僱亅儉丗俥倎倳倱俿乯
崱寧偼帪娫偑側偐偭偨偺偱丄偪傚偭偲嫮堷側峫偊偵側偭偰偟傑偄傑偟偨丄偡偄傑偣傫丅
曕悢埲奜偼悢抣偑梌偊傜傟偰側偄偺偱丄乽晛抜偺俙巵乿偺愝掕傪
侾曕丒侾倣丒侾昩丂偲彑庤偵寛傔傑偡丅
摦偔曕摴偺懍偝傪倶乮倣乛昩乯偲偡傟偽丄乽晛抜乿偼
丂丂丂乮侾亄倶乯亊侾俆丂丒丒丒偙傟偑曕摴偺挿偝偵側傝傑偡丅
曕偔懍偝傪乽俀攞乿偵偡傞偲丄
俀曕丒俀倣丒侾昩丂偲側傝傑偡偐傜丄
丂丂丂乮俀亄倶乯亊俀俆亐俀丂丒丒丒偙傟傕曕摴偺挿偝傪昞偟傑偡丅
忋婰俀幃傪夝偔偲丄
丂丂丂倶亖係
偑摼傜傟丄曕摴偺挿偝偼俈俆倣偲側傞丅丂
傛偭偰丄偙偺嫍棧傪俙巵偑曕偗偽俈俆曕梫偡傞偙偲偵側傞丅
丂丂丂俈俆曕丂丂丒丒丒丒丒丒亂夝亃丂丂
夝摎丒偦偺17
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂丂俈俆曕
恖偺懍搙A丄儉乕價儞僌僂僅乕僋偺懍搙傪B偲偟偰師偺幃偑惉傝棫偮丅
丂丂丂乮A+B乯丗乮俀A+B乯= 25/2丗15
偙偺幃偐傜A丂偲丂B丂偺斾傪寁嶼偡傞丅
丂丂丂A+B=25/2乧(1)仺A=25/2-B乧(2)
丂丂丂俀A+B=15乧(3)
(2)傪(3)偵戙擖
丂丂丂2(25/2-B )+B=15
丂丂丂25-2B+B=15
丂丂丂B=10乧(4)
(4)傪(3)偵戙擖
丂丂丂2A+10=15仺A=2.5乧(5)
廬偭偰丄A:B=侾丗係
恖偺懍搙侾偵懳偟偰儉乕價儞僌僂僅乕僋偺懍搙係偱偁傞丅
恖偼儉乕價儞僌僂僅乕僋偺懍搙係偲恖偺懍搙侾偺崌寁俆攞偺懍搙偱摦偄偰偄傞偺偱侾俆曕亊俆偱俈俆曕偱偡丅
夝摎丒偦偺18
乮儁儞僱亅儉丗teki乯
摎偊丂丂丂俈俆曕
夝朄
曽掱幃偱偡丅
偲尵偭偰傕丄枹抦悢偺抲偒曽偵彮偟擸傒傑偟偨丅
寢嬊丄摦偔曕摴偑晛捠偵曕偄偨偲偒偺堦曕傪曕偔娫偵恑傓嫍棧傪倶曕暘偲偟傑偟偨丅
乮偙傟偑堦斣偡傫側傝偟偨幃偵側傝傑偡丅乯
偱丄丂侾俆倶亄侾俆亖侾俀丏俆倶亄俀俆丂傪夝偄偰丄倶亖係
摦偔曕摴偺挿偝偼丄侾俆亊係亄侾俆亖侾俀丏俆亊係亄俀俆亖俈俆曕暘丂偲側傝傑偡丅
夝摎丒偦偺19
乮儁儞僱亅儉丗nao乯
傆偮偆偺懍偝偱堦曕曕偔偺偵侾昩偐偐傞偲偡傞偲丄侾俆曕偱拝偄偨偺偱侾俆昩偐偐偭
偨偙偲偵側傞丅擇攞偺懍偝偱偼丄堦曕曕偔偺偵(1/2)昩偱偡傓偺偱丄(25/2)昩偱拝
偄偨丅
曕摴偺挿偝傪侾偲偡傞偲丄侾俆昩偐偐偭偨偲偒偺懍偝偼(1/15)丄(25/2)昩偺帪偺
懍偝偼(2/25)丅偙傟偼偦傟偧傟丄
丂丂丂乮曕摴偺懍偝乯亄乮曕偔懍偝乯丄
丂丂丂乮曕摴偺懍偝乯亄乮俀攞偺曕偔懍偝乯
側偺偱丄
丂丂丂(2/25)-(1/15)=(1/75)
偼傆偮偆偺曕偔懍偝
偵側傞丅侾偺挿偝傪(1/75)偺懍偝偱曕偗偽丄俈俆昩偐偐傞丅堦曕曕偔偺偵侾昩偐偐傞偺偱丄
俈俆曕偱拝偔丅
亙峏側傞峫嶡亜
偙偺栤戣偼丄懍偔曕偄偨偺偵偳偆偟偰曕悢偑憹偊傞偺偩傠偆偲嶖妎偟傑偡丅
傕偟曕偐側偗傟偽丄曕悢偼僛儘丄曕偗偽偦偺暘偩偗曕悢偑憹偊傑偡丅偱偡偐傜丄懍偔
曕偔傎偳曕悢偑憹偊傞偙偲偵側傝偦偆偱偡丅
偦偙偱丄偳偆偄偆娭學偵側偭偰偄傞偐傪挷傋偰傒傑偟偨丅
曕悢偼丄堦曕傪扨埵偲偟偨摴偺傝偲傒側偡偙偲偑偱偒傑偡丅侾俆曕偱拝偄偨偲偒偺曕
偔懍偝傪倎丄曕摴偺懍偝傪倴丄曕摴偺挿偝傪倶偲偡傞偲丄倎偺懍偝偱侾俆偺摴偺傝傪
曕偔娫偵丄巆傝偺倶乕侾俆偺摴偺傝傪倴偺懍偝偱曕摴偑摦偔偙偲偵側傝傑偡丅偦偙偱丄
丂丂丂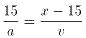 丂丂丒丒丒(1)
丂丂丒丒丒(1)
傑偨丄俀攞偺懍偝偱曕偔偲偒偼丄
丂丂丂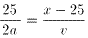 丂丂丒丒丒(2)
丂丂丒丒丒(2)
(1),(2)傪夝偄偰丄倶亖俈俆偑偱傑偡丅
偙偙偱丄忋偺幃傪嶲峫偵偟偰丄俙曕傪倎偱曕偒丄俛曕傪偦傟傛傝懍偄倐偱曕偄偨偲偡
傞偲丄
丂丂丂
偲偄偆俀偮偺幃偑偱偒丄懍偔曕偄偨曽偑懍偔拝偔偼偢側偺偱丄
丂丂丂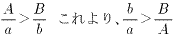 丂丂丂丒丒丒(3)
丂丂丂丒丒丒(3)
傑偨丄
丂丂丂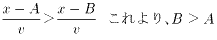 丂丂丂丒丒丒(4)
丂丂丂丒丒丒(4)
(3)偲(4)傛傝丄俛偺斖埻偼
丂丂丂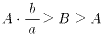
偱偁傞偙偲偑傢偐傝傑偡丅
偮傑傝丄懍偔曕偗偽丄偐側傜偢傕偲偺曕悢傛傝憹偊丄偨偲偊偽俀攞偺懍偝偱曕偗偽丄
傕偲偺曕悢偲偦偺俀攞偺曕悢偺娫偺曕悢偵側傞偙偲偑暘偐傝傑偟偨丅丂丂丂丂丂丂
惓夝幰
| 僆儎僕 | teki | nao |
| 栭傆偐偟偺偮傜偄偍偠偝傫 | 忨偺偍偠偝傫 | 揮埵斀墳 |
| 偺偭偙傫 | 岼偺柌 | Toru |
| 抴鍋偺憙忛 | 傑偡傑偡僞僐偝傫 | T_Tatekawa |
| namiusagi | 傒偗偹偙 | 偙傑偭偨僐偝傫 |
| Mits | 俥倎倳倱俿 | 僥儗僗偲傾儕僗 |
| 嶰妏掕婯 |
傑偲傔
巹偼嵟弶丄懍偔曕偔偺偵側偤曕悢偑憹偊傞偺偩傠偆丠丂偲慺杙偵巚偄傑偟偨丅
偦偆峫偊偨曽傕偄傜偭偟傖傞偺偱偼側偄偱偟傚偆偐丅傛偔傛偔峫偊偰傒傟偽丄
帪娫偑抁偔側傟偽丄摦偔曕摴偺壎宐傪庴偗傞検偑尭傝傑偡偐傜丄偦偆側傞偺偱偡傛偹丅
懡偔偺曽偑丄壗傜偐偺曽掱幃傪棫偰偰夝偄偰偔偩偝偭偰偄傑偡偑丄
斾偱峫偊傞偙偲偱丄曄悢偺悢傪尭傜偡偙偲偑偱偒傑偡丅
墶昹丄嶗栘挰偺墂偵傕摦偔曕摴偑偁傝傑偡丅
儔儞僪儅乕僋僞儚乕傗傒側偲傒傜偄抧嬫側偳
傪妝偟傒側偑傜丄堏摦偡傞偙偲偑偱偒傑偡丅
惀旕丄墶昹傊偍墇偟偺嵺偼偍棫偪婑傝偔偩偝偄丅
 top
top