Weekend Mathematics乛栤戣乛115椏嬥強偺栤戣
侾侾俆丏椏嬥強偺栤戣
崅懍摴楬偺椏嬥強偵挿偄幵楍偑偱偒偰偄偰丄偦偺屻傕枅暘侾俀侽戜偺妱崌偱丄 偙偺幵楍偺屻偵帺摦幵偑憹偊偰偄偔丅 椏嬥強偺僎乕僩傪係売強奐偔偲幵楍偼俁侽暘偱側偔側傝丄 俇売強奐偔偲幵楍偼侾俆暘偱側偔側傞偲偄偆丅 弶傔偺幵楍偵偼丄帺摦幵偑壗戜偁偭偨偐丅
戝恖偵栶棫偮嶼悢偺帪娫
庤搰彑楴丂娔廋
塱壀彂揦
夝摎丒偦偺1
乮儁儞僱亅儉丗僆儎僕乯
嵟弶偵倃戜幵偑偁偭偨偲偟傑偡丅
堦僇強偺椏嬥強偱丄枅暘俵戜傪捠夁偝偣傞偲偟傑偡丅
戣堄傛傝
丂丂丂俁侽亊係俵亖倃亄俁侽亊侾俀侽
丂丂丂侾俆亊俇俵亖倃亄侾俆亊侾俀侽
廬偭偰丂丂侾俀侽俵亖倃亄俁俇侽侽丂乮戜乯丒丒丒嘆
丂丂丂丂丂丂俋侽俵亖倃亄侾俉侽侽丂乮戜乯丒丒丒(2)
丂丂嘆乕(2)傛傝
丂丂丂丂丂丂俁侽俵亖侾俉侽侽
丂丂丂丂丂丂丂丂俵亖俇侽戜乛暘丒丒丒(3)
丂丂丂丂丂丂(3)傪(2)偵戙擖偟偰
丂丂丂丂丂俆係侽侽亖倃亄侾俉侽侽
丂丂丂丂丂丂丂丂倃亖俁俇侽侽
丂丂丂丂丂丂丂亪丂俁俇侽侽戜
夝摎丒偦偺2
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丄嵟弶偵暲傫偩幵偺憤悢偼仺俁俇侽侽戜偱偡丅
嵟弶偵暲傫偩幵偺憤悢傪Y偲偟偰丄侾偮偺僎乕僩偑捠偡侾暘娫偺張棟戜悢傪倸偲偡傞偲丅 師偺幃偑惉傝棫偪傑偡丅
係戜偺僎乕僩傪奐偗偨偲偒偺寁嶼偼師偺捠傝偱偡丅
丂丂丂Y+俁侽亊侾俀侽乗Z亊係亊俁侽亖侽乧(1)
俇戜偺僎乕僩傪奐偗偨偲偒偺寁嶼偼師偺捠傝偱偡丅
丂丂丂Y+侾俆亊侾俀侽乗Z亊俇亊侾俆亖侽乧(2)
(1)傪曄宍偡傞偲
丂丂丂Y亄俁俇侽侽亅侾俀侽Z亖侽 丂丂丂Y=侾俀侽Z亅俁俇侽侽乧(3)
(2)傪曄宍偡傞偲
丂丂丂Y亄侾俉侽侽亅俋侽Z亖侽乧(4)
(3)傪(4)偵戙擖偡傞偲
丂丂丂侾俀侽Z亅俁俇侽侽亄侾俉侽侽亅俋侽Z亖侽
丂丂丂俁侽Z=侾俉侽侽丂丂丂Z=俇侽乮戜乯乧(5)
(4)傪(3)偵戙擖偡傞偲
丂丂丂Y亖侾俀侽亊俇侽亅俁俇侽侽亖俈俀侽侽亅俁俇侽侽亖俁俇侽侽戜
偱偡丅
夝摎丒偦偺3
乮儁儞僱亅儉丗岼偺柌乯
嵟弶偺戜悢傪X丄僎乕僩偑張棟偡傞枅暘偺戜悢傪Y偲偡傞偲丄戣堄傛傝
丂丂丂X亄30亊120亖30亊Y亊4
丂丂丂X亄15亊120亖15亊Y亊6
偲側傞丅偙偺楢棫曽掱幃傪夝偄偰丄
丂丂丂Y亖60
丂丂丂X亖3600
場偭偰丄嵟弶偺戜悢偼3600戜丒丒丒丄偆乕傫乕丅
夝摎丒偦偺4
乮儁儞僱亅儉丗嶰妏掕婯乯
乻夝摎乼
巒傔偺廰懾戜悢傪 倶 戜丆僎乕僩侾儢強偺侾暘娫偁偨傝偺張棟戜悢傪 y 戜偲偡傞偲丆戣堄傛傝
丂丂丂倶亄侾俀侽亊俁侽亖侾俀侽倷丂乧乧嘆
丂丂丂倶亄侾俀侽亊侾俆亖丂俋侽倷丂乧乧嘇
嘆亅嘇丗丂俁侽倷亖侾俀侽亊侾俆丂丂亪丂倷亖俇侽丂乧乧嘊
嘊傪嘇偵戙擖偟偰丆丂倶亖俋侽亊俇侽亅侾俀侽亊侾俆亖俁丆俇侽侽
乵摎乶丂廰懾戜悢丂俁丆俇侽侽戜
夝摎丒偦偺5
乮儁儞僱亅儉丗namiusagi乯
摎偼3,600戜
弶傔偺幵楍傪X戜偲偟丄僎乕僩1儢強偺1暘偁偨傝偺 張棟擻椡傪a偲偡傞偲 僎乕僩4儢強偱偼丄
丂丂丂a=(X+120亊30)/4亊30 乧乧乮1乯
僎乕僩6儢強偱偼丄
丂丂丂a=(X+120亊15)/6亊15乧乧乮2乯
(1)=(2)傛傝丄
丂丂丂(X+120亊30)/4亊30=(X+120亊15)/ 6亊15
丂丂丂(X/120)+30=(X/90)+20
丂丂丂(4X/360)-(3X/360)=30-20
丂丂丂X=10亊360=3600
夝摎丒偦偺6
乮儁儞僱亅儉丗俥倎倳倱俿乯
嵟弶偺幵楍悢傪丂倶丂丄侾偮偺椏嬥強乮僎乕僩乯偑1暘娫偱張棟偡傞幵悢傪丂倷丂偲偡傞偲丄 師偺娭學幃偑摼傜傟傞丅
丂丂丂倣暘屻偺幵楍悢丗乮倶乮戜乯乯亄侾俀侽乮戜乯亊乮倣乮暘乯乯
僎乕僩傪値売強愝抲偟偨偲偒丄倣暘娫偵張棟偱偒傞幵悢丗
丂丂丂乮値乮売強乯乯亊乮倣乮暘乯乯亊乮倷乮戜乛暘乯乯
戣堄乮倣暘屻偵幵楍偑側偔側傞乯傪枮偨偡偵偼丄 乽暲傫偱偄傞幵楍悢乿偲乽張棟偡傞幵悢乿偑堦抳丄 偡側傢偪忋婰俀幃偑乽亖乮僀僐乕儖乯乿偲側偭偨帪偱偁傞丅
戣堄乮係売強愝偗傟偽俁侽暘偱張棟丄俇売強愝偗傟偽侾俆暘偱張棟乯傛傝丄 乮倣丆値乯亖乮俁侽丆係乯丆乮侾俆丆俇乯偺俀偮偺忦審傪丄忋弎偟偨娭學幃偵 偦傟偧傟摉偰偼傔傟偽丄壓婰偺偲偍傝倶丄倷偵偮偄偰偺楢棫曽掱幃偑摼傜傟傞丅
丂丂丂倶亄侾俀侽丒俁侽亖係丒俁侽丒倷
丂丂丂倶亄侾俀侽丒侾俆亖俇丒侾俆丒倷
偙傟傪夝偄偰丄
丂丂丂倶亖俁俇侽侽丄倷亖俇侽
栤戣偼丄嵟弶偺幵楍悢乮倶乯偺傒幙偟偰偄傞偺偱丄媮傔傞夝偼丄 俁俇侽侽丂乮戜乯丂丂丒丒丒丒丒丒亂夝亃丂丂丂偲側傞丅
夝摎丒偦偺7
乮儁儞僱亅儉丗偺偭偙傫乯
僎乕僩侾売強偺張棟擻椡傪侾暘偁偨傝a戜偲偡傞
係売強俁侽暘偱偼侾俀侽a戜傪張棟偡傞
俇売強侾俆暘偱偼俋侽a戜傪張棟偡傞
弶傔偺幵楍偵x戜偁偭偨偲偡傞偲
丂丂丂x亄侾俀侽亊俁侽亖侾俀侽a丒丒丒丒(1)
丂丂丂x亄侾俀侽亊侾俆亖俋侽a丒丒丒丒(2)
(1)丄(2)傛傝x亖俁俇侽侽乮戜乯
僯儏乕僩儞嶼偰傗偮偐側丠
夝摎丒偦偺8
乮儁儞僱亅儉丗teki乯
摎偊丂俁俇侽侽戜
亙夝朄亜丂擇尦楢棫曽掱幃
嵟弶偵暲傫偱偄偨幵偺戜悢傪倶丄僎乕僩侾偮摉傝偺侾暘娫偺捠夁戜悢傪倷偲偡傞偲丄
丂丂丂倶亄侾俀侽亊侾俆亖侾俆亊俇亊倷
丂丂丂倶亄侾俀侽亊俁侽亖俁侽亊係亊倷
偙傟傪夝偄偰丄倶亖俁俇侽侽丄倷亖俇侽丅
側偍丄僯儏乕僩儞嶼偵偼丄侾丗俀仺俀丗俁偵偡傞斾傪梡偄偨嶼悢夝朄偑偁傞傫偱偡偑丄 偙傟偼偳側偨偐偑昁偢彂偄偰偔傟傞偲巚偄傑偡偺偱丄徣棯偟傑偡丅
夝摎丒偦偺9
乮儁儞僱亅儉丗僥儗僗偲傾儕僗乯
亂夝摎亃
愝栤偐傜丄師偺幃偑惉傝棫偪傑偡丅
椏嬥強偺僎乕僩侾売強偱張棟偱偒傞戜悢傪俙偲偟傑偡丅
傑偨丄弶傔偺幵楍偺帺摦幵戜悢傪俛偲偟傑偡丅
椏嬥強偺僎乕僩傪係売強奐偔偲幵楍偼俁侽暘偱側偔側傞偙偲偐傜丄
丂丂丂俙丂亊丂30丂亊丂4丂亖丂120丂亊丂30丂+丂俛
椏嬥強偺僎乕僩傪俇売強奐偔偲幵楍偼侾俆暘偱側偔側傞偙偲偐傜丄
丂丂丂俙丂亊丂15丂亊丂6丂亖丂120丂亊丂15丂+丂俛
偦傟偧傟偺幃傪傑偲傔傞偲丄
丂丂丂120俙丂亖丂3600丂+丂俛
丂丂丂90俙丂亖丂1800丂+丂俛
偲側傝傑偡丅 偙傟傛傝丄
丂丂丂乮3600丂+丂俛乯丂懳丂乮1800丂+丂俛乯丂亖丂120丂懳丂90
偲側傞傛偆側俛傪媮傔傑偡丅
90乮3600丂+丂俛乯丂亖丂120乮1800丂+丂俛乯
324000丂+丂90俛丂亖丂216000丂+丂120俛
30俛丂亖丂108000
俛丂亖丂3600
摎偊丂3600戜
亂暿夝摎亃
椏嬥強偺僎乕僩傪係売強奐偔偲幵楍偼俁侽暘偱側偔側傞
椏嬥強偺僎乕僩傪俇売強奐偔偲幵楍偼侾俆暘偱側偔側傞
偲偺愝栤偐傜丄 椏嬥強偺僎乕僩俀売強偱丄侾俆暘娫偱丄
丂丂丂乮120丂亊丂15乯丂亖丂1800戜
張棟偱偒傞偙偲偵側傝傑偡丅俇売強偱丄侾俆暘娫偱
丂丂丂乮120丂亊丂15乯丂亊丂3丂亖丂5400戜
張棟偱偒偨偙偲偵側傝傑偡丅15暘娫偱偼丄
丂丂丂乮120丂亊丂15乯丂亖丂1800戜
憹偊偨偺偱丄弶傔偺幵楍偺帺摦幵戜悢偼丄
丂丂丂5400丂-丂1800丂亖丂3600戜
偲側傝傑偡丅
摎偊丂3600戜
夝摎丒偦偺10
乮儁儞僱亅儉丗Toru乯
侾俆暘屻傑偱偵屻曽偐傜棃傞幵偼120x15=1800 戜
俁侽暘屻傑偱偵屻曽偐傜棃傞幵偼120x30=3600 戜
弶傔偺幵楍偺戜悢傪x偲偡傟偽
丂丂丂(1800+x)丗(3600+x)=6x15丗4x30=3丗4
傛傝丂x=3600 摎偊丂3600戜
夝摎丒偦偺11
乮儁儞僱亅儉丗傂傠乯
弶傔偺幵偺悢傪x,侾儢強侾暘偁偨傝偵僎乕僩傪捠夁偡傞幵偺悢傪y偲偡傞丅
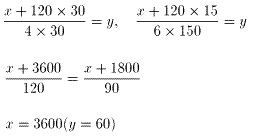
夝摎丒偦偺12
乮儁儞僱亅儉丗T_Tatekawa乯
弶傔偺帺摦幵偺戜悢傪 x 戜偲偡傞丅
4僇強偺僎乕僩偱偼30暘偱帺摦幵偑側偔側傝丄
6僇強偺僎乕僩偱偼15暘偱帺摦幵偑側偔側傞丅
1僇強偺僎乕僩偑1暘偵張棟弌棃傞帺摦幵偺悢傪 斾妑偡傞偲丄
丂丂丂(x+120*30)/(4*30)=(x+120*15)/(6*15)
丂丂丂x/120+30=x/90+20
丂丂丂10=x/360
丂丂丂x=3600
傛偭偰丄傕偲偺帺摦幵偺戜悢偼3600戜丅
夝摎丒偦偺13
乮儁儞僱亅儉丗DDT乯
枅暘120戜偺幵偑棃偰丄僎乕僩1売強偑枅暘y戜張棟偡傞偲偡傞偲丄 僎乕僩4売強偱幵楍偼枅暘 (4y亅120)戜 抁偔側傞丅30暘偱幵楍偼側偔側傞偐傜丄 嵟弶偺幵楍偺戜悢偼丄30亊(4y亅120) 戜丅
摨條偵丄僎乕僩6売強側傜丄15亊(6y亅120) 戜丅椉幰偼摍偟偄偐傜丄
丂丂丂30亊(4y亅120)亖15亊(6y亅120)
丂丂丂4y亅120亖3y亅60
丂丂丂y亖亅60亄120亖60 戜/暘
廬偭偰丄嵟弶偺幵楍偼丄
丂丂丂30亊(4y亅120)亖30亊(4亊60亅120)亖30亊120亖3600 戜
偲側傝傑偡丅 偪側傒偵偙偺寢壥偼丄幵偺棳擖戜悢偲僎乕僩張棟擻椡偑堦掕偲偟偰丄 僎乕僩傪4傑偨偼6売強偵偡傞埲慜偺奐曻僎乕僩悢丄偍傛傃幵楍偑棴傑偭偰偄偭偨帪娫偵偼柍娭學偱偡丅 壗屘側傜丄僎乕僩傪4傑偨偼6売強偵偟偨弖娫偺幵楍偺戜悢傪x偲偡傞偲丄
丂丂丂x亖(兛亅60倣)t
偱側偗傟偽側傝傑偣傫丅
傕偪傠傫t亖0偐傜x亖3600 戜偵側傞弖娫傑偱丄枅暘偺幵偺棳擖兛偼丄兛亜倣y亖60倣 戜/暘 偲壖掕偝傟傑偡丅偙偙偱 倣偼丄x亖3600 戜偵側傞埲慜偺奐曻僎乕僩悢偱偡丅 側傫偩偐岎捠岺妛偵偍偗傞丄摴楬偺崿傒嬶崌曽掱幃傪巚偄弌偟傑偡丅幵偺棳擖検偑丄 帪娫偵懳偟偰晄楢懕偵曄壔偡傞栤戣傪嶌傝偨偔側偭偰偒傑偟偨丅 偦傟偼丄2曄悢偺憃嬋宆曃旝暘曽掱幃傪摿惈嬋慄偺曽朄偱夝偔抜攇偺寁嶼偵側傝傑偡 乮仼 嶌傟傞偐偳偆偐傢偐傝傑偣傫乯丅
夝摎丒偦偺14
乮儁儞僱亅儉丗nao乯
乮摎埬乯
侾偮偺僎乕僩偱侾暘娫偵張棟偱偒傞戜悢傪乽侾乿偲偍偔偲丄
丂丂丂係売強奐偄偨応崌偼乽侾乿亊係亊俁侽亖乽侾俀侽乿
丂丂丂俇売強奐偄偨応崌偼乽侾乿亊俇亊侾俆亖乽俋侽乿
偙偺嵎偺乽俁侽乿偼俁侽暘偲侾俆暘偺嵎偱偁傞侾俆暘娫偵傗偭偰偒偨戜悢偺嵎偵摉傞丅
丂丂侾俀侽亊侾俆亖侾俉侽侽戜丂侾俉侽侽亐乽俁侽乿亖俇侽戜
侾偮偺僎乕僩偼侾暘娫偵俇侽戜張棟偱偒傞丅 侾暘娫偵傗偭偰偔傞戜悢偼侾俀侽戜側偺偱丄 侾俀侽亐俇侽亖俀偮偺僎乕僩偑偁傟偽張棟偱偒傞丅 係偮偺僎乕僩偱俁侽暘偱張棟偱偒偨偺偩偐傜丄係偮偺撪俀偮偺僎乕僩偼怴偟偔傗偭偰 偔傞幵偩偗傪張棟偡傞偲偟偰丄巆傝偺俀偮偑嵟弶偵偁偭偨楍傪張棟偟偨偙偲偵側傞丅
丂丂丂俇侽戜亊俀亊俁侽暘亖俁俇侽侽戜丒丒丒偙偨偊
夝摎丒偦偺15
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
弶傔偵偁偭偨楍偺帺摦幵傪乽仭乿偱昞偟傑偡丅
偦偺楍偺屻偵憹偊傞帺摦幵傪乽仩乿偱昞偟傑偡丅
椏嬥強偺僎乕僩傪乽仼乿偱昞偟傑偡丅
帺摦幵偺検傪峫偊傞偆偊偱丄 僎乕僩偐傜弌傞帺摦幵偑傕偲傕偲幵楍偵偁偭偨傕偺偐丄 屻偐傜憹偊偨傕偺偐傪嬫暿偡傞昁梫偑偁傝傑偣傫丅
僎乕僩傪係僇強奐偄偰幵楍偑30暘偱側偔側偭偨條巕傪昞偟傑偡丅
丂 丂 0丂丂丂丂丂 15丂丂丂丂丂丂丂30 丂丂嘆仼丂仭仭仭仭仭仭乥仭仭仭仭仭仭 丂丂嘇仼丂仭仭仭仭仭仭乥仭仭仭仭仭仭 丂丂嘊仼丂仩仩仩仩仩仩乥仩仩仩仩仩仩 丂丂嘋仼丂仩仩仩仩仩仩乥仩仩仩仩仩仩師偵僎乕僩傪俇僇強奐偄偰幵楍偑15暘偱側偔側偭偨條巕傪昞偟傑偡丅
丂 0丂丂丂丂丂 15丂丂丂丂丂丂丂30 丂丂嘆仼丂仭仭仭仭仭仭乥 丂丂嘇仼丂仭仭仭仭仭仭乥 丂丂嘊仼丂仩仩仩仩仩仩乥 丂丂嘋仼丂仩仩仩仩仩仩乥 丂丂嘍仼丂仭仭仭仭仭仭乥 丂丂嘐仼丂仭仭仭仭仭仭乥僎乕僩傪俇僇強偵偟偨偲偒嘍丒嘐偺僎乕僩偐傜弌偨帺摦幵偼丄
僎乕僩偑係僇強偺偲偒偵15暘偡偓偐傜30暘偺娫偵嘊丒嘋偺僎乕僩偐傜弌偨帺摦幵偲摨偠検偱偡丅
僎乕僩偑俇僇強偺偲偒15暘偱幵楍偑側偔側偭偨偲偄偆偙偲偼丄
嘍丒嘐偺僎乕僩偐傜弌偨帺摦幵偼丄
僎乕僩偑係僇強偺偲偒偵15暘偡偓偐傜30暘偺娫偵嘆丒嘇偺僎乕僩偐傜弌偨帺摦幵偲摨偠検偱偡丅
15暘偱憹偊傞帺摦幵偺検偼丄侾俀侽亊15亖侾俉侽侽戜偱偡丅
偩偐傜弶傔楍偵偁偭偨帺摦幵偼丄攞偺俁俇侽侽戜偱偡丅
惓夝幰
teki 偺偭偙傫 僆儎僕 僥儗僗偲傾儕僗 T_Tatekawa nao Toru 岼偺柌 俥倎倳倱俿 忨偺偍偠偝傫 栭傆偐偟偺偮傜偄偍偠偝傫 DDT 傂傠 namiusagi 嶰妏掕婯
堦掕偺妱崌偱尭偭偰偄偔堦曽偱丄暿側梫慺偵傛傝堦掕偺妱崌偱憹偊偰偄偔偲偄偆 忬嫷壓偵偁傞検傪峫偊傞栤戣傪僯儏乕僩儞嶼偲偄偄傑偡丅 偙偺栤戣偼丄崅懍摴楬偺椏嬥強偺僎乕僩偱張棟傪偟偰偄傞堦曽偱丄 暲傇帺摦幵偺戜悢偑憹偊偰偄偔偲偄偆偙偲偵側傝傑偡丅
楢棫曽掱幃傪棫偰偰夝偄偰偄偨偩偄偨曽偑懡偄傢偗偱偡偹丅 僥儗僗偲傾儕僗偝傫丄Toru偝傫偼丄係売強偩偲俁侽暘丄俇売強偩偲侾俆暘偲偄偆偲偙傠偐傜丄 斾傪梡偄偰夝偄偰偔偩偝偄傑偟偨丅 傑偨丄nao偝傫丄栭傆偐偟偺偮傜偄偍偠偝傫 偺夝摎傪攓尒偡傞偲丄曽掱幃傪巊傢側偔偰傕丄傓偟傠巊傢側偄曽偑丄 偟偭偔傝棟夝偱偒傑偡偹丅偳偆傕偁傝偑偲偆偛偞偄傑偟偨丅

 E-mail
E-mail
 top
top