侾侾係丏棫懱偺愗抐
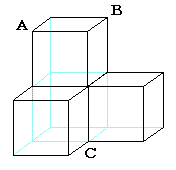
恾偺傛偆偵丄侾曈偺挿偝偑2cm偺棫曽懱傪係屄偼傝崌傢偣偰偱偒偨棫懱傪峫偊傑偡丅 偙偺棫懱傪俁偮偺捀揰俙丄俛丄俠傪捠傞暯柺偱愗抐偟傑偡丅
乮侾乯嶰妏宍俙俛俠偺柺愊傪媮傔側偝偄丅
乮俀乯愗傝岥偺恾宍偺柺愊傪傕偲傔側偝偄丅
Weekend Mathematics乛栤戣乛114偺栤戣
侾侾係丏棫懱偺愗抐

恾偺傛偆偵丄侾曈偺挿偝偑2cm偺棫曽懱傪係屄偼傝崌傢偣偰偱偒偨棫懱傪峫偊傑偡丅 偙偺棫懱傪俁偮偺捀揰俙丄俛丄俠傪捠傞暯柺偱愗抐偟傑偡丅
乮侾乯嶰妏宍俙俛俠偺柺愊傪媮傔側偝偄丅
乮俀乯愗傝岥偺恾宍偺柺愊傪傕偲傔側偝偄丅
戝恖偵栶棫偮嶼悢偺帪娫
庤搰彑楴丂娔廋
塱壀彂揦
夝摎丒偦偺1
乮儁儞僱亅儉丗僆儎僕乯
乮侾乯
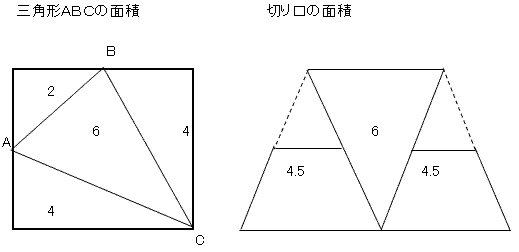
仮ABC偼丄嶰曈偑丄俀併俀丄俀併俆丄俀併俆偺擇摍曈嶰妏宍丄傛偭偰掙曈俀併俀丄崅偝俁併俀偺擇摍曈嶰妏宍
傛偭偰丄仮ABC亖乮侾乛俀乯亊俀併俀亊俁併俀亖俇噋俀乮俀乯
暯柺ABC偱愗抐偟偨棫曽懱偺侾偮偺暯柺偺堦偮偼丄併俀丄併俆丄併俆丄俀併俀偺摍媟戜宍
傛偭偰摍媟戜宍偼丄忋掙併俀丄壓掙俀併俀丄崅偝俁併俀乛俀偺摍媟戜宍
傛偭偰媮傔傞柺愊偼
仮ABC亄俀亊乮摍媟戜宍偺柺愊乯亖俇亄俀亊乮侾乛俀乯亊乮併俀亄俀併俀乯亊乮俁併俀乛俀乯亖俇亄俋亖侾俆噋俀
夝摎丒偦偺2
乮儁儞僱亅儉丗僥儗僗偲傾儕僗乯
乮侾乯亂夝摎亃
曈俙俛傪掙曈偲峫偊傞丅
掙曈偼丄(併俉)cm = (2併2)cm
崅偝偼丄(併(((2併2)/2)2+42))cm = (併18)cm = (3併2)cm
嶰妏宍俙俛俠偺柺愊 = ((2併2)亊(3併2)亊1/2)cm2 = 6cm2
丂丂丂摎偊丂6cm2
乮俀乯亂夝摎亃
媮傔傞柺愊偼丄俀偮偺戜宍偲嶰妏宍俙俛俠偺柺愊偺榓偲側傞丅
戜宍偺柺愊偼丄
忋曈偼丄((2併2)/2)cm
壓曈偼丄(併俉)cm = (2併2)cm
崅偝偼丄(併((((2併2)/2)/2)2+22))cm = (併(9/2))cm = (3/併2)cm
戜宍偺柺愊 = ((((2併2)/2)+(2併2))亊(3/併2))亊1/2 = 4.5cm2
傛偭偰丄愗傝岥偺恾宍偺柺愊 = 6cm2+(4.5cm2亊2) = 15cm2
丂丂丂摎偊丂15cm2
夝摎丒偦偺3
乮儁儞僱亅儉丗teki乯
侾丂俇們倣俀
俀丂侾俆們倣俀
侾丏 傑偲傕偵寁嶼偡傞偲寢峔戝曄偱偡偑丄壓偺恾偺偲偍傝丄侾曈係們倣偺惓曽宍偐傜捈妏嶰妏宍 俁偮傪愗傝庢傟偽丄嶼悢偱廫暘夝偗傑偡偹丅
俀丏 愗傝岥偺柺愊偼丄嶰妏宍俙俛俠傪俁偮暲傋偨傕偺偐傜丄嶰妏宍俙俛俠偺忋敿暘乮偙偺昞尰偼 旕忢偵晄惓妋偱偡偑丄梫偡傞偵柺愊偱尵偆偲係暘偺侾乯傪俀屄愗傝庢偭偨傕偺偵側傝傑偡丅 傛偭偰丄
丂丂丂俇亊乮俁亅侽丏俀俆亊俀乯亖俇亊俀丏俆亖侾俆們倣俀
偱偡偹丅
夝摎丒偦偺4
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊
乮侾乯嶰妏宍ABC偺柺愊偼丂丂俇cm2偱偡
乮俀乯愗傝岥偺恾宍偺柺愊偼丂侾俆cm2偱偡
侾丏
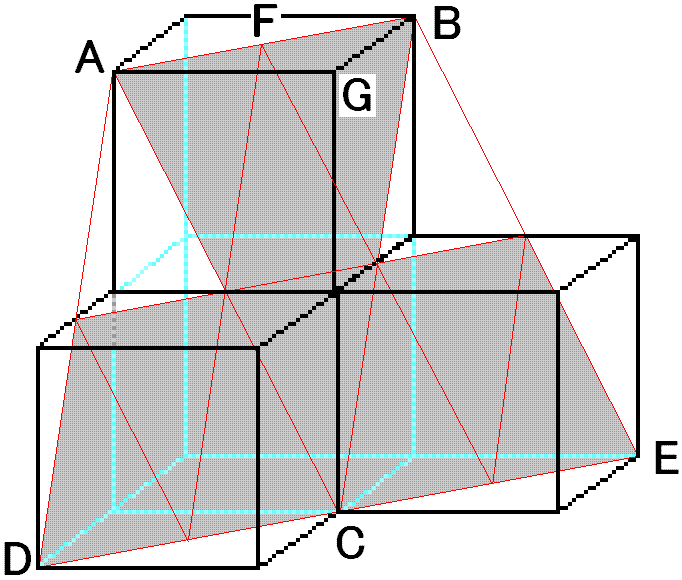
棫曽懱偺捀揰俙俛俠傪捠傞暯柺偺愗抐柺偺柺愊偼壓偺嶰妏悕揥奐恾傪尒偰壓偝偄丅 嶰妏悕揥奐恾傪揥奐偡傞偲係們倣巐曽偺惓曽宍偵側傞帠偑暘傝傑偡丅 愗抐柺俽偺柺愊傪師偺幃偱媮傔傑偡丅
丂丂丂俽亖惓曽宍偺柺愊乗乮俽侾亄俽俀亄俽俁乯
丂丂丂俽亖係亊係乗乮係亊俀乛俀乯亊俀亅俀亊俀乛俀亖俇cm2
俀丏
A偲B傪寢傇慄偐傜C偵岦偐偭偰愗抐偡傞偲壓偺慄偼D偲C偲E傪寢傇慄偵側傝傑偡丅 偦偟偰丄愗抐柺偼A丆B丆I丆俧丆俤丆俠丆俢丆俥偲側傝傑偡丅 偙偺柺愊偼侾偱媮傔偨仮ABC偺柺愊偺俁攞偐傜仮AFH偺柺愊偺俀攞暘傪堷偗偽媮傔傜傟傑偡丅 仮AFH偼仮ADC偵撪愙偡傞懠偺嶰妏宍偲偼崌摨偱偡丅 撪愙偡傞嶰妏宍偼仮AFH偲仮FDL偲仮FHL偲仮HIC偺係偮偱偡丅廬偭偰丄仮AFH偺柺愊偼
丂丂丂俇噋2乛係亖侾丏俆cm2
偱偡丅廬偭偰師偺幃偱愗抐柺傪媮傔傑偡丅
丂丂丂俇亊俁亅侾丏俆亊俀亖侾俆cm2
偱偡丅
嶰妏宍偑崌摨偱偁傞帠傪徹柧偡傞偨傔奺岎揰偵婰崋傪晅斣偟偰嶖妏丄摨埵妏偲愢柧偟傛偆偲巚偄傑偟偨偑丄愢柧偑挿偔側傝傑偡偺偱徣棯偄偨偟傑偡丅
夝摎丒偦偺5
乮儁儞僱亅儉丗岼偺柌乯
乮1乯
仮ABC偼AB傪掙曈偲偡傞擇摍曈嶰妏宍偲側傝丄 掙曈媦傃幬曈偺挿偝偼奺乆2併2偲2併5偱偡偺偱丄 媮傔傞柺愊S偼丄
丂丂丂S亖2併2亊3併2/2亖6
偲側傝傑偡丅
乮2乯
偪傚偭偲傗傗偙偟偄偺偱恾傪昤偒傑偡丅
慄暘AB偲暯峴偱C傪捠傞慄暘傪DE偲偟傑偡丅 偡傞偲媮傔傞愗傝岥偼愒偣傫偱埻傑傟偨恾宍 ABIGECDFHA偲側傝傑偡丅嶰暯曽偺掕棟 傛傝DE偼4併2丄AB偼俀併2丄HI偼併2 偱偁傞丅傑偨奺乆偺恾宍偺崅偝偼3併2偱 偁傞偐傜戜宍2偮値偍柺愊傪壛偊寁嶼 偡傞偲15偲側傞丅
夝摎丒偦偺6
乮儁儞僱亅儉丗嶰妏掕婯乯
丂抐柺偼丆塃恾偺悈怓偺晹暘偱偁傞丅
(1) 仮ABC 偼丆偺擇摍曈嶰妏宍偩偐傜丆崅偝偼
偱丆 柺愊偼 6 cm2
(2) 抐柺偺柺愊亖戜宍DEBA亊3亄仮CDE亖6亊(3/4)亊3亄6/4亖15 cm2
夝摎丒偦偺7
乮儁儞僱亅儉丗俥倎倳倱俿乯
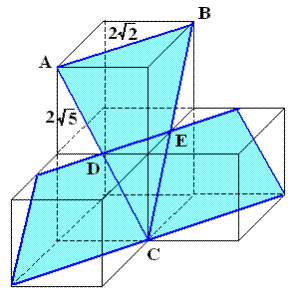
傑偢嵟弶偵丄俙俛俠偺懠偵丄曋媂忋彑庤偵婰崋傪晅偗偝偣偰捀偒傑偡丅 俠偐傜墧捈曽岦係們倣忋偵偁傞揰傪俢丄俙俛丄俙俠丄俛俠偺拞揰傪偦傟偧傟俫丄俵丄俶丄 偲偟傑偡丅
乮侾乯嶰妏宍俙俛俠偺柺愊
亂丂夝丂摎丂亃
嶰妏宍俙俛俠偺柺愊傪丂俽侾丂偲偡傞偲丄
丂丂丂俽侾亖(1/2)丒俙俛丒俠俫
俙俛亖俀併俀丄俠俫俀亖俠俢俀亄俢俫俀 俠俢亖係丄俢俫亖併俀丂傛傝丄
丂丂丂俠俫俀亖係俀亄乮併俀乯俀亖侾俇亄俀亖侾俉
俠俫亖併侾俉亖俁併俀乮俠俫亜侽傛傝乯
丂丂丂俽侾亖(1/2)丒俀併俀丒俁併俀亖俇
傛偭偰丄嶰妏宍俙俛俠偺柺愊偼丂俇們倣俀丂丂亂丂廔丂亃
乮俀乯愗傝岥偺恾宍偺柺愊
亂丂夝丂摎丂亃
乽愗傝岥乿偼係偮偺棫曽懱慡偰偵払偟偰偍傝丄偦偺偆偪丄侾偮偺棫曽懱乮愊傒廳側偭偰偄傞俀偮偺棫曽懱乮埲壓乽忋壓俀偮偺棫曽懱乿偲偡傞乯偺偆偪丄壓偺棫曽懱乯偺愗傝岥偑嶰妏宍偱丄偦偺懠偺俁偮偺棫曽懱乮忋壓俀偮偺棫曽懱偺偆偪丄忋偺棫曽懱偲丄忋壓俀偮偺棫曽懱埲奜偺俀偮偺棫曽懱乯偺愗傝岥偑俁偮偲傕崌摨側戜宍偵側偭偰偄傞丅 偙偺偙偲偑暘偐傟偽丄偁偲偼乮侾乯偺夝傪棙梡偡傟偽乮俀乯偺夝偼娙扨偵摫偗傞丅
乮侾乯偵傛傞嶰妏宍俙俛俠偺愗傝岥偼丄忋壓俀偮偺棫曽懱偵傢偨傞偑丄偙偺忋壓俀偮偺棫曽懱偺偦傟偧傟偺愗傝岥偵偮偄偰柺愊傪峫偊傞丅忋偺棫曽懱偺愗傝岥偼戜宍乮戜宍俙俵俶俛乯丄壓偺棫曽懱偺愗傝岥偼嶰妏宍乮仮俵俠俶乯偱偁傝丄偦傟偧傟偺柺愊傪丂俽俀丄俽俁丂偲偡傟偽丄師偺幃偑妋擣偱偒傞丅
丂丂丂戜宍俙俵俶俛丂丗丂俽俀
丂丂丂仮俵俠俶丂丂丗丂俽俁
丂丂丂俽俀亄俽俁亖俇丂乮乮侾乯偺亂夝亃乯丂丒丒丒嘆
偝偰丄俵丄俶偼俙俠丄俛俠偦傟偧傟偺拞揰偱偁傞偐傜丄嶰妏宍俙俛俠傪慄暘俵俶偵傛偭偰俀暘偝傟傞戜宍偲嶰妏宍偺柺愊俽俀丄俽俁偺娫偵偼師偺娭學幃偑惉傝棫偮丅
丂丂丂俽俀丗俽俁亖俁丗侾丂丒丒丒嘇
嘆丄嘇傛傝丄
丂丂丂俽俀亖俇亊俁乛係亖俋乛俀
丂丂丂俽俁亖俇亊侾乛係亖俁乛俀
媮傔傞愗傝岥丂俽丂偼丄戜宍乮俽俀乯偑俁偮偲丄嶰妏宍乮俽俁乯偑侾偮偺丄係偮偺恾宍偺崌寁偱偁傞偐傜丄
丂丂丂俽亖俽俀亊俁亄俽俁亖俋乛俀亊俁亄俁乛俀亖侾俆
傛偭偰丄媮傔傞愗傝岥偺恾宍偺柺愊偼丂侾俆們倣俀丂丂亂丂廔丂亃
夝摎丒偦偺8
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
乮侾乯仮ABC偵偍偄偰丄AB亖俀併俀丄俠俙亖俠俛亖俀併俆偱偡丅
偦偺侾
偡傞偲丄僿儘儞偺岞幃偐傜丄
仮俙俛俠 亖併乷乮俙俛亄俛俠亄俠俙乯乛俀丒乮亅俙俛亄俛俠亄俠俙乯乛俀丒乮俙俛亅俛俠亄俠俙乯乛俀丒乮俙俛亄俛俠亅俠俙乛俀乯乸 亖侾乛係丒併乷乮俀併俀亄俀併俆亄俀併俆乯乮亅俀併俀亄俀併俆亄俀併俆乯乮俀併俀亅俀併俆亄俀併俆乯乮俀併俀亄俀併俆亅俀併俆乯乸 亖侾乛係丒併乷乮係併俆亄俀併俀乯乮係併俆亅俀併俀乯丒俀併俀丒俀併俀乸 亖侾乛係丒併乷乮俉侽亅俉乯丒俉乸 亖俇
偦偺俀
梋尫掕棟傛傝丄俙俛2亖俠俛2亄俠俙2亅俀俠俛丒俠俙丒們倧倱俠
俉亖俀侽亄俀侽亅俀丒俀併俆丒俀併俆丒們倧倱俠 傛傝
丂丂丂們倧倱俠亖係乛俆丄倱倝値俠亖俁乛俆
丂亪仮俙俛俠亖侾乛俀丒俠俙丒俠俛丒倱倝値俠亖侾乛俀丒俀併俆丒俀併俆丒俁乛俆亖俇
偦偺俁
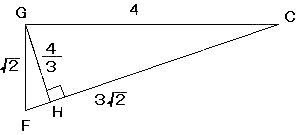
俙俛偺拞揰傪俥偲偟傑偡丅
丂 仮俠俥俧偵偍偄偰丄俧偐傜俠俥偵悅慄傪偍傠偟岎揰俫偲偟傑偡丅
偡傞偲丄俧俫亖係乛俁偱偡丅
嶰妏悕俠俙俛俧亖侾乛俁丒仮俙俛俠丒俧俫側偺偱丄
侾乛俁丒俀丒係亖侾乛俁丒仮俙俛俠丒係乛俁
丂亪仮俙俛俠亖俇
乮俀乯愗傝岥偺恾宍偼丄仮俙俛俠偺侾乛係偺戝偒偝偺嶰妏宍偑侾侽屄暘偁傝傑偡丅
偩偐傜丄侾侽丒侾乛係丒俇亖侾俆偱偡丅
夝摎丒偦偺9
乮儁儞僱亅儉丗Toru乯
掙柺偵搳塭偟偰峫偊傞偙偲偵偡傞偲
丂丂丂併(12+12)/併(12+12+42)=1/3
傛傝AB偲捈妏側曽岦偵偮偄偰丄侾乛俁偵弅傔偰偄傞偙偲偵側傞丅
侾乯 嶰妏宍俙俛俠偺搳塭偼堦曈俀cm偺惓曽宍偺敿暘偵側偭偰丄偙偺柺愊偼俀
傛偭偰傕偲偺柺愊偼俀x俁亖俇丂(cm2)
俀乯 抐柺偺搳塭偼堦曈俀cm偺惓曽宍偺敿暘偲丄 堦曈俀cm偺惓曽宍偺敿暘偐傜偦偺1/4偺朮巕傪偲偭偨傕偺偑擇偮偵側傞丅
丂丂丂2+3/2+3/2=5
傛偭偰傕偲偺柺愊偼5x3=15 (cm2)
惓夝幰
僆儎僕 teki Toru 岼偺柌 俥倎倳倱俿 僥儗僗偲傾儕僗 忨偺偍偠偝傫 嶰妏掕婯 栭傆偐偟偺偮傜偄偍偠偝傫
乮俀乯偺栤戣偱偼丄愗傝岥偺恾宍傪僀儊乕僕偱偒傑偟偨偱偟傚偆偐丅 柺愊傪媮傔傞偵偼丄偄傠偄傠側曽朄偑偁傞偲巚偄傑偡偑丄 傑偢偙偺愗傝岥偺宍忬傪惓妋偵攃埇偟側偄偲偄偗傑偣傫偹丅
傑偨丄柺愊傪媮傔傞曽朄偲偟偰丄Toru偝傫偺夝摎偼丄搳塭偟偨傕偺偺恾宍偺柺愊偐傜丄 尦偺柺愊傪媮傔傞偲偄偆傕偺偱丄戝曄儐僯乕僋偱嫽枴怺偄側偲巚偄傑偟偨丅

 E-mail
E-mail
 top
top