侾侾俁丏愊傒栘偺栤戣

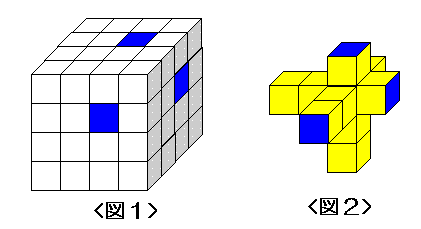
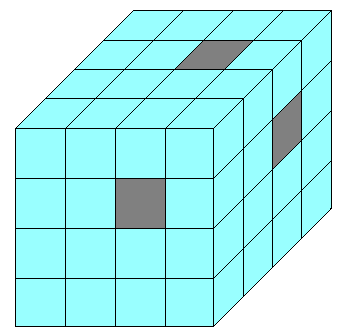
塃偺恾偼丄侾曈偑侾cm偺棫曽懱傪64屄崌傢偣偨棫曽懱偱偡丅 偙偺棫曽懱偺偐偘偺晹暘俁儢強偐傜丄偦傟偧傟斀懳懁傑偱暲傫偱偄傞棫曽懱傪偡傋偰 偔傝敳偄偰偱偒傞棫懱偑偁傝傑偡丅 偙偺棫懱偺懱愊偲昞柺愊傪媮傔側偝偄丅
Weekend Mathematics乛栤戣乛113偺栤戣
侾侾俁丏愊傒栘偺栤戣

塃偺恾偼丄侾曈偑侾cm偺棫曽懱傪64屄崌傢偣偨棫曽懱偱偡丅 偙偺棫曽懱偺偐偘偺晹暘俁儢強偐傜丄偦傟偧傟斀懳懁傑偱暲傫偱偄傞棫曽懱傪偡傋偰 偔傝敳偄偰偱偒傞棫懱偑偁傝傑偡丅 偙偺棫懱偺懱愊偲昞柺愊傪媮傔側偝偄丅
戝恖偵栶棫偮嶼悢偺帪娫
庤搰彑楴丂娔廋
塱壀彂揦
夝摎丒偦偺1
乮儁儞僱亅儉丗僆儎僕乯
侾曈侾噋偺俇係屄偺嬻摯傪暯峴堏摦偟偰堦嬿偵廤傔傞偲
懱愊丂俇係乕乮係亊俁乕俀乯亖俇係亅侾侽亖俆係噋俁
昞柺愊丗侾俆亊俇亄乮惵偄嬻摯偺昞柺愊乯丏丏丏嘆
乮惵偄嬻摯偺昞柺愊乯亖俁屄亊係噋俀亊俁捠傝亖俁俇噋俀丏丏丏嘇
嘆丄嘇傛傝丂丂昞柺愊亖俋侽亄俁俇亖侾俀俇噋俀
夝摎丒偦偺2
乮儁儞僱亅儉丗偡側偧偆乯
傑偢丄偔傝偸偔慜偺懱愊偲昞柺愊傪寁嶼偟偰偍偒傑偡丅
丂丂丂懱愊亖4亊4亊4亖64cm3
丂丂丂昞柺愊亖4亊4亊6亖96cm2
偔傝偸偐傟偨晹暘傪丄廳側偭偰偄傞晹暘傪峫偊偢偵敳偒弌偡偨傔偵暘夝偟偰峫偊偰傒傞丅 偮傑傝丄偔傝偸偐傟傞偺偼師偺傛偆側朹偺慻傒崌傢偣偱
丂丂丂a)丂仭仭仭仭
丂丂丂b)丂仭亊俀屄
丂丂丂c)丂仭仭亊俀屄
偺崌寁侾侽屄偺仭偑偔傝偸偐傟傞丅
偙偺仭堦屄偺懱愊偼1cm3偱偁傞偐傜丄偔傝偸偐傟偨懱愊偼10cm3丅
傛偭偰懱愊偼64乗10亖54cm3丒丒丒摎偊侾
師偵昞柺愊偩偑丄偔傝偸偐傟傞偲昞柺偺係屄偼側偔側傝丄撪懁偺晹暘偑憹偊傞丅
偦偺憹偊曽偼丄忋偺仭侾屄偵偮偄偰4cm2憹偊傞偙偲偵側傞偺偱丄昞柺愊偼
96乗4亄乮10亊係乯亖126cm2丒丒丒摎偊俀
夝摎丒偦偺3
乮儁儞僱亅儉丗teki乯
侾丂懱愊丂丂丂丂俆係們倣3
俀丂昞柺愊丂丂侾俀俇們倣2
偁傞掱搙偺嬻娫攃埇擻椡偑偁傟偽偱偒傑偡偹丅
懱愊偼丄俇係亅侾侽偱俆係丅乮偙傟偼丄恀傫拞偺棫曽懱偺廳暋偝偊尒棊偲偝側偗傟偽娙扨偱偡丅乯
栤戣偼昞柺愊偺曽偱偡偑丄俋俇亄俁俇亅俇偱侾俀俇偱偡丅
乮俁俇偺堄枴偼係亊俋偱偡偑丄亅俇偺堄枴偝偊傢偐傟偽丄偦傫側偵擄偟偔偼側偄偱偡偹丅乯
堦墳丄摢偺拞偱夝偒傑偟偨偑丄嬻娫攃埇擻椡偺朢偟偄巹偺偙偲偱偡偺偱丄娫堘偊偰傞偐傕(^^;;
夝摎丒偦偺4
乮儁儞僱亅儉丗Toru乯
偔傝敳偐傟傞棫曽懱偺悢偼侾侽屄偱丄懱愊偼54 cm3
奜柺偺柺愊偑15x6=90 cm2 僩儞僱儖偺暻偺柺愊偑4x3x3=36 cm2偱丂昞柺愊 偼90+36=126 cm2
夝摎丒偦偺5
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊
棫曽懱偺懱愊偼丂俆係們倣3丂偱偡
棫曽懱偺昞柺偺柺愊偼丂侾俀俇們倣2丂偱偡
棫曽懱偺懱愊偵偮偄偰
慡懱偺懱愊
丂丂丂係亊係亊係亖俇係cm3
敳偒庢傞懱愊
丂丂丂乮俁屄暲傫偩棫曽懱傪俁売強暘偺懱愊乯亄乮拞怱偺棫曽懱侾屄偺懱愊乯亖敳偒庢傞懱愊
丂丂丂乮侾亊侾亊俁亊俁乯亄乮侾亊侾亊侾乯亖侾侽們倣3
廬偭偰丂丂俇係亅侾侽亖俆係們倣3
棫曽懱偺昞柺偺柺愊偵偮偄偰
慡懱偺塭偱側偄晹暘偺昞柺偺柺愊
丂丂丂係亊係亊俇亅俇亖俋侽們倣2
敳偒庢偭偨強偺昞柺偺柺愊
丂丂丂侾亊侾亊俁亊係亊俁亖俁俇們倣2
廬偭偰丂丂俋侽亄俁俇亖侾俀俇們倣2
夝摎丒偦偺6
乮儁儞僱亅儉丗偺偭偙傫乯
嘆懱愊
丂侾乯x曽岦偵偔傝敳偔仺係屄尭傞
丂俀乯師偵y曽岦偵偔傝敳偔仺俁屄尭傞
丂俁乯偝傜偵z曽岦偵偔傝敳偔仺俁屄尭傞
丂寢嬊侾侽屄尭傞偐傜丄俇係亅侾侽亖俆係乮棫曽僙儞僠儊乕僩儖乯
嘇昞柺愊
丂侾乯x曽岦偵偔傝敳偔
丂丂丂仺係亊係亅俀亖侾係乮暯曽僙儞僠儊乕僩儖乯憹偊傞
丂俀乯師偵y曽岦偵偔傝敳偔
丂丂丂仺係亊俁亅係亖俉乮暯曽僙儞僠儊乕僩儖乯憹偊傞
丂俁乯偝傜偵z曽岦偵偔傝敳偔
丂丂丂仺係亊俁亅係亖俉乮暯曽僙儞僠儊乕僩儖乯憹偊傞
丂寢嬊丄俁侽暯曽僙儞僠儊乕僩儖憹偊傞偐傜
丂丂丂侾俇亊俇亄俁侽亖侾俀俇乮暯曽僙儞僠儊乕僩儖乯
夝摎丒偦偺7
乮儁儞僱亅儉丗T_Tatekawa乯
嵗昗傪巊偭偨曽偑愢柧偟傗偡偄偺偱丆嵗昗傪摫擖偟傑偡丏 嵍偐傜塃偵 x 幉丆庤慜偐傜墱偵 y 幉丆壓偐傜忋偵 z 幉傪庢傝丆 奺乆偺棫曽懱偺埵抲傪丆椺偊偽惓柺偺偐偘偺晹暘偺棫曽懱側傜偽 (3, 1, 3) 偲偄偆傛偆偵昞偡帠偵偟傑偡丏
(3, 1, 3) 偲 (4, 3, 3) 偺棫曽懱偺偲偙傠傪慡偰偔傝偸偄偨応崌丆 僩儞僱儖偺岎嵎偡傞応強偼 (3, 3, 3) 偵側傞丏 傑偨丆(3, 3, 4) 偲 (3, 1, 3) 偐傜偔傝偸偄偨応崌偺 僩儞僱儖偺岎嵎偡傞応強傕 (3, 3, 3) 偵側傞丏 傛偭偰嶰偮偺僩儞僱儖偼 (3, 3, 3) 偱岎嵎偡傞帠偵側傞偺偱丆 敳偄偨棫曽懱偺悢偼
丂丂丂(4-1) * 3 + 1 = 10 屄
懱愊偼
丂丂丂64-10 = 54 cm3
昞柺愊偵娭偟偰偼丆傑偢僩儞僱儖傪偔傝偸偔帠偵傛傝丆彫棫曽懱偺 榋柺暘傪幐偆丏 堦曽偱丆僩儞僱儖偺撪暻偺昞柺愊偼丆彫棫曽懱堦屄偁偨傝偱 4cm2 偵側傞丏 僩儞僱儖偺岎嵎偟偰偄傞晹暘傪彍偄偰丆僩儞僱儖偺撪暻偺昞柺愊偩偗丆 棫懱偺昞柺愊偑憹偊傞偺偱丆棫懱偺昞柺愊偼
丂丂丂4*4 * 6 - 6 + 4*9 = 126 cm2
夝摎丒偦偺8
乮儁儞僱亅儉丗岼偺柌乯
崱夞偺栤戣偱偡偑丄尦偺棫懱偺懱愊偲柺愊傪嶼掕偟偰偍偒偐偘偺晹暘傪嵎偟堷偔偲偄偆僆乕僜 僪僢僋僗側庤朄偱峫偊傑偟偨丅拲堄偡傞偺偼3偮偑廳側傞売強偱偡偹丅
V亖43亖64噋3丂丂丂S亖42亊6亖96噋2
偙傟傜偐傜丂10噋3傪堷偒丄12亊3-6亖30噋2傪壛偊傟偽傛偄偺偱丄 媮傔傞傕偺偼54噋3偲126噋2偲側傞丅
夝摎丒偦偺9
乮儁儞僱亅儉丗俥倎倳倱俿乯
亂夝丂摎亃
懱丂愊丗丂丂俆係丂棫朄僙儞僠儊乕僩儖
昞柺愊丗丂侾俀俇丂暯曽僙儞僠儊乕僩儖
懱愊丗
侾売強偐傜斀懳懁傑偱偔傝敳偔棫曽懱偺悢偼係屄乮偙傟傪乽偔傝敳偄偨係屄乿偲偟傑偡乯丅
偦傟偑俁偮偁傝傑偡偑丄乽偔傝敳偄偨係屄乿偼俁偮偲傕摨偠応強偱岎嵎偟偰傑偡偺偱丄
丂丂丂係亄乮係亅侾乯亄乮係亅侾乯亖侾侽乮屄乯
偑丄戣堄傪枮偨偡丄偔傝敳偄偨晹暘偺屄悢偵側傝傑偡丅
偔傝敳偔慜偺慡懱偺屄悢偑俇係屄丄偔傝敳偄偨屄悢偑侾侽屄偱丄巆傝偼俆係屄丅
傛偭偰丄媮傔傞懱愊偼
丂丂丂俆係丂棫朄僙儞僠儊乕僩儖丂
偱偡丅
昞柺愊丗
偔傝敳偔慜偺俇係屄偺棫曽懱偺昞柺愊乮扨埵徣棯丒埲壓摨偠乯偼丄
丂丂丂係亊係亊俇亖俋俇丒丒丒嘆
偙偺偆偪丄偔傝敳偄偨偙偲偵傛傝徚幐偟偨晹暘偑俇売強偁傞偺偱丄偦偺柺愊偼丄
丂丂丂俇丒丒丒嘇
師偵丄偔傝敳偄偨晹暘偵弌棃偨丄俇係屄偺棫曽懱偺乽撪晹乿偺柺愊傪峫偊傑偡丅
偔傝敳偄偨棫曽懱偺屄悢偼侾侽屄丅
偙偺侾侽屄偺偆偪丄侾屄偼俇係屄偺棫曽懱偺撪晹偲侾柺傕愙偟偰偍傜偢 乮俇柺偲傕偔傝敳偄偨棫曽懱偵愙偟偰偄傞乯丄 巆傞偡傋偰偺俋屄偼丄係柺偑俇係屄偺棫曽懱偺撪晹偵愙偟偰偄傞 乮巆傞俀柺偼偔傝敳偄偨棫曽懱偵愙偟偰偄傞偐丄嘇偵傛傞晹暘乯偺偱丄 偙偺晹暘偺柺愊偼丄
丂丂丂係亊俋亖俁俇丒丒丒嘊
嘆亅嘇亄嘊傛傝
丂丂丂俋俇亅俇亄俁俇亖侾俀俇
傛偭偰丄媮傔傞昞柺愊偼丄
丂丂丂侾俀俇丂暯曽僙儞僠儊乕僩儖
偱偡丅丂丂乮埲丂忋乯
夝摎丒偦偺10
乮儁儞僱亅儉丗抴鍋偺憙忛乯
僨僢僒儞傪偟偰偟傑偄傑偟傚偆丅

僽儘僢僋偼10屄丅6柺偺偆偪5柺傪奜婥偵偝傜偟偰偄傞僽儘僢僋偑6屄丅 4柺偼3屄丅慡偔奜婥偵怗傟側偄僽儘僢僋偑1屄丅 偩偐傜丄42柺偑昞柺愊傪嶌偭偰偄傑偡丅 偟偨偑偭偰丄懱愊10們倣3丂丂昞柺愊42們倣2
乽偔傝偸偔乿偲暡乆偵側傞偩傠偆偐傜丄傕偟偐偟偨傜巆傞寠偺奐偄偨棫懱偺偙偲偱偟傚偆偐丅 偦偟偨傜丄54們倣3偲126們倣2
夝摎丒偦偺11
乮儁儞僱亅儉丗嶰妏掕婯乯
[懱愊] <恾侾>偺棫曽懱偐傜<恾俀>傪彍偄偰 64亅10亖54 cm3
[昞柺愊] <恾侾>偺棫曽懱偺昞柺愊偐傜<恾俀>偺惵怓傪彍偒墿怓傪壛偊乮 棤懁偺尒偊側偄晹暘傕娷傔偰乯傟偽傛偄丅
丂丂丂16亊6亅6亄4亊9亖126 cm2
夝摎丒偦偺12
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
偙偺棫曽懱偺奃怓偺晹暘俁儢強偐傜丄偦傟偧傟斀懳懁傑偱暲傫偱偄傞棫曽懱傪偡傋偰偔傝敳偔偲 巼怓偺晹暘偑壓偵偢傟傑偡丅
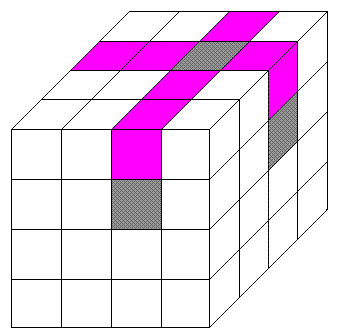

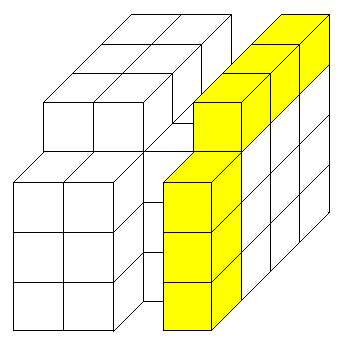
偦偟偰墿椢怓偺晹暘傪墱偵偢傜偟丄嵟屻偵墿怓偺晹暘傪嵍偵偢傜偟傑偡丅
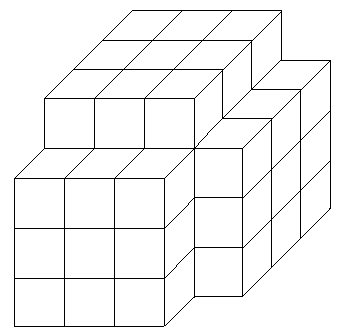
嵟屻偺恾偱尒偊側偄晹暘偵偼丄3亊3亊3=27屄偺棫曽懱偑偁傝丄尒偊傞偲偙傠偵傕3亊3亊3=27屄偺棫曽懱偑偁傝傑偡丅 偩偐傜丄寁54屄偺棫曽懱偑偁傞偺偱丄懱愊偼54棫曽僙儞僠儊乕僩儖偱偡丅
師偵尦偺恾偱忋偺柺偺棫懱傪嵍傊90搙夞偟傑偡丅 偦偺屻塃懁偺柺傪塃傊90搙夞偟傑偡丅
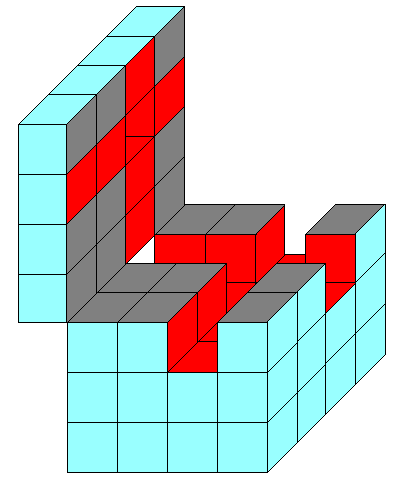
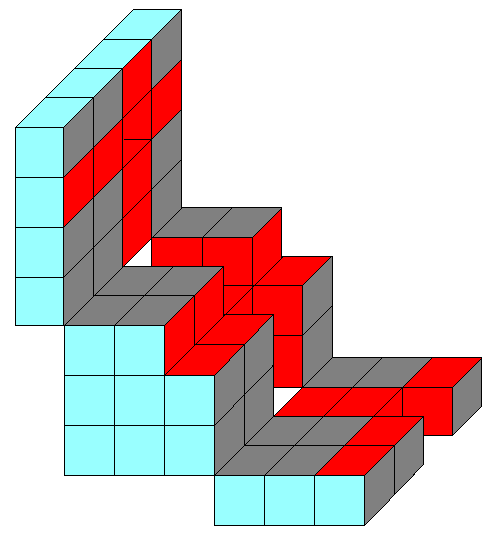
塃偺恾偱悈怓偺晹暘偼丄棫懱傪偔傝敳偔慜偵昞柺偱偁偭偨偲偙傠偱偡丅 愒偄晹暘偼棫懱傪偔傝敳偄偨偨傔偵丄怴偨偵昞柺偵側偭偨晹暘偱偡丅 惓曽宍偼丄悈怓偑6亊乮4亊4-1乯=90屄丄愒偑3亊乮3亊4乯=36屄偱寁126屄偁傝傑偡丅 偩偐傜丄昞柺愊偼丄126暯曽僙儞僠儊乕僩儖偱偡丅
惓夝幰
teki 岼偺柌 忨偺偍偠偝傫 偺偭偙傫 T_Tatekawa 栭傆偐偟偺偮傜偄偍偠偝傫 Toru 偡側偧偆 僆儎僕 俥倎倳倱俿 抴鍋偺憙忛 嶰妏掕婯
廳暋偟偰偄傞晹暘傪娫堘偄側偔悢偊偰偄偗偽夝寛偟傑偡偹丅 昞柺愊傪媮傔傞偨傔偵丄棫懱傪揥奐偟偰偟傑偆偲偄偆栭傆偐偟偺偮傜偄偍偠偝傫 偺夝摎偼側偐側偐儐僯乕僋偱偡偹丅

 E-mail
E-mail
 top
top