112.円すいに巻いた糸の長さ
下の図のような円すいがあります。この底面の周上の点Aから円すいにひもを2回り巻きつけてAに戻るとき、ひもの長さが最短になる場合は何cmでしょうか。
Weekend Mathematics/問題/112の問題
112.円すいに巻いた糸の長さ
下の図のような円すいがあります。この底面の周上の点Aから円すいにひもを2回り巻きつけてAに戻るとき、ひもの長さが最短になる場合は何cmでしょうか。
大人に役立つ算数の時間
手島勝朗 監修
永岡書店
解答・その1
(ペンネ-ム:浜田 明巳)
この円すいの頂点をOとし,OAに沿って側面を切り取る展開図を考える.底面の半径が2,母線の長さが24であるから,展開図のおうぎ形の中心角は,
360°×2/24=30°(プログラムではk)
ひもを2周するのであるから,このおうぎ形を2つつないだ中心角60°のおうぎ形を考えればよい. 図からOA1=OA3,∠A1OA3=60°となるので,△OA1A3は正三角形となる. 故に求める長さは,A1A3間の最短距離である
A1A3=OA1=24(cm)
となる.
Visual Basicでのプログラムを作ってみた.このプログラムにより,ひもの巻き具合がよく分かる.
Option Explicit Sub Form_Load() Picture1.BackColor = vbWhite Picture1.Scale (-11, 20)-(11, -2) Picture2.BackColor = vbWhite Picture3.BackColor = vbWhite Picture3.Picture = LoadPicture("mondai112a.gif") Picture4.BackColor = vbWhite Picture4.Scale (-13, 1)-(14, -26) End Sub Sub Command1_Click() Dim O1x As Double '円すいの頂点 Dim O1y As Double Dim O1z As Double Dim A1x As Double Dim A1y As Double Dim A1z As Double Dim P1x As Double '円すいの底面の円周上の点 Dim P1y As Double Dim P1z As Double Dim Q1x As Double '糸上の点 Dim Q1y As Double Dim Q1z As Double Dim O2x As Double '展開図の頂点(おうぎ形の中心) Dim O2y As Double Dim A21x As Double Dim A21y As Double Dim A22x As Double Dim A22y As Double Dim A23x As Double Dim A23y As Double Dim P2x As Double '展開図のおうぎ形の弧上の点 Dim P2y As Double Dim Q2x As Double '展開図の糸上の点 Dim Q2y As Double Dim x1_min As Double Dim y1_min As Double Dim x1_max As Double Dim y1_max As Double Dim xx As Double Dim yy As Double Dim OQ As Double Dim k As Double '展開図のおうぎ形の中心角 Dim t As Double Dim kizami As Double Dim tenhankei As Double ' O1x = 0 O1y = 0 O1z = Sqr(24 * 24 + 2 * 2) O2x = 0 O2y = 0 A1x = 0 A1y = 2 A1z = 0 P1z = 0 k = 2 / 24 * 360 A21x = 24 * Cos(radian(270 - k)) A21y = 24 * Sin(radian(270 - k)) A22x = 0 A22y = -24 A23x = -A21x A23y = A21y Q2y = A21y kizami = 0.1 x1_min = 2 x1_max = -2 tenhankei = 0.1 Picture1.Cls For t = 0 To 360 Step kizami xx = f3(2 * Cos(radian(t)), 2 * Sin(radian(t)), 0, 1) yy = f3(2 * Cos(radian(t)), 2 * Sin(radian(t)), 0, 2) Picture1.PSet (xx, yy), vbBlack If x1_min > xx Then x1_min = xx y1_min = yy End If If x1_max < xx Then x1_max = xx y1_max = yy End If Next t Picture1.Line (x1_min, y1_min)-(f3(O1x, O1y, O1z, 1), f3(O1x, O1y, O1z, 2)), vbBlack Picture1.Line -(x1_max, y1_max), vbBlack Picture1.Line -(f3(0, 0, 0, 1), f3(0, 0, 0, 2)), vbBlack Picture1.Circle (f3(2, 0, 0, 1), f3(2, 0, 0, 2)), tenhankei, vbRed '点A Picture1.CurrentX = f3(2, 0, 0, 1) Picture1.CurrentY = f3(2, 0, 0, 2) Picture1.Print "A" Picture1.CurrentX = f3(O1x, O1y, O1z, 1) Picture1.CurrentY = f3(O1x, O1y, O1z, 2) Picture1.Print "O" Picture4.Cls Picture4.Line (A21x, A21y)-(O2x, O2y), vbBlack Picture4.Line -(A23x, A23y), vbBlack Picture4.Line (O2x, O2y)-(A22x, A22y), vbBlack Picture4.Circle (O2x, O2y), 24, vbBlack, radian(270 - k), radian(270 + k) Picture4.Circle (A21x, A21y), tenhankei, vbRed Picture4.Circle (A22x, A22y), tenhankei, vbRed Picture4.Circle (A23x, A23y), tenhankei, vbRed Picture4.CurrentX = A21x Picture4.CurrentY = A21y Picture4.Print "A1" Picture4.CurrentX = A22x Picture4.CurrentY = A22y Picture4.Print "A2" Picture4.CurrentX = A23x Picture4.CurrentY = A23y Picture4.Print "A3" Picture4.CurrentX = O2x Picture4.CurrentY = O2y Picture4.Print "O" kizami = 0.0005 For t = 270 - k To 270 + k Step kizami P2x = 24 * Cos(radian(t)) P2y = 24 * Sin(radian(t)) Q2x = (P2x - O2x) / (P2y - O2y) * (Q2y - O2y) + O2x OQ = Sqr((Q2x - O2x) * (Q2x - O2x) + (Q2y - O2y) * (Q2y - O2y)) P1x = 2 * Cos(radian((t - (270 - k)) * 360 / k)) P1y = 2 * Sin(radian((t - (270 - k)) * 360 / k)) Q1x = ((24 - OQ) * O1x + OQ * P1x) / (OQ + (24 - OQ)) Q1y = ((24 - OQ) * O1y + OQ * P1y) / (OQ + (24 - OQ)) Q1z = ((24 - OQ) * O1z + OQ * P1z) / (OQ + (24 - OQ)) Picture1.PSet (f3(Q1x, Q1y, Q1z, 1), f3(Q1x, Q1y, Q1z, 2)), vbRed Picture4.PSet (Q2x, Q2y), vbRed Picture2.Cls Picture2.Print Sqr((Q2x - A21x) * (Q2x - A21x) + (Q2y - A21y) * (Q2y - A21y)); "cm" Next t End Sub Sub Command2_Click() Unload Me End Sub Private Function f3(ByVal x As Double, ByVal y As Double, ByVal z As Double, ByVal i As Integer) As Double '空間座標を平面座標に変換 Dim x1 As Double Dim y1 As Double Dim z1 As Double Dim x2 As Double Dim y2 As Double Dim Px As Double Dim Py As Double x1 = y * Cos(rotate(2)) + x * Sin(rotate(2)) 'z軸回り y1 = z z1 = -y * Sin(rotate(2)) + x * Cos(rotate(2)) x2 = x1 'y軸回り y2 = y1 * Cos(rotate(1)) - z1 * Sin(rotate(1)) Px = x2 * Cos(rotate(3)) - y2 * Sin(rotate(3)) 'z軸回り Py = x2 * Sin(rotate(3)) + y2 * Cos(rotate(3)) If i = 1 Then f3 = Px Else f3 = Py End If End Function Private Function rotate(ByVal i As Integer) As Double Select Case i Case 1 'y軸について回転 rotate = radian(35) Case 2 'z軸について回転 rotate = radian(-60) Case Else 'x軸について回転 rotate = 0 End Select End Function Private Function radian(ByVal x As Double) As Double radian = 4 * Atn(1) / 180 * x End Function
解答・その2
(ペンネ-ム:teki)
答え 24cm
円錐の展開図を描くと、側面は半径24cm、中心角30度の扇形になります。 ひもを2周巻きつけるのですから、その最短経路は、半径24cm、中心角60度 の扇形上で直線(この扇形の弦)になります。 よって、その長さはできる三角形が正三角形なので、扇形の半径と同じ24cm ですね。 図を描いてみれば一発ですが、あえて頭の中だけで解きました。
ところで、昨今の小中学校では、円周率πを3として計算させている ところが多くあると聞いています。 そうすると、底面の円周はちょうど12cmになっちゃいます。 ということは、この問題の場合、底面に沿ってひもを2回巻きつければ これが正解と同じ値になってしまいます。 これだと、せっかくのいい問題が台無しですね。 何事も省略しちゃいけません。
ある国では、円周率πを3.16と法律で決めているらしいです。 なぜ、3.16という値かというと、√10に近いからだそうです。 こちらのほうは、例えばオイラーのζ関数の値が非常にきれいになりますね。 例えば、ζ(2)=π2/6が5/3、ζ(4)=π4/90が10/9 等。 ことらのほうがお奨めですね。
解答・その3
(ペンネ-ム:杖のおじさん)
答え 24cmです
円すいを展開するとおうぎ形が出来ます。おうぎ形の頂角は次の計算で求めます。
糸を2巻きしますので次の図のようになります。
一周目の円すいの展開図はTAB、二周目の円すいの展開図はBTCです。
A点とC点をむ結んだ線の長さになります。
円すいの頂角の求め方
頂角=360°×(円すいの底面の半径)/(おうぎ形の半径)=360°×2/24=30°
2周するので三角形頂点∠ATB=30°×2=60°
TA=TC=24cmなので正三角形です。従って線分AC=24cmです。
解答・その4
(ペンネ-ム:のっこん)
この円すいの側面の展開図は半径24cmの十二分円。 2回りするから半径24cmの六分円を書き、 AとAを直線で結ぶと一辺の長さが24cmの正三角形となる。
(答)24cm
※「この問題は底面の半径を1とした時、母線の長さを4より大きくしないと成り立たない」 と思いますが、どうですか?
解答・その5
(ペンネ-ム:T_Tatekawa)
円すいの展開図を作ると,半径2cmの円と半径24cmの扇形の 組み合わせになる.演習の長さと弧の長さが同じなので,扇形の角度は
360 * (2/24) = 30 度
円すいの底面の周上の点からひもを2回り巻き付けてもとに戻るという事は, 扇形を二つつなげて,弧の両端を結ぶということ. この時の最短距離は弦になる.
扇形二つを合わせた角度は 60 度なので, 弦は扇形の半径二つと合わせて正三角形をなす. よって,最短距離は扇形の半径と同じ 24cm となり, 円すいにひもを2回り巻き付けて元に戻る最短距離は 24cm.
解答・その6
(ペンネ-ム:巷の夢)
円錐を展開すると頂角が30°の扇形になります。AからOAまでの最短経路は直線ですから12㎝となります。一周したあともう一周しながら元のAに戻らねばなりませんので、最短経路は今来た直線路となります。即ち元来た道と同様に戻れば良いので24㎝が解答です。
解答・その7
(ペンネ-ム:夜ふかしのつらいおじさん)
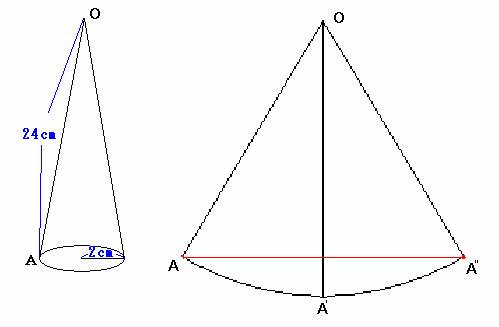
この円すいの展開図は、扇形OAA’です。
底面の円の半径をr、母線の長さをRとすると、
∠AOA’=360°×r/R=30°です。
糸を2回巻き付けるので、この展開図をもう1つ書いておきます。
この図でA、A’、A''は円すいを作ったときに重なります。
面に伸び縮みがない(曲がるだけ)ので、AとA''を結んだ長さが最短です。
△OAA''が正三角形になるので答えは24cmです。
解答・その8
(ペンネ-ム:yokodon)
円錐面の展開図を考えると良い。半径 24 cm の扇形になる方の、その中心角は
360°× 2/24 = 30°
である。
求めるひもの長さの最小値は、半径 24 cm の扇形の弧の両端点の各々から、それ と向かい合う線分(円錐の母線)に下ろした垂線の長さ2本の和に等しい。
円錐の頂点をO、この両端の点をA,Bとし、Aから線分OB、Bから線分OAに 下ろした垂線の足をP、Qとすると、∠OAP=∠OBQ= 60°なので、線分AP 、線分BQの長さは 12 cm
よって、求める長さは 24 cm となる。
解答・その9
(ペンネ-ム:Toru)
底面の周は4πであるから 円錐をAをとおる母線で切って展開すると 半径24 中心角π/6の扇形となる。2周まわすのだからこれを2つくっつけて、 中心角π/3 この扇形の底角から底角への最短距離を求めればよいが、これは直線 で中心角π/3から頂点もつなげば正三角形になるので 24cm--- 答え
解答・その10
(ペンネ-ム:三角定規)
与えられた円錐の展開図は下の <図1>のとおりで,側面を展開すると,中心角30゚の扇形OAA'となる。
<図2>のように,この扇形を2つ用意すると,円錐の側面に2回貼りつけることができ,このとき図の赤い線分AA'' は,円錐に2回巻きついてA に戻る,あきらかに最短の閉曲線である。 △OAA'' は正三角形だから,AA''=24 cm
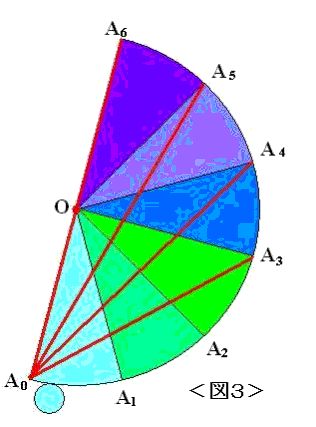
蛇足ながら,<図3> の A0A3,…,A0A6は, 円錐に3回,…6回糸を巻きつけるときの最短の糸の長さで,
となります。
最後のA0A6 は,円錐の頂点近くに6回巻きつけるもので,48+δ とすべきでしょうか。
正解者
のっこん teki 巷の夢 杖のおじさん Toru 浜田 明巳 yokodon T_Tatekawa 夜ふかしのつらいおじさん 三角定規
「ひもを2まわり」というところが、「扇形2個分」になるところがおもしろいですね。
のっこんさんのご質問「『この問題は底面の半径を1とした時、母線の長さを4より大きくしないと成り立たない』と思いますが、どうですか?」ですが、 この場合は、連結の扇形の中心角が180°を越えてしまいますから、同じ発想ではだめですね。 ただしその場合でも、2周する最短のコースというのは存在するはずですよね。
また、三角定規さんは、巻きつける回数を増やすとどうなるかという考察をしてくださいました。どうもありがとうございました。

 E-mail
E-mail
 top
top