侾侾侾丏儎僊偺栤戣
恾偺傛偆側彫壆偺偡傒偵儎僊偑俈倣偺傂傕偱偮側偑傟偰偄傑偡丅彫壆偺傑傢傝偵偼丄 堦柺偵憪偑偼偊偰偄傑偡丅儎僊偑怘傋傞偙偲偺偱偒傞憪抧偺柺愊傪媮傔側偝偄丅 偨偩偟丄儎僊偺戝偒偝偼峫偊側偄傕偺偲偟傑偡丅
Weekend Mathematics乛栤戣乛111偺栤戣
侾侾侾丏儎僊偺栤戣
恾偺傛偆側彫壆偺偡傒偵儎僊偑俈倣偺傂傕偱偮側偑傟偰偄傑偡丅彫壆偺傑傢傝偵偼丄 堦柺偵憪偑偼偊偰偄傑偡丅儎僊偑怘傋傞偙偲偺偱偒傞憪抧偺柺愊傪媮傔側偝偄丅 偨偩偟丄儎僊偺戝偒偝偼峫偊側偄傕偺偲偟傑偡丅
戝恖偵栶棫偮嶼悢偺帪娫
庤搰彑楴丂娔廋
塱壀彂揦
夝摎丒偦偺1
乮儁儞僱亅儉丗傒偄偨乯
傂傕偑俈儊乕僩儖側偺偱儎僊偼墌傪昤偄偰堏摦偡傞偲峫偊傑偟偨丅
丂丂丂侾亊侾亊俁丏侾係亐係
丂丂丂俈亊俈亊俁丏侾係亐係
丂丂丂俆亊俆亊俁丏侾係亐係
丂丂丂俁亊俁亊俁丏侾係亐係
偡傋偰偺柺愊傪懌偟偰丂摎偊偼丂俇俆丏俋俆倣2
夝摎丒偦偺2
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂俇俆丏俋俆暯曽儊乕僩儖
儎僊彫壆偺恾偺愢柧
CP=7m丂DQ=俆m丂ER=俁m丂CB=俇m丂PB=俈亅俇亖侾m亖AB
DQ=俈亅俀亖俆m亖DR丂丂ER=俆亅俀亖俁m亖EF
儎僊偑怘傋傞偙偲偺偱偒傞憪抧偺柺愊偼S1丄S2丄S3丄S4偺柺愊偺崌寁偱偡丅
S1偼B傪拞怱揰偲偟偰侾m偺墌偺係暘偺侾偺柺愊偱偡丅
S2偼C傪拞怱揰偲偟偰俈m偺墌偺係暘偺侾偺柺愊偱偡丅
S3偼D傪拞怱揰偲偟偰俆m偺墌偺係暘偺侾偺柺愊偱偡丅
S4偼E傪拞怱揰偲偟偰俁m偺墌偺係暘偺侾偺柺愊偱偡丅
廬偭偰師偺幃偱寁嶼偟傑偡丅
俽亖乮侾2亄俈2亄俆2亄俁2乯乛係亊俁丏侾係 亖俇俆丏俋俆倣2
夝摎丒偦偺3
乮儁儞僱亅儉丗僽儔僢僋乯
偙偺儎僊偑
丂丂丂敿宎侾倣偺係暘偺侾墌偱摦偗傞晹暘偲
丂丂丂敿宎俈倣偺係暘偺侾墌偱摦偗傞晹暘偲
丂丂丂敿宎俆倣偺係暘偺侾墌偱摦偗傞晹暘偲
丂丂丂敿宎俁倣偺係暘偺侾墌偱摦偗傞晹暘偲傪
崌寁偡傟偽摎偊偑弌傞丅傛偭偰丒丒丒丒丒丒
丂丂丂
丂侾亊侾亊俁丏侾係亐係 亄俈亊俈亊俁丏侾係亐係 亄俆亊俆亊俁丏侾係亐係 亄俁亊俁亊俁丏侾係亐係 亖 乮侾亊侾亄俈亊俈亄俆亊俆亄俁亊俁乯亊俁丏侾係亐係 亖 俇俆丏俋係
偙傟偱
丂丂丂俇俆丏俋係偑
摎偊偲側傞丅
夝摎丒偦偺4
乮儁儞僱亅儉丗昹揷丂柧枻乯
傂傕偺挿偝俈丆傂傕偑偮側偑傟偰偄傞偔偄乮丠乯偺埵抲傪峫偊偰丆摎偼俀侾兾cm2偲側傝傑偡丏Visual Basic偱夝偒傑偟偨
Option Explicit Sub Form_Load() Picture1.BackColor = vbWhite Picture1.Scale (-2.5, 14)-(12.5, -1) Picture2.BackColor = vbWhite Picture3.BackColor = vbWhite Picture3.Picture = LoadPicture("mondai111a.gif") End Sub Sub Command1_Click() Dim Ax As Double Dim Ay As Double Dim Bx As Double Dim By As Double Dim Cx As Double Dim Cy As Double Dim Dx As Double Dim Dy As Double Dim Ex As Double Dim Ey As Double Dim Fx As Double Dim Fy As Double Dim pi As Double Dim menseki As Double ' Dx = 0 Dy = 0 Cx = 0 Cy = 6 Bx = 6 By = Cy Ax = Bx Ay = By + 2 Fx = Ax + 2 Fy = Ay Ex = Fx Ey = 0 Picture1.Cls Picture1.Line (Ax, Ay)-(Bx, By), vbBlack Picture1.Line -(Cx, Cy), vbBlack Picture1.Line -(Dx, Dy), vbBlack Picture1.Line -(Ex, Ey), vbBlack Picture1.Line -(Fx, Fy), vbBlack Picture1.Line -(Ax, Ay), vbBlack ' pi = 4 * Atn(1) Picture1.Line (Ax, Ay + 5)-(Bx, By), vbRed Picture1.Line -(Cx - 1, Cy), vbRed Picture1.Circle (Bx, By), 7, vbRed, pi * 0.5, pi menseki = 7 * 7 Picture1.Line (Fx, Fy)-(Fx + 3, Fy), vbRed Picture1.Circle (Ax, Ay), 5, vbRed, 0, pi * 0.5 menseki = menseki + 5 * 5 Picture1.Circle (Fx, Fy), 3, vbRed, pi * 1.5, pi * 2 menseki = menseki + 3 * 3 Picture1.Circle (Cx, Cy), 1, vbRed, pi, pi * 1.5 menseki = menseki + 1 * 1 menseki = menseki * 0.25 Picture2.Print "柺愊="; menseki; "兾cm2" End Sub Sub Command2_Click() Unload Me End Sub
夝摎丒偦偺5
乮儁儞僱亅儉丗teki乯
俀侾兾暯曽儊乕僩儖
儎僊偑偮側偑傟偰偄傞昍偺挿偝偑俈m側偺偱丄彫壆偺妏偵摓払偡傞偛偲偵俈仺俆仺俁 仺侾m偲摦偗傞敿宎偑抁偔側傝傑偡丅
偦傟偧傟偺昍偺挿偝偺帪偵摦偗傞斖埻偼丄侾乛係丒兾丒r2丂側偺偱丄崌寁俀侾兾 暯曽儊乕僩儖偱偡偹丅
亙偆偑偭偨摎偊亜
丂丂丂係俋兾亅俀侽暯曽儊乕僩儖
丂偙偺彫壆偑椺偊偽丄壆崻偲拰偩偗偱偱偒偰偍傝丄儎僊偑彫壆偺拞傪帺桼偵摦偒夞 傟傞偲偡傞偲 敿宎俈m偺墌撪偐傜彫壆偺柺愊傪堷偄偨斖埻偺憪傪怘傋傞偙偲偑偱偒傑偡丅乮栤戣暥 偵偼丄彫壆 偺廃傝偵憪偑惗偊偰偍傝丄彫壆偺拞偺偙偲偼彂偄偰偄側偄偺偱丄彫壆偺拞偵偼憪偼 惗偊偰偄側 偄偲峫偊傞偺偑懨摉偱偟傚偆丅乯
夝摎丒偦偺6
乮儁儞僱亅儉丗T_Tatekawa乯
彫壆偑側偗傟偽儎僊偑摦偗傞斖埻偼傂傕偺挿偝傪敿宎偲偟偨 墌偺撪晹丅 偟偐偟丄傂傕偑彫壆偺妏偵傇偮偐傞偲丄彫壆偺挿偝偺暘偩偗 傂傕偑墴偝偊偮偗傜傟偰偟傑偄丄摦偗傞斖埻偼 乮傂傕偺挿偝亅彫壆傪埻傓傂傕偺挿偝乯傪敿宎偲偡傞 墌偺撪晹偵側偭偰偟傑偆丅
墌傪係摍暘偟偰丄妏搙90搙偺愵宍傪慻傒崌傢偣偰偄偔偲丄 傑偢敿宎7m偺愵宍偑昤偗傞丅嵍懁偵摦偔偲丄彫壆偺挿偝 6m 偩偗 傂傕偑梷偊傜傟丄嵍壓偵敿宎1m偺愵宍偑昤偗傞丅 堦曽丄塃忋偵峴偔偲丄敿宎5m偺愵宍丄敿宎3m偺愵宍偑昤偗傞丅 傛偭偰媮傔傞柺愊偼
( 7x7 + 5x5 + 3x3 + 1x1 ) x 兾 /4 = 21 兾
偲側傞丅
椞堟偼揧晅偟偨恾偺嬋慄偱埻傑傟偨偲偙傠偱丄嫬奅晹傪娷傓丅
夝摎丒偦偺7
乮儁儞僱亅儉丗偺偭偙傫乯
儎僊偼敿宎俈m偺巐暘墌撪丄敿宎侾m偺巐暘墌撪丄 敿宎俆m偺巐暘墌撪丄敿宎俁m偺巐暘墌撪傪堏摦偱偒傞偺偱丄柺愊偼
丂丂丂乮係俋亄侾亄俀俆亄俋乯兾亐係亖俀侾兾乮m2乯
夝摎丒偦偺8
乮儁儞僱亅儉丗岼偺柌乯
崱夞偺栤戣偼丄巹偺戝岲偒側婳愓栤戣偱4売強偺妏偱昍偺挿偝偑丄1丄7丄5媦傃3倣 偵曄傢傝丄奺乆偺売強偱1/4墌傪昤偔偲偙傠偑億僀儞僩偱偡偹丅嵶偐偄寁嶼偼徣棯抳偟 傑偡偑丄媮傔傞柺愊偼21兾噋2偲側傝傑偡丅
夝摎丒偦偺9
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
儎僊偑怘傋傜傟傞憪抧偺柺愊偼丄敿宎偑1,3,5,7偺巐敿墌偺崌寁偵側傝傑偡丅
丂丂丂俽亖1乛4丒乮12+32+52+72乯兾亖21兾
夝摎丒偦偺10
乮儁儞僱亅儉丗僪儞僉乕乯
傑偢偼壓偺傛偆偵揰A乣F傪寛傔傑偡丏
儎僊傪偮側偄偱偄傞傂傕偺挿偝偼俈倣側偺偱丆壗傕忈奞暔偑側偗傟偽丆 儎僊偼揰B傪拞怱偲偡傞敿宎俈倣偺墌偺撪晹傪摦偔偙偲偑弌棃傑偡丅 偨偩丆暻AB偵傛傝丆儎僊偼偳傟偩偗婃挘偭偰傕忋恾偱捈慄AB傛傝壓偺晹暘偼丆 揰A傪拞怱偲偟偰敿宎侾倣偺墌偺撪晹偟偐摦偗傑偣傫丏 摨偠傛偆偵丆捈慄BC傛傝塃懁偼丆揰C傪拞怱偲偡傞敿宎俆倣偺墌丆 偝傜偵捈慄CD傛傝壓懁偼丆揰D傪拞怱偲偡傞敿宎俁倣偺墌偺撪晹偟偐摦偗傑偣傫丏傛偭偰忋偺恾偺傛偆側斖埻傪儎僊偼摦偗傑偡丏 怘傋傞偙偲偺弌棃傞憪抧偺柺愊偼丆係暘偺侾偺墌偑係偮偁傞偙偲偐傜
丂丂丂乮1亊1+7亊7+5亊5+3亊3乯亊兾亊1/4亖21兾乮m2乯丂丂丂丒丒丒乮摎乯
夝摎丒偦偺11
乮儁儞僱亅儉丗傗側偣乯
僸僣僕偝傫偑弌棃傞偩偗彫壆偐傜棧傟偰堏摦偱偒傞 婳愓傪媮傔傟偽偦偺斖埻撪偑僸僣僕偝傫偑憪傪怘傋傞偙偲偑 弌棃傞柺愊偵側傝傑偡丅
嵟弶僸僣僕偝傫偼彫壆偵増偭偰塃傊俠揰傑偱堏摦偟 偦偙偱峧偑堦攖偵側偭偰偺偱巇曽側偔壓曽柺俢傑偱堏摦偟傑偡丅 偦傟埲忋偼偙偪傜曽柺傊堏摦偱偒側偄偺偱丄巇曽側偔俠偵栠傝 崱搙偼峧偑堦攖偵挘傝偮傔偨忬懺偱俥揰傑偱堏摦 偦偙偐傜峏偵恑傫偱俫揰傑偱丄傕偆怘偄偟傫朧偩偐傜 傕偆巭傑傜偢懕偄偰俬揰傑偱堏摦 偙傟偑彫壆偐傜弌棃傞偩偗棧傟偰堏摦偱偒傞婳愓偱偡丅 偦偙偱柺愊偱偡偑
俙丏俛偼俇倣偱峧偼俈倣偩偐傜俛丏俠娫偼侾倣偵側傝傑偡丅
師偵俙丏俤娫偼俀倣側偺偱俤丏俥娫偼俆倣偵
峏偵俤丏俧娫傕俀倣側偺偱俧丏俫娫偼俁倣偵側傝傑偡丅
偦偙偱怘傋傜傟偨憪尨偺柺愊偱偡偑偦傟偧傟偺墌偺拞怱妏偼 俋侽亱側偺偱奺墌偺柺愊偼慡墌偺1/4偵側傝傑偡丅
1/4墌A.F.D偺柺愊偼
丂丂丂俈倣亊俈倣亊兾亊1/4
1/4墌E.F.H偼
丂丂丂俆倣亊俆倣亊兾亊1/4
1/4墌G.H.I偼
丂丂丂俁倣亊俁倣亊兾亊1/4
1/4墌B.C.D偼
丂丂丂侾倣亊侾倣亊兾亊1/4
偙偺崌寁偵側傝傑偡丂兾亊1/4偼嫟捠側偺偱
丂丂丂乮俈亊俈亄俆亊俆亄俁亊俁亄侾乯兾亐係亖俉係兾亐係亖俀侾兾
摎偊俀侾兾倣2乮栺俇俆丏俋俆倣2乯
夝摎丒偦偺12
乮儁儞僱亅儉丗Toru乯
奊傪彂偄偨偮傕傝偲偄偆偙偲偵偟偰丄 媮傔傞柺愊偼敿宎俈m丄侾m丄俆m丄俁m偺墌偺侾乛係傪偨偟偨傕偺偵側傞偐傜丄墌廃棪 傪兾偲偡傞偲
丂丂丂乮72+12+32+52)兾/4=21兾丂(m2)
夝摎丒偦偺13
乮儁儞僱亅儉丗夝摎儖僷儞乯
忋偺恾偺傛偆偵尨揰O偐傜儎僊偑摦偗傞斖埻偼敿宎侾倣丄俁倣丄俆倣丄俈倣偺 1/4墌偺柺愊偺憤榓偵側傞偺偱
丂丂丂兾亊乮侾2亄俁2亄俆2亄俈2乯/係亖俀侾兾 倣2
偲側傝傑偟偨丅
夝摎丒偦偺14
乮儁儞僱亅儉丗嶰妏掕婯乯
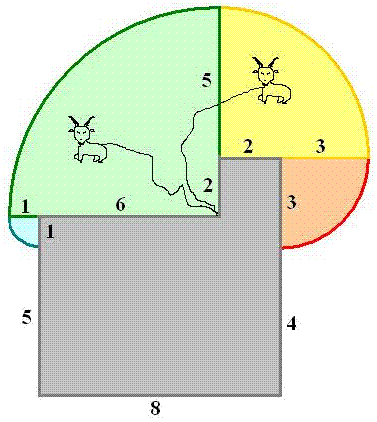
嶳梤偑憪傪怘傋傞偙偲偑偱偒傞偺偼塃恾偺拝怓偟偨係偮偺係暘墌撪偱丆偦偺柺愊偼丆
惓夝幰
teki 偺偭偙傫 僪儞僉乕 Toru 忨偺偍偠偝傫 僽儔僢僋 傗側偣 T_Tatekawa 岼偺柌 夝摎儖僷儞 昹揷丂柧枻 傒偄偨 嶰妏掕婯 栭傆偐偟偺偮傜偄偍偠偝傫
崱夞傕夝摎偺岞奐偑抶偔側偭偰偟傑偄丄偛柪榝傪偍偐偗偟偰偟傑偄傑偟偨丅怽偟栿偁傝傑偣傫丅
崱夞偵栤戣偼丄巺傪僺儞偲偼偭偰丄偦偺巺偑偼偔柺愊傪媮傔傟偽偄偄偱偡偹丅 奆偝傫偐傜恾傪採嫙偟偰偄偨偩偄偰偄傑偡捠傝丄敿宎偺堎側傞侾乛係墌傪係偮慻傒崌傢偣偨傕偺偵側傝傑偡丅
乮彫壆偺拞偵偼丄憪偑偼偊偰偄側偄偲峫偊傑偟傚偆丅乯

 E-mail
E-mail
 top
top