侾侽俋丏俀侽侽俇擭偺栤戣
侾曈偑侾侽們倣偺惓嶰妏宍偺宍傪偟偨僞僀儖偑俀侽侽俇枃偁傝傑偡丅 偙偺偆偪偺壗枃偐傪偡偒娫側偔暲傋偰惓榋妏宍傪嶌傝傑偡丅 椺偊偽俇枃偱偼丄塃偺恾偺傛偆側侾曈偑侾侽們倣偺惓榋妏宍偑偱偒傑偡丅 偱偒傞偩偗懡偔偺僞僀儖傪巊偆偲丄侾曈偑壗們倣偺惓榋妏宍傪嶌傞偙偲偑偱偒傑偡偐丅
Weekend Mathematics乛栤戣乛109偺栤戣
侾侽俋丏俀侽侽俇擭偺栤戣

侾曈偑侾侽們倣偺惓嶰妏宍偺宍傪偟偨僞僀儖偑俀侽侽俇枃偁傝傑偡丅 偙偺偆偪偺壗枃偐傪偡偒娫側偔暲傋偰惓榋妏宍傪嶌傝傑偡丅 椺偊偽俇枃偱偼丄塃偺恾偺傛偆側侾曈偑侾侽們倣偺惓榋妏宍偑偱偒傑偡丅 偱偒傞偩偗懡偔偺僞僀儖傪巊偆偲丄侾曈偑壗們倣偺惓榋妏宍傪嶌傞偙偲偑偱偒傑偡偐丅
戝恖偵栶棫偮嶼悢偺帪娫
庤搰彑楴丂娔廋
塱壀彂揦
夝摎丒偦偺1
乮儁儞僱亅儉丗傗側偣乯
偄偒側傝榋妏宍偱偼偪偲変偑攜偺摢偱偼儉僘僀偺偱 俀侽侽俇枃偺侾乛俇傪巊偭偰弌棃傞偩偗戝偒側 惓嶰妏宍傪嶌偭偰尒偨傜偳偆偐偲巚偄峫偊傑偟偨 俀侽侽俇亐俇亖俁俁係枃偵側傝傑偡 偱偐偄惓嶰妏宍傪峔惉偡傞婎杮偺惓嶰妏宍偺巊梡枃悢偼 抜乆戝偒偔側傞偵廬偭偰
丂丂丂侾丏係丏俋丏丒丒丒丒丒丒丒丒丒俁俀係枃
崯張偑尷奅偐偲偙傟偱侾俉抜偵側傝傑偡丅
偙傟偱榋妏宍傪峔惉偡傞偲偟偨傜 崌寁巊梡枃悢偼
丂丂丂俁俀係亊俇亖侾俋係係枃
曈偺挿偝偼侾俉抜側偺偱
丂丂丂侾侽亊侾俉亖侾俉侽們倣
夝摎丒偦偺2
乮儁儞僱亅儉丗偺偭偙傫乯
恾偺惓榋妏宍偼俇偮偺惓嶰妏宍偐傜偱偒偰偄傞
偦偺偆偪偺侾偮偺惓嶰妏宍偵拲栚偡傞
俀侽侽俇亐俇亖俁俁係丏俁丒丒丒偩偐傜
偦偺惓嶰妏宍偼傛傝彫偝側惓嶰妏宍偵暘妱偟偨偲偟偰
偦偺屄悢偼俁俁係屄偑尷搙偱偁傞
堦曽丄侾偮偺惓嶰妏宍偼1屄偺惓嶰妏宍偵暘妱偱偒傞
丂丂丂丂丂丂丂乂丂丂丂丂丂丂侾亄俁亖係屄偺惓嶰妏宍偵暘妱偱偒傞
丂丂丂丂丂丂丂乂丂丂丂丂丂丂侾亄俁亄俆亖俋屄偺惓嶰妏宍偵暘妱偱偒傞
丂丂丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
丂丂丂丂丂丂丂乂丂丂丂丂侾亄俁亄俆亄丒丒丒亄乮俀n亅侾乯亖n亊値屄偺惓嶰妏宍偵暘妱偱偒傞
n亊n亝俁俁係丂傪夝偄偰丂n亖侾俉
偙偺帪丄彫偝側惓嶰妏宍偺堦曈偺挿偝偼侾侽/侾俉乮cm乯偲側傞
侾侽/侾俉丗侾侽亖侾侽丗x丂傪夝偄偰丂x亖侾俉侽乮cm乯
夝摎丒偦偺3
乮儁儞僱亅儉丗T_Tatekawa乯
傑偢丆惓榋妏宍偼惓嶰妏宍俇偮偐傜惉傝棫偮帠偵拝栚偟傑偡丏
丂丂丂2006 / 6 = 334 偁傑傝 2
傛偭偰丆堦偮偺惓嶰妏宍傪嶌傞偺偵巊偊傞僞僀儖偺枃悢偼334 枃傑偱偱偡丏
師偵堦曈10cm偺惓嶰妏宍傪慻傒崌傢偣偰戝偒側惓嶰妏宍傪 嶌傞帪偵丆昁梫側僞僀儖偺枃悢傪峫偊傑偡丏
丂丂丂10cm丗1枃
丂丂丂20cm丗1+3 = 4 枃
丂丂丂30cm丗1+3+5 = 9 枃
偲偄偆嬶崌偱偡丏 偲偙傠偱偙偺惓嶰妏宍偺戝偒偝偲僞僀儖偺枃悢偺娭學偱偡偑丆 傕偲偺戝偒偝偺惓嶰妏宍偺 n 攞偺曈偺挿偝偺惓嶰妏宍傪嶌傞偵偼丆 n2 枃偺僞僀儖偑昁梫偩偲偄偆帠偑暘偐傝傑偡丏側偤側傜丆
1 + 3 + 5 + ... + (2n-1) = (2-1) + (4-1) + (6-1) + ... + (2n-1) = 2* n(n-1)/2 -n = n2
偩偐傜偱偡丏偮傑傝丆
丂丂丂n2 < 334
傪挻偊側偄嵟戝偺 n 偑丆偙偺栤戣偱嶌傞帠偺弌棃傞嵟戝偺 惓嶰妏宍偺戝偒偝傪寛傔傑偡丏
丂丂丂182 = 324, 192 = 361
側偺偱丆嵟戝偺 n 偼 18 偱偡丏 偙偺帪偺惓嶰妏宍偺堦曈偺挿偝偼 180cm丏偮傑傝惓榋妏宍偺 堦曈偺挿偝偼嵟戝偱 180cm 偱偡丏
夝摎丒偦偺4
乮儁儞僱亅儉丗僪儞僉乕乯
亙夝摎亜
惓榋妏宍偼丄俇偮偺惓嶰妏宍偐傜弌棃偰偄傑偡丅
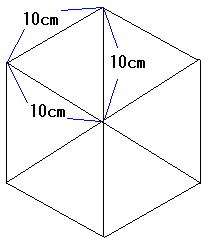
栤戣暥偱偼堦曈偑10乮們倣乯偺傕偺偺恾偑梌偊傜傟偰偄傑偡偑丄 堦曈偺挿偝偑10値乮們倣乯偺傕偺偵偮偄偰傕丄戝偒偔傒傟偽俇偮偺惓嶰妏宍偐傜弌棃偰偄傑偡丅
恾丗堦曈偺挿偝偑10値乮們倣乯偺惓榋妏宍
忋偺恾偱丄愒慄偱昤偐傟偨晹暘偑戝偒偔尒傟偽侾偮偺惓嶰妏宍側傢偗偱偡丅 偙偺惓嶰妏宍偵巊傢傟傞僞僀儖偺悢傪尋媶偡傟偽丄偁偲偼偦傟傪俇攞偡傟偽偄偄傢偗偱偡偹丅
暘偐傝傗偡偔偡傞偨傔丄彮偟戝偒傔偺恾偱峫偊傑偟傚偆丅 忋偺恾偼堦曈偺挿偝偑60們倣偺惓嶰妏宍偱偡丅 傛偔尒偰傒傞偲丄堦斣忋偺抜偵偼1枃丄俀抜栚偵偼3枃丄俁抜栚偵偼5枃丄係抜栚偵偼7枃丄俆抜栚偼9枃丄俇抜栚偼11枃偺僞僀儖偑巊傢傟偰偄傑偡丅 婯懃揑偱偡偹丅偮傑傝丄値抜栚偼2値-1枃乮婏悢乯側傫偱偡丅 偙偺壓偵壗抜愊傒廳偹偰傕摨偠側偺偼丄彮偟幚尡偟偰傒傞偲暘偐傞偲巚偄傑偡丅 傛偭偰丄堦曈偺挿偝偑10値乮們倣乯偺惓嶰妏宍傪嶌傞偵偼丄値抜偺僞僀儖偑昁梫側偺偱
丂丂丂1+3+5+丒丒丒+乮2値-1乯亖値2乮枃乯
偺僞僀儖偑昁梫偵側傝傑偡丅 乮忋偺懌偟嶼偼丄弶崁侾丆枛崁2値-1丆崁悢値偺摍嵎悢楍偺榓偱偡偐傜丄娙扨偵寁嶼偱偒傑偡丅乯 偲偄偆偙偲偱丄堦曈偺挿偝偑10値乮們倣乯偺惓榋妏宍傪嶌傞偵偼丄 偙偺惓嶰妏宍偑俇屄偁傟偽傛偄偺偱丄6亊値2乮枃乯偺僞僀儖偑昁梫偵側傝傑偡丅 偙傟偱弨旛偼廔傢傝傑偟偨丅 俀侽侽俇枃偺僞僀儖偑偁傝傑偡偐傜丄偦傟埲壓偺枃悢偱6亊値2偺宍偵昞偣傞嵟戝偺惍悢傪尒偮偗傟偽偄偄傢偗偱偡丅寢壥偩偗偄偆偺傕偁傟偱偡偐傜丄偪傖傫偲偦偺傛偆側値傪尒偮偗偰傒傑偟傚偆丅
丂丂丂2006亖6亊値2
偲偍偔偲丄
丂丂丂値2亖2006/6亖334.333丒丒丒
丂亪 値佮18.28
傛偭偰丄俀侽侽俇埲壓偱6亊値2偺宍偵昞偣傞嵟戝偺惍悢偼丄値亖18偺偲偒偱
丂丂丂6亊182亖1944
偲側傝傑偡丅偮傑傝丄俀侽侽俇枃偺僞僀儖傪巊偭偰嶌傟傞嵟戝偺惓榋妏宍偼堦曈180們倣丂丂丒丒丒乮摎乯
偪側傒偵丄6亊192亖2166側偺偱丄2165擭傑偱偼偙偺栤戣偺摎偼摨偠偱偡乮徫乯
夝摎丒偦偺5
乮儁儞僱亅儉丗teki乯
摎偊丂丂侾俉侽們倣
嶌傜傟傞惓榋妏宍偺侾曈偺挿偝偼丄偳偆峫偊偰傕尦偺惓嶰妏宍偺侾曈偺挿偝 偺攞悢偵側傝傑偡丅 偙傟偲丄嵟彫偺惓榋妏宍偺柺愊偑惓嶰妏宍偺柺愊偺俇攞偱偁傞偙偲偐傜丄
丂丂丂俀侽侽俇亐俇亖俁俁係丏俁俁丒丒丒
偱嵟彫偺惓榋妏宍偺柺愊偺俁俁係攞偺柺愊傪 帩偮惓榋妏宍傑偱嶌傟傞壜擻惈偑偁傝傑偡丅 惓嶰妏宍偱傕惓榋妏宍偱傕丄偦偺柺愊偼侾曈偺挿偝偺俀忔偵斾椺偡傞偺 偱丄嶌傟傞惓榋妏宍偺侾曈偺挿偝偼丄
丂丂丂併俁俁係丏俁俁丒丒亊侾侽亖侾俉俀丏俉俈丒丒丒
埲壓偲側傝傑偡丅 偙傟偑侾侽偺攞悢偲側傞嵟戝偼侾俉侽們倣偱偡偹丅 偱傕丄幚嵺嶌傟傞偐偳偆偐専徹偟偰偄傑偣傫丅乮偱傕丄嵟彫偺惓榋妏宍偺廃傝 偵惓嶰妏宍傪晘偒媗傔傟偽偱偒偦偆偱偡丅乯 偙偺偲偒巊梡偡傞僞僀儖偺枃悢偼侾俉亊侾俉亊俇亖侾俋係係枃偱丄俇俀枃梋傝傑偡丅
亙栤戣亜
儚僀儎乕儘乕僾偑俀侽侽俇杮偁傝傑偡丅 偙傟傪榋妏宍偺宍偵懇偹偰懢偄儘乕僾傪嶌傝偨偄偺偱偡偑丄嵟戝偱 壗杮偺儘乕僾傪巊偭偨傕偺偑偱偒傞偱偟傚偆偐丠 偙偺栤戣偼丄堦斒偵乽桳恈榋妏悢乿偲屇偽傟傞悢傪峫偊傞傢偗偱偡偑 偙偺堦斒宍偼丄
丂丂丂侾亄嚁値亖侾亄値丒乮値亄侾乯/俀丂偲側傝傑偡丅
俀侽侽俇杮偺儘乕僾偱偼丄値亖俇俀偑嵟戝偱丄侾俋俆係杮偺儘乕僾傪巊偭偰 榋妏宍偺儘乕僾傪嶌傟傑偡丅
崱寧偺栤戣偺応崌偼丄偙傟偲崿摨偟偑偪偱偡偑丄巹偺夝摎偵偁傞傛偆 偵柺愊偱峫偊側偄偲娫堘偊傑偡偹丅
夝摎丒偦偺6
乮儁儞僱亅儉丗僆儎僕乯
堦曈丂侾侽値乮們倣乯偺惓嶰妏宍偺屄悢偼丄丂値俀屄
偟偨偑偭偰惓俇妏宍偺屄悢偼丂俇仏値俀屄
戣堄傛傝丂丂俇仏値俀亙亖俀侽侽俇丂傪値傪帺慠悢偺忦審偱夝偔偲
値亖侾俉丂偟偨偑偭偰堦曈丂侾侽値亖侾俉侽丂乮們倣乯丂
夝摎丒偦偺7
乮儁儞僱亅儉丗kiyo乯
6*n2亝2006丂丂 n偼帺慠悢丅
忋幃傪枮偨偡嵟戝偺n偼18丅
偟偨偑偭偰丄嵟戝偺侾曈偼180們倣偱偡丅
偙偺偲偒巊偆僞僀儖偺悢偼丄1944屄丅
夝摎丒偦偺8
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂惓榋妏宍偺堦曈偺挿偝偼侾俉侽們倣偱偡
傾僀僐儞偑侾曈侾侽cm偺惓嶰妏宍俀枃傪暲傋偰惓嶰妏宍傪嶌傞偵偼壗枃巊偆偐丄 侾曈侾侽cm偺惓嶰妏宍俁枃傪暲傋偰惓嶰妏宍傪嶌傞偵偼壗枃巊偆偐怓乆峫偊偰偄傑偡丅 偦偟偰壓偺幃偵傪巊偄寁嶼偟傑偟偨丅
1曈偑1枃偺俇妏宍偺巊梡僞僀儖枃悢偼俇枃丄2枃偺帪偼俀係枃丄俁枃偼俆係枃丄 4枃偼俋俇枃巊梡偟傑偡丅
巊梡枃悢偼俀侽侽俇枃埲壓側偺偱師偺悢楍偵傛傞寁嶼幃偱媮傔傑偡丅
丂丂丂俶俀亊俇亝俀侽侽俇
丂丂丂俶亝併2006/6
丂丂丂俶亝侾俉丏俀俉係俈乧
俶偼惍悢側偺偱1曈偼侾俉枃偲側傝傑偡丅廬偭偰侾俉亊侾侽亖侾俉侽們倣
巊梡僞僀儖悢偼侾俉俀亊俇亖侾俋俋係枃偱偡丅
夝摎丒偦偺9
乮儁儞僱亅儉丗夝摎儖僷儞乯
惓榋妏宍偼俇偮偺嶰妏宍偐傜側傞偺偱丄
堦曈偑 10cm偺惓榋妏宍偱巊傢傟傞惓嶰妏宍偺枃悢偼 侾亊俇枃 20cm 係亊俇=俀係枃 30cm 俋亊俇=俆係枃 40cm 侾俇亊俇=俋俇枃 丗 丗 n cm 値俀亊俇亖俇丒n俀枃
俇丒値俀亝俀侽侽俇亖俁俁係丒俇亄俀 偲側傞丅
値偼帺慠悢側偺偱丄値俀亝丂俁俁係丂偲側傞値偺嵟戝抣傪媮傔傟偽傛偄丅
丂丂丂侾俉俀亖俁俀係
丂丂丂侾俋俀亖俁俇侾丂傛傝
丂丂丂侾俉俀亙俁俁係亙侾俋俀丂偱偁傞偐傜値亖侾俉丂偑嵟戝抣偲側傞丅
傛偭偰丄俇丒侾俉俀亖俇丒俁俀係亖侾俋係係枃
侾俋係係枃偲側傝傑偟偨丅
夝摎丒偦偺10
乮儁儞僱亅儉丗俰俽儈儖乯
幚嵺恾偵偟偰傒傑偡偲丆僞僀儖偺1曈偑10們倣側偺偱丆 1曈偑10們倣偺惓榋妏宍偵偼僞僀儖3亊2亖6屄丆20們倣偺惓榋妏宍偵偼僞僀儖12亊2 亖24屄丆30們倣偺惓榋妏宍偵偼27亊2亖54屄偺僞僀儖偑昁梫偱偡丏偙傟傜傪丆僞僀儖 堦偮堦偮偱傒傞偲
10們倣偺帪 乮1+2乯亊2 亖6 20們倣偺帪 乮2+3+3+4乯亊2 亖24 30們倣偺帪 乮3+4+4+5+5+6乯亊2 亖54
偲側偭偰偍傝丆堦斒壔偡傞偲丄10倠們倣偺帪
乷乮倠+倠+1乯+乮倠+1+倠+2乯+乮倠+2+丒丒丒丒+乮倠+倠-1+倠+倠乯乸亊2丒丒?偲側傞丏
?偼
乷倠+俀乮倠+1+倠+2+丒丒丒+倠+倠-1乯+倠+倠乸亊2 亖 乷3倠+2倠乮倠-1乯+倠乮倠-1乯乸亊2 亖 6倠2
廬偭偰丆2006亞6倠2偲側傞倠偺嵟戝抣偼18
丂丂丂摎偊丗1曈偑180們倣偺惓榋妏宍偱丆巊梡偡傞僞僀儖偺悢偼1944枃
夝摎丒偦偺11
乮儁儞僱亅儉丗抴鍋偺憙忛乯
俇屄偺惓嶰妏宍偱侾屄偺惓榋妏宍傪峔惉偡傞偲偒丄偙偺惓嶰妏宍傪峔惉僺乕僗偲尵偄昞偡帠偵偟丄侾曈偑10噋 偺惓嶰妏宍傪婎杮僺乕僗偲偟傑偡丅2006屄埲撪偺婎杮僺乕僗偱丄嵟戝偺峔惉僺乕僗傪6屄嶌傟偽傛偄傢偗偱偡丅
侾偮偺峔惉僺乕僗偑丄値 抜偺婎杮僺乕僗偺廳側傝偱弌棃偰偄傞偲偒丄壓偺晄摍幃傪枮偨偡嵟戝偺値傪尒偮偗傞帠偵偟傑偟傚偆丅
丂丂丂
丂丂丂丂嵟戝偺値亖侾俉
廬偭偰丄侾曈180噋 偺嵟戝偺惓榋妏宍傪嶌傞偙偲偑弌棃傑偡丅 嶼悢偺栤戣偩偲尵偭偰偄傞偺偵丄堘斀偱偡偹丅
夝摎丒偦偺12
乮儁儞僱亅儉丗岼偺柌乯
10噋偺惓嶰妏宍傪婎杮偲偡傞偲丄堦曈偺挿偝偺擇忔攞偱柺愊偼憹壛偡傞丅 偦偙偱10噋偺N攞傪峫偊傞偲柺愊偼N2攞偲側傞丅 惓榋妏宍偼偙偺惓嶰妏宍6屄偐傜側傞偺偱丄憤柺愊偼6N2偲側傞丅 枖丄偙偺柺愊偼堦曈10噋偺惓嶰妏宍偺枃悢傕昞偟偰偄傞偺偱丄2006傛傝彫偝側嵟戝偺N傪媮傔傟偽椙偄丅
丂丂丂6N2亝2006
傪夝偔偲N亖18偲側傞丅懄偪媮傔傞傕偺偼堦曈180噋偺惓榋妏宍偱偁傞丅
夝摎丒偦偺13
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
偱偒偁偑偭偨惓俇妏宍偺侾曈偺挿偝偼丄侾侽cm偺惍悢攞偵側傝傑偡丅
偦偺侾曈偲拞怱偲偱寛傑傞惓俁妏宍傪峫偊傑偡丅乮嵍偺恾乯
偦偺惓俁妏宍偺僞僀儖偺屄悢傪墶偵悢偊偰傒傞偲塃偺恾偺傛偆偵側偭偰偄傑偡丅
僞僀儖偑値抜愊傒廳側偭偰偄傞偲偡傞偲丄偦偺屄悢偼丄
丂丂丂侾亄俁亄俆亄ゥゥゥ亄(俀n亅侾)亖値2
偱偡丅 憡帡偺娭學偵偁傞恾宍偺柺愊偼懳墳挿偝偺暯曽偵斾椺偡傞偺偱偡偖偵値2屄偲傕峫偊傜傟傑偡丅
偩偐傜侾曈偑侾侽値cm偺惓俇妏宍偱偼丄俇値^2屄偺僞僀儖偑昁梫偱偡丅
丂丂丂俇値2丂亝丂俀侽侽俇
傪夝偔偲丄嵟戝偺惍悢偼丄値亖侾俉偱偡丅
偩偐傜丄侾曈偺挿偝偼丄侾俉侽cm偲側傝傑偡丅
乮梋傝偼俇俀屄偱偡乯
夝摎丒偦偺14
乮儁儞僱亅儉丗Toru乯
侾曈侾侽cm偺僞僀儖傪巊偆偐傜丄惓榋妏宍偺侾曈偼10 cm偺帺慠悢攞偲側傝 偙偺応崌丄侾曈侾侽cm偺僞僀儖偱偡偒娫側偔偆傔傞偙偲偑偱偒傞丅 侾曈侾侽N cm偺惓榋妏宍偺柺愊偼侾曈侾侽cm偺傕偺偺N2攞 傛偭偰6xN2屄偺僞僀儖偑昁梫
丂丂丂6x182=1944
丂丂丂6x192=2166
傛傝 1曈丂180cm丂偺惓榋妏宍偑壜擻
夝摎丒偦偺15
乮儁儞僱亅儉丗嶰妏掕婯乯
恾偺傛偆偵丆惓榋妏宍偼摍曈偺惓嶰妏宍6枃偐傜嶌傜傟傞丅1曈偑 n偺惓嶰妏宍偼丆1曈1偺惓嶰妏宍(亖扨埵惓嶰妏宍乯n2 枃偐傜嶌傜傟偐傜丆1曈n偺惓榋妏宍偼6n2枃偺扨埵惓嶰妏宍偐傜惉傞丅2006 埲壓偺6 n2 偺嵟戝抣偼丆n亖18 偺偲偒偺 1944丅
傛偭偰丆1曈10cm偺惓嶰妏宍2006枃偐傜嶌傞偙偲偑偱偒傞惓榋妏宍偺1曈偼180cm丅
惓夝幰
teki 忨偺偍偠偝傫 偺偭偙傫 僪儞僉乕 傗側偣 岼偺柌 嶰妏掕婯 Toru T_Tatekawa 僆儎僕 俰俽儈儖 栭傆偐偟偺偮傜偄偍偠偝傫 夝摎儖僷儞 kiyo 抴鍋偺憙忛
俇曽岦偵懳徾惈傪帩偭偰偄傞恾宍側偺偱丄偦偺1/6傪峫偊偰偄偗偽偄偄偙偲偵側傝傑偡丅 偦偆傗偭偰峴偒拝偄偨幃乽6n2亝2006乿傪挱傔傞偲丄 俀師尦偵峀偑傞恾宍偩偐傜丄偦傝傖偦偆偩傛偹偲柇偵擺摼偟傑偡丅
偙偺幃傪枮偨偡嵟戝偺惍悢偼n=18偱丄偙偺偲偒巊梡偡傞僞僀儖偺悢偼1944枃丄62枃梋傞偙偲偵側傝傑偡丅 偮傑傝丄2006偲偄偆悢偺昁慠惈偼側偄偲偄偆偙偲偱偡丄偛傔傫側偝偄丅

 E-mail
E-mail
 top
top