夝摎丒偦偺1
乮儁儞僱亅儉丗傗側偣乯
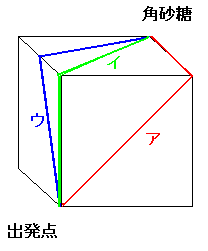
柺傪揥奐偡傟偽傛偔傢偐傝傑偡
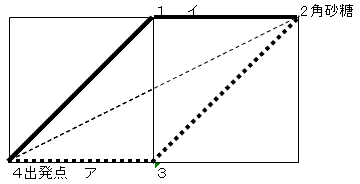
傾偺僐乕僗偼嶰妏宍係丏俁丏俀偺俀曈傪捠傝丄僀偺僐乕僗傕摨偠傛偆偵嶰妏宍係丏侾丏俀偺俀曈傪捠傝傑偡丅
僂偺僐乕僗偼嵟抁偺応崌嶰妏宍係丏俁丏俀傑偨偼係丏侾丏俀丏偺侾曈傪捠傝傑偡丅
嶰妏宍偺掕媊偐傜俀曈偺挿偝偺崌寁偼巆傝偺侾曈傛傝挿偄偺偱嵟抁僐乕僗偼僂偱偡偹丄暿偵曈侾丏俁偺拞揰傪捠夁偟側偔偰傕抁偄偺偱偡偑愢柧偑挿偄偺偱傗傔偱偡側丅
偍摎偊偼僂偺媋偝傫偑堦斣愭偵妏嵒摐偵摓拝偱偡側

夝摎丒偦偺2
乮儁儞僱亅儉丗Magi乯
1. 丂棫曽懱偺堦曈偺挿偝傪 a 偲偡傞丅
傾偲僀偺僐乕僗偼丄嫟偵棫曽懱偺堦曈偲堦柺偺懳妏慄傪捠傞偺偱丄偙偺擇偮偺嫍棧偼
摍偟偄丅
嫍棧偼丄a+(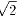 乯a
= (1+
乯a
= (1+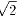 )a 偲側傞丅
)a 偲側傞丅
僂偺僐乕僗偵偮偄偰偼丄棫曽懱傪揥奐偟偰峫偊傞丅
偮傑傝丄僂偺嫍棧偼廲偲墶偺挿偝偑 a 偲 俀a 偺挿曽宍偺懳妏慄偺挿偝偵摍偟偄丅
偡側傢偪丄嫍棧偼併乮a2+(2a)2乯 = 乮併俆乯a 偲側傞丅
(併俆) 亙 (1+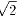 )丄
偟偨偑偭偰妏嵒摐偵嵟弶偵偨偳傝拝偔偺偼僂偺僐乕僗偺傾儕偱
偁傞丅
)丄
偟偨偑偭偰妏嵒摐偵嵟弶偵偨偳傝拝偔偺偼僂偺僐乕僗偺傾儕偱
偁傞丅

夝摎丒偦偺3
乮儁儞僱亅儉丗僯僩儘乯
侾丏傾偲僀偼摨偠嫍棧偵側傞偺偱丄僐僐偱偼僀偲僂偺僐乕僗傪斾妑偟傑偡丅
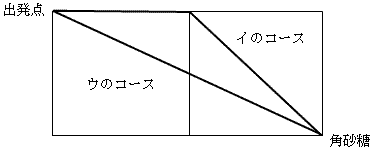
奊偵偡傞偲娙扨偵敾抐偱偒傑偡偹丅
丂丂夝摎亜僂

夝摎丒偦偺4
乮儁儞僱亅儉丗嶰妏掕婯乯
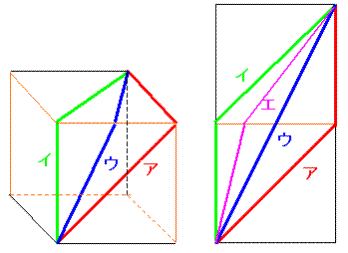
乮恾傪彂偒傗偡偔偡傞偨傔 僂 傪摦偐偟傑偟偨丅乯
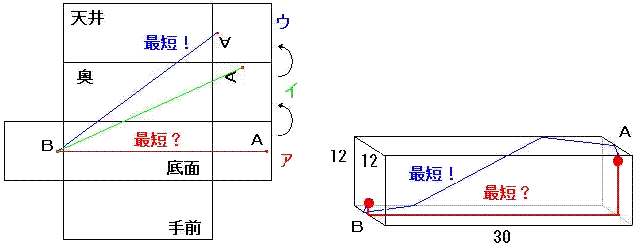
塃懁偺揥奐恾偐傜傢偐傞傛偆偵宱楬偑嵟傕抁偄偺偼丂僂 乧乵摎乶
乮傾丆僀偼嶰妏宍偺2曈丆僂偼1曈乯
悢妛偲偟偰偺夝偼埲忋偱偟傚偆偑丆巹偼塃偺 僄 傪惓夝偲偟偨偄偱偡丅
棟桼偼丆偁傝偼敔偺庤慜偺柺傪曕偄偰偄傞偲偒偼乮妏嵒摐偑尒偊側偄偺偱乯
傢傝偲偺傫傃傝曕偔偑丆忋柺偵擖傝妏嵒摐傪尒偮偗傞偲乽僗儚僢乿偲堦栚嶶偵憱傝弌偡丅
偡傞偲丆僄 偑嵟抁帪娫偵側傞偙偲傪帵偡偙偲偑偱偒傑偡丅岝偺孅愜偲摨偠尨棟偱偡丅

夝摎丒偦偺5
乮儁儞僱亅儉丗昹揷丂柧枻乯
栤戣侾
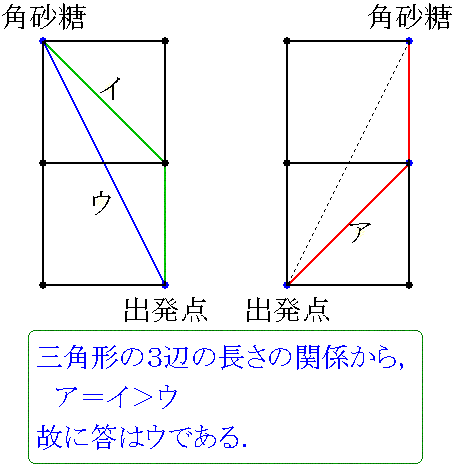
栤戣俀
懳徧惈偐傜丆墱偺柺乮侾俀亊俁侽乯偼巊傢側偔偰傛偄丏
偡傋偰偺応崌傪恾帵偟丆偦傟偧傟偺応崌偺俙俛偺挿偝傪媮傔丆偦偺嵟彫抣傪摎偲偡傞丏
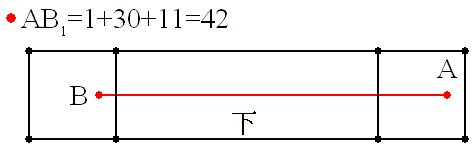
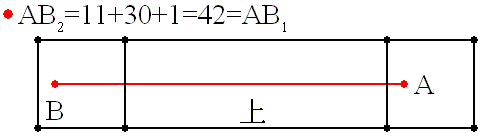
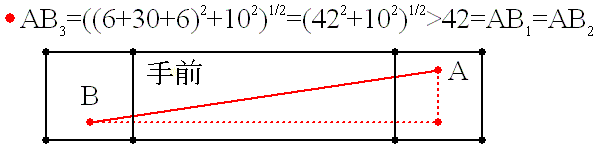
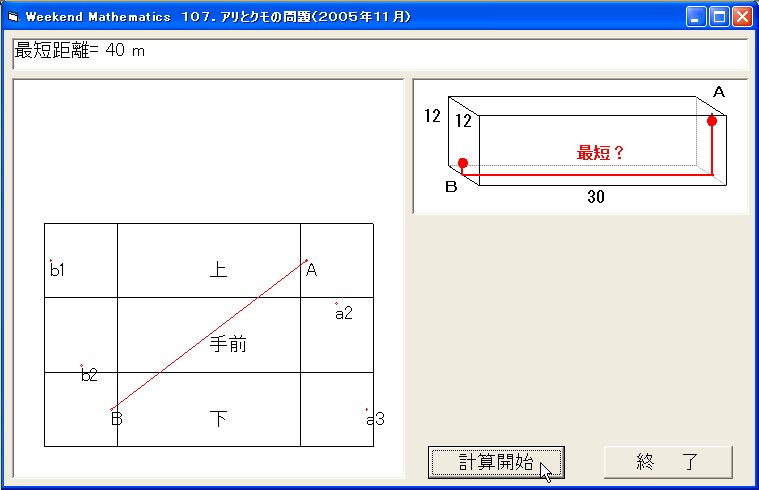
屘偵嵟抁嫍棧偼係侽倣偱偁傞丏
偙偺峫偊曽傪棙梡偟偰丆Visual Basic偺僾儘僌儔儉傪嶌偭偰傒偨丏
埲壓偺捠傝偱偁傞丏寢壥偼摨偠傕偺偲側偭偨丏
乮僐僺乕仌揬傝晅偗偡傞嵺偼丆慡妏偺嬻敀傪敿妏偵偟側偔偰偼側傝傑偣傫乯
Option Explicit
Sub Form_Load()
Dim waku As Double
waku = 5
Picture1.Scale (-waku, 12 + 30 + 12 + waku)-(12 + 30 + 12 + waku, -waku)
Picture1.BackColor = vbWhite
Picture2.BackColor = vbWhite
Picture2.Picture = LoadPicture("mondai107b.gif")
Picture3.BackColor = vbWhite
End Sub
Sub Command1_Click()
Dim Ax(3) As Double
Dim Ay(3) As Double
Dim Bx(3) As Double
Dim By(3) As Double
Dim Axx As Double
Dim Ayy As Double
Dim Bxx As Double
Dim Byy As Double
Dim min As Double
Dim nagasa As Double
Dim ten_hankei As Double
Dim j1 As Integer
Dim j2 As Integer
Dim j3 As Integer
'
Ax(1) = 12 + 30 + 1
Ay(1) = 2 * 12 + 6
Ax(2) = 12 + 30 + 6
Ay(2) = 12 + 11
Ax(3) = 12 + 30 + 11
Ay(3) = 6
Bx(1) = 1
By(1) = 2 * 12 + 6
Bx(2) = 6
By(2) = 12 + 1
Bx(3) = 11
By(3) = 6
min = 100000
ten_hankei = 0.15
For j1 = 1 To 3
For j2 = 1 To 3
nagasa = Sqr((Bx(j2) - Ax(j1)) * (Bx(j2) - Ax(j1)) + (By(j2) - Ay(j1)) * (By(j2) - Ay(j1)))
If min > nagasa Then
min = nagasa
Axx = Ax(j1)
Ayy = Ay(j1)
Bxx = Bx(j2)
Byy = By(j2)
Picture3.Cls
Picture3.Print "嵟抁嫍棧="; min; "m(?)"
End If
Call sakuzu
For j3 = 1 To 3
Picture1.Circle (Ax(j3), Ay(j3)), ten_hankei, vbRed
Picture1.Circle (Bx(j3), By(j3)), ten_hankei, vbRed
Picture1.CurrentX = Ax(j3)
Picture1.CurrentY = Ay(j3)
Picture1.Print "A"; strr(j3)
Picture1.CurrentX = Bx(j3)
Picture1.CurrentY = By(j3)
Picture1.Print "B"; strr(j3)
Next j3
Picture1.Line (Axx, Ayy)-(Bxx, Byy), vbGreen
Picture1.Line (Ax(j1), Ay(j1))-(Bx(j2), By(j2)), vbRed
Call wt
Next j2
Next j1
Picture3.Cls
Picture3.Print "嵟抁嫍棧="; min; "m"
Call sakuzu
For j1 = 1 To 3
Picture1.Circle (Ax(j1), Ay(j1)), ten_hankei, vbRed
Picture1.Circle (Bx(j1), By(j1)), ten_hankei, vbRed
Picture1.CurrentX = Ax(j1)
Picture1.CurrentY = Ay(j1)
If Axx <> Ax(j1) Or Ayy <> Ay(j1) Then
Picture1.Print "a"; strr(j1)
Else
Picture1.Print "A"
End If
Picture1.CurrentX = Bx(j1)
Picture1.CurrentY = By(j1)
If Bxx <> Bx(j1) Or Byy <> By(j1) Then
Picture1.Print "b"; strr(j1)
Else
Picture1.Print "B"
End If
Next j1
Picture1.Line (Axx, Ayy)-(Bxx, Byy), vbRed
End Sub
Sub Command2_Click()
Unload Me
End Sub
Sub sakuzu()
Dim j As Integer
Picture1.Cls
For j = 0 To 3
Picture1.Line (0, j * 12)-(12 + 30 + 12, j * 12), vbBlack
Next j
Picture1.Line (0, 0)-(0, 3 * 12), vbBlack
Picture1.Line (12, 0)-(12, 3 * 12), vbBlack
Picture1.Line (12 + 30, 0)-(12 + 30, 3 * 12), vbBlack
Picture1.Line (12 + 30 + 12, 0)-(12 + 30 + 12, 3 * 12), vbBlack
Picture1.CurrentX = 12 + 15
Picture1.CurrentY = 2 * 12 + 6
Picture1.Print "忋"
Picture1.CurrentX = 12 + 15
Picture1.CurrentY = 12 + 6
Picture1.Print "庤慜"
Picture1.CurrentX = 12 + 15
Picture1.CurrentY = 6
Picture1.Print "壓"
End Sub
Sub wt()
Dim j As Long
For j = -50000000 To 50000000
Next j
End Sub
Private Function strr(ByVal n As Integer) As String
strr = Right(Str(n), Len(Str(n)) - 1)
End Function

夝摎丒偦偺6
乮儁儞僱亅儉丗俰俽儈儖乯
偦傟偧傟偺敔傪揥奐偟偰丆揰偐傜揰偵捈慄揑偵峴偔偺偑嵟抁偱偡偺偱丆妏嵒摐偺栤戣
偼僂偲巚偄傑偡丏
栤2偺摎偊偼40倣偱偡偹丏
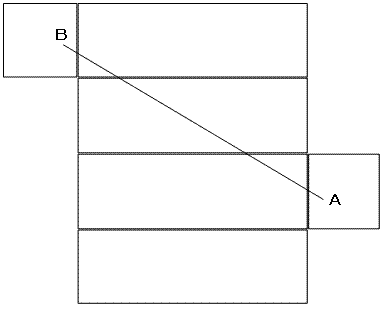
尞偑揥奐恾偱偁傞偙偲偼壗偲側偔傢偐偭偰偄傑偟偨偑丆傗傜傟偨偲尵偆姶偠偱偡丏僋
儌偼揤堜偵僴僄偼彴偵嬤偄応強偵偄傞傢偗偱偡偐傜丆嵟傕嬤偔側傞傛偆側揥奐恾傪嶌
惉偟丆偦傟傪捈慄偱寢傋偽嵟抁側傢偗偱偡偹丏12倣傗30倣丆1倣偲偄偭偨悢帤傕嵟屻
偵併1600偵側傞傛偆偵嶌傜傟偰偄偨偺偱偡偹丏摢偺懱憖偵側傝傑偟偨丏

夝摎丒偦偺7
乮儁儞僱亅儉丗夝摎儖僷儞乯
偙傫偵偪偼丄儁儞僱乕儉夝摎儖僷儞偱偡丅
挿曽宍偺栤戣偵堷偒懕偒
傾儕偲僋儌偺栤戣傪夝偄偰傒傑偟偨丅
侾丄僂偺傾儕偱偡丅
棫曽懱偺堦曈偺挿偝傪a偲偡傞偲丄
僂偼a亊併5丂丄傾偲僀偼a亄a亊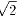 亖a亊乮侾亄
亖a亊乮侾亄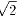 )丄偲側傞偨傔丄
)丄偲側傞偨傔丄
僂偺宱楬偺曽偑抁偄偐傜偱偡丅
俀丄係侽倣偱偡丅
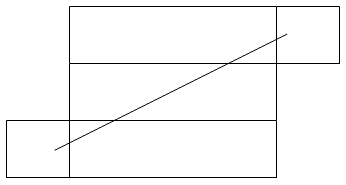
揧晅恾偺條偵俆偮偺柺傪捠傞儖乕僩偱40m偲側傝傑偟偨丅
丂併乷乮侾亄俁侽亄侾乯亊乮侾亄俁侽亄侾乯亄乮俇亄侾俀亄俇乯亊乮俇亄侾俀亄俇乯乸倣
亖併乮俁俀亊俁俀亄俀係亊俀係乯倣
亖係侽倣

夝摎丒偦偺8
乮儁儞僱亅儉丗僪儞僉乕乯
侾丏傛偔恾傪尒傞偲丄傾偲僀偼慡偔摨偠挿偝偺摴偵側偭偰偄傑偡丅
棫曽懱傪側偟偰偄傞惓曽宍偺懳妏慄偲曈偺挿偝偺榓偱偡偹丅
乽嵟弶偵拝偔偺偼偳偺偁傝偩傠偆偐丠乿偲暦偐傟偰偄傞偺偱丄撉傒偑偄偄恖偼乽偳偆偣摎偼僂側傫偱偟傚丅摨拝側傫偰柺敀偔側偄傕傫偹丅乿 偲巚偆偱偟傚偆丅幚嵺偦傟偱惓夝側傫偱偡偗偳丄偦傟偱偼摎偵側偭偰偄側偄偺偱寉偔夝愢丅
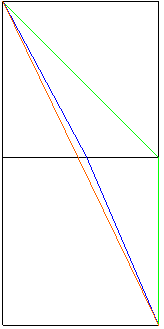
棫曽懱傪揥奐偟偰傒傑偟傚偆丅
偡傞偲僀偲僂偺僐乕僗偼摨偠俀柺偵彂偔偙偲偑弌棃傑偡丅
堦斣抁偄僐乕僗偼僗僞乕僩偲僑乕儖傪堦捈慄偵寢傫偩宱楬乮僆儗儞僕乯側偺偱丄
偦偙偐傜偺僘儗偑偳傟偩偗偐偱嫍棧傪應傞偙偲偑弌棃傑偡丅
堦墳僂偺宱楬偑惓曽宍偺曈偺拞揰傪捠偭偰偄傞偲偄偆忦審偼柍偄偺偱丄
彮偟愜傟嬋偑偭偨恾偵偟偰傒傑偟偨偑丄僀偲僂偺偳偪傜偺僐乕僗偑抁偄偐偼姶妎偱暘偐傝傑偡傛偹丠
僂偺曽偑抁偄傫偱偡丅徻偟偄寁嶼偼徣偒傑偡乮暋嶨側寁嶼傪偐偄偰傕偍傕偟傠偔側偄偺偱乯丅
崱偼丄嵟抁宱楬乮捈慄乯偺搑拞偺揰傪偮傑傫偱堷偭挘偭偨偲偒丄
僀偺傎偆偑懡偔堷偭挘偭偨偺偱挿偔側偭偰偟傑偆丄偲偄偆姶偠偵棟夝偟偰偍偒傑偟傚偆丅
俀丏捈曽懱偺晹壆傪僷僞僷僞偲揥奐偟偰暯柺偵偟偨偲偒丄
俙揰偲俛揰傪捈慄偱寢傫偩応崌偑嵟抁偵側傞偺偼柧敀偱偡丅
偙偙偱丄俙揰偲俛揰傪寢傇慄暘偑搑拞壗屄偺挿曽宍傪偄偔偮宱桼偡傞偐偑栤戣偵側傝傑偡丅
係偮偺挿曽宍傪宱桼偡傞応崌偼丄堦曈偺挿偝側偳偺娭學偐傜捈慄宱楬偑寢傋傑偣傫丅丂
俆偮埲忋偺挿曽宍傪宱桼偡傞応崌偼丄宱楬偑挿偡偓偰42倣埲忋偵側偭偰偟傑偄丄
栤戣暥偺恾偺応崌傛傝傕挿偔側偭偰偟傑偄傑偡丅
偲偄偆傢偗偱丄宱桼偡傞挿曽宍偺悢偼侾偮丄俀偮丄俁偮偺偳傟偐偵側傝傑偟偨丅
偦偺拞偱扵偟偰傒傞偲丄師偺恾偑戣堄偺応崌偩偲暘偐傝傑偡丅
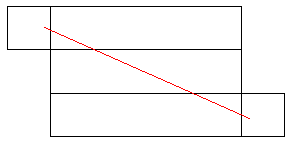
偙偺恾偑嵟彫偺応崌偱偡偹丅
挿偝偼偪傚偆偳40倣偱偡丅

夝摎丒偦偺9
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
崱夞傕傾僀僐儞偑峫偊偰偔傟傑偟偨丅
摎偊丅
侾丏僂偑嵟弶偵摓拝偟傑偡丅
俀丏嵟抁僐乕僗偼係侽倣偱偡丅
侾丏 傾偲僀偼摨偠嫍棧偱偡丅
棫曽懱偺堦曈傪10們倣偲偡傞偲
傾乮俫俠俥乯偲僀乮俫俢俥乯亖併乮侾侽俀亄侾侽俀乯亄侾侽亖俀係丏侾係們倣
僂乮俫俤俥乯亖2亊併乮侾侽俀亄俆俀乯亖俀俀丏俁俇們倣
廬偭偰摎偊偼僂偑嫍棧偑抁偔嵟弶偵摓拝偟傑偡丅
俀丏栤戣偵暻傪攪偭偰偲彂偄偰偁傝傑偟偨偑丄恾傪尒傞偲彴傕攪偭偰傛偝偦偆側偺偱
暻丄揤堜偵娭學側偔峫偊傜傟傞慡偰偺晹壆偺揥奐恾傪嶌傝寁嶼偟偰尒傑偟偨丅
嵟抁僐乕僗偼師偺僐乕僗偱偡丅
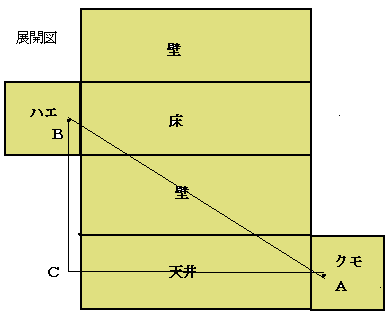
俛俠亖侾亄俁侽亄侾亖俁俀倣
俙俠亖俇亄侾俀亄俇亖俀係倣
俙俛亖併(俁俀俀亄俀係俀)亖併(侾侽俀係亄俆俈俇)亖併侾俇侽侽亖係侽倣
摎偊丂丂係侽倣

夝摎丒偦偺10
乮儁儞僱亅儉丗T_Tatekawa乯
侾丏傾偲僀偼摨偠僐乕僗傪扝偭偰偄傞丅
棫曽懱偺堦曈偺挿偝傪 1 偲偡傞偲丆傾偲僀偺挿偝偼 1+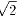
僂偺挿偝偼 併5
(1+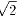 )2
= 5 + 2*
)2
= 5 + 2*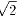 亜 5
亜 5
側偺偱丆僂偺曽偑挿偝偑抁偔丆僂傪扝偭偨傾儕偑嵟弶偵偨偳傝拝偔丏
俀丏
恾偺扝傝曽偱捠傞摴偺傝偺挿偝偼 30+12 = 42[m]
偟偐偟 1. 偺峫偊傪墳梡偡傞偲丆傕偭偲抁偄嫍棧偑偁傞帠偵婥偯偔丏
晹壆傪峔惉偡傞捈曽懱傪揥奐偟偰丆宱楬傪尒偰傒傞丏
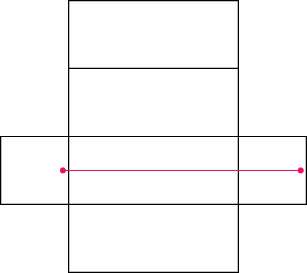 宱楬 1 偼椺偺傛偆偵偟偨傕偺偱丆42[m]
宱楬 1 偼椺偺傛偆偵偟偨傕偺偱丆42[m]
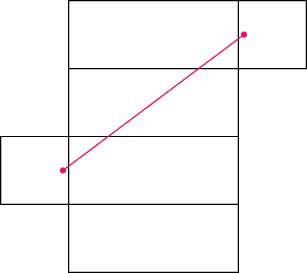 宱楬 2 偼揤堜丆懁柺丆彴傪幬傔偵扝傞傕偺偱丆挿偝偼
宱楬 2 偼揤堜丆懁柺丆彴傪幬傔偵扝傞傕偺偱丆挿偝偼
Sqrt[32*32 + 24*24] = 40 [m]
偱偡丏

夝摎丒偦偺11
乮儁儞僱亅儉丗偺偭偙傫乯
嵟抁嫍棧傪峫偊傞帪偼揥奐恾傪嶌偭偰擇揰傪捈慄偱寢傇偺偑堦斣丅
嘆揥奐恾傪嶌偭偰傒傞偲僂偑柧傜偐偵堦斣抁偄乮傾偲僀偼摨偠乯
傛偭偰懍搙偑摨偠側傜僂傪捠傞傾儕偑堦斣愭偵拝偔
嘇揥奐恾偺嶌傝曽偑栤戣丅
僴僄偺偄傞暻乮侾俀亊侾俀乯傪彴偵側傞挿曽宍乮侾俀亊俁侽乯偺嵍偵彂偒
乮彴偐傜侾m偺偲偙傠偵偄傞偐傜乯
僋儌偺偄傞暻乮侾俀亊侾俀乯傪揤堜偵側傞挿曽宍乮侾俀亊俁侽乯偺塃偵彂偗偽
乮揤堜偐傜侾m偺偲偙傠偵偄傞偐傜乯
捈妏傪偼偝傓擇曈偑俁俀倣丄俀係m偺捈妏嶰妏宍偺幬曈傪僋儌偑曕偔偙偲偵側傞丂偙傟偑嵟抁
俁俀亖俉丒係丄俀係亖俉丒俁偩偐傜偙傟偼俁丗係丗俆偺捈妏嶰妏宍
揹戩傪巊傢側偔偰傕幬曈偺挿偝偼俉丒俆亖係侽乮倣乯
仸乽暻揱偄亖彴丒揤堜傪捠傜側偄乿偲巚偄偙傫偱偟傑偄擄媀偟傑偟偨

夝摎丒偦偺12
乮儁儞僱亅儉丗岼偺柌乯
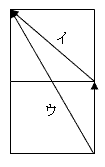
(1)棫曽懱側偺偱傾偲僀偺嫍棧偼摨偠偙偲偵側傞丅
偦偙偱棫懱恾傪揥奐偡傞偲丄塃恾偺傛偆偵側傝丄擇偮偺
捈慄偺榓偱挿偝偑嵟彫偲側傞偺偼堦捈慄偺応崌偱偁傞
偐傜僂偺傾儕偑嵟弶偵妏嵒摐偵扝傝拝偔丅
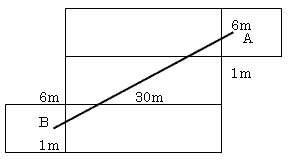
乮2乯偙傟傕揥奐恾傪昤偄偰傒傞偲丄乮1乯偲摨條偵壓恾偺
傛偆側捈慄偺応崌偵嵟抁偲側傞偙偲偑暘偐傞丅場偭偰
媮傔傞傕偺偼併322亄242亖併1600丂亖40倣偱偁傞丅

夝摎丒偦偺13
乮儁儞僱亅儉丗teki乯
乮侾乯丂僂
乮俀乯丂係侽倣
乮侾乯偼栚偱尒偰傕柧傜偐偱偡丅棫曽懱偺揥奐恾傪彂偄偰丄捈慄偵側傞儖乕僩偑嵟
抁儖乕僩偱偡偹丅
乮俀乯嵟彫偼係侽倣偪傚偆偳偱偡偹丅
捈妏傪嫴傓俀曈偺挿偝偑俀係倣偲俁俀倣偺捈妏嶰妏宍偺幬曈偺挿偝偱偡偑丄
偙傟偼丄俁丗係丗俆偺娭學傪巊偊偽丄嶰暯曽偺掕棟側偟偱寁嶼偑壜擻偱偡丅
* * * * * * * *
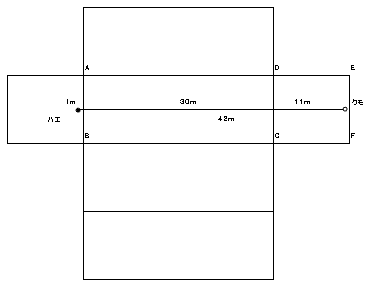
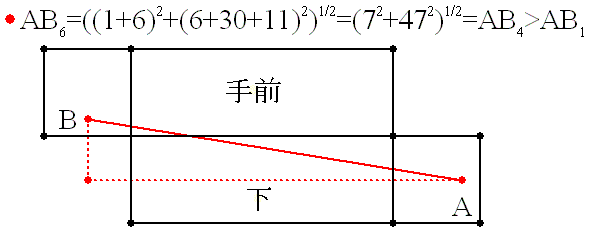
亙恾侾亜
栤戣恾偺嵟抁乮丠乯宱楬偼丄恾侾偺宱楬偱偡丅
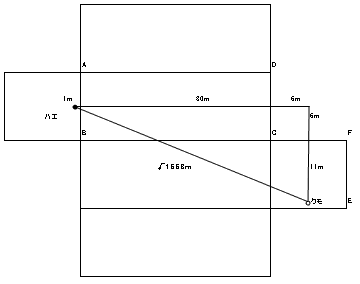
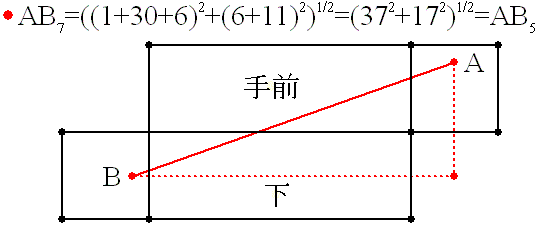
亙恾俀亜
恾俀偺宱楬偼丄巹偑嵟弶偵夝摎偟偨宱楬偱偡丅乮栤戣恾偱偄偆偲丄幬傔偵懁柺傊岦
偐偄丄偦偙偐傜幬傔偵懳柺偵岦偐偆宱楬偱偡丅乯
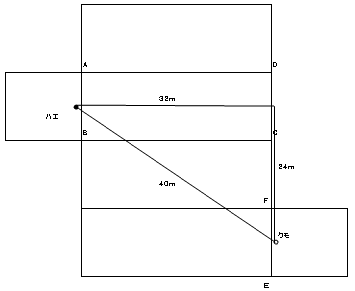
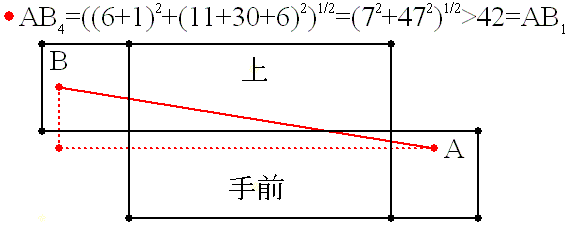
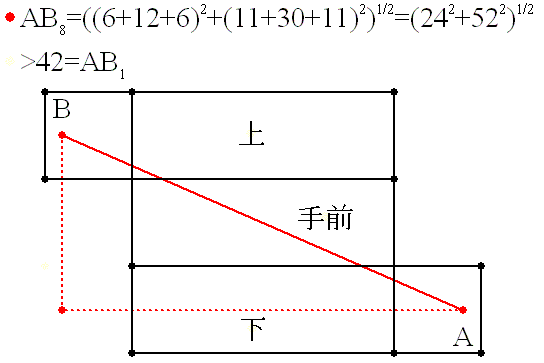
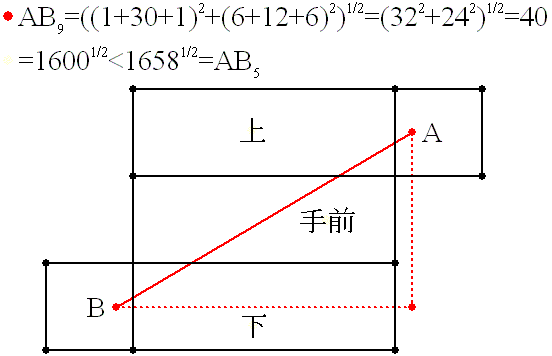
亙恾俁亜
恾俁偺宱楬偼丄傑偢丄幬傔偵揤堜偵岦偐偄丄偦偙偐傜揤堜柺丄懁柺偲宱桼偟偰栚昗
偵岦偐偆宱楬偱偡丅
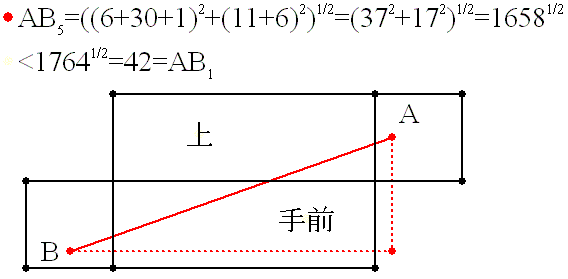
棫懱偱偼丄堦尒丄恾侾枖偼恾俀偺宱楬偑嵟抁偵尒偊傑偡偑丄幚偼恾俁偺宱楬偑墦夞
傝偟偰偄傞傛偆偱丄嵟抁宱楬偱偡偹丅
偙偺宱楬偺挿偝偼丄恾偵傕帵偟傑偟偨偑丄俀係丄俁俀丄係侽偺捈妏嶰妏宍偺幬曈偺
挿偝偱偡丅

夝摎丒偦偺14
乮儁儞僱亅儉丗Toru乯
侾丂愜傟慄偑丄堦偮偺暯柺忋偵棃傞傛偆偵棫曽懱傪揥奐偟偰峫偊傟偽丄
傾偲僀偼摨偠挿偝偱丄僂偼僀傛傝抁偄偙偲偑暘偐傞丅乮嵟抁偼曈偺拞揰傪捠傞偲偒丄
揥奐偡傞偲捈慄偵側傞乯摎偊丂僂偺傾儕
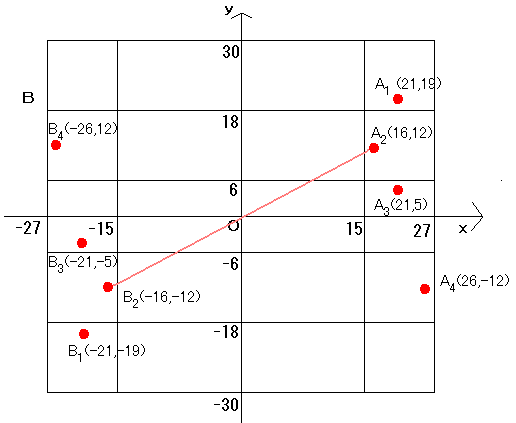
俀丂恾傪彂偐側偄乮彂偗側偄丠乯偺偱丄曗彆偲偟偰丄嵗昗傪摫擖偟偰傒傑偡丅
丂惓柺偺挿曽宍偺拞墰傪尨揰偵偟偰丄悈暯曽岦偵x幉乮-15亝x亝15乯丄屻柺偺挿曽宍
傪傑傫拞偱悈暯偵愗偭偰峀偘偰丄x幉偲悅捈偵y幉乮-24亙y 亝24乯傪庢傞丅
丂偔傕偑嵟抁僐乕僗傪庢傞応崌丄A,B傪娷傓惓曽宍偺偳傟偐偺曈傪偦傟偧傟堦搙偩偗
墶愗傞偲峫偊偰傛偄偺偱丄偦傟偧傟偵墳偠偰偦偺曈偱丄惓曽宍傪偍傝峀偘偰丄挿曽宍
偲摨堦暯柺偵傕偭偰偒偰丄偦偺晹暘偺x幉傪墑挿偡傞丅
偙傟偵傛偭偰A,B偺嵗昗偼
丂丂丂A1 (21,19) A2(16,12) A3(21,5) A4(26,-12)
丂丂丂B1(-21,-19)B2(-16,-12) B3(-21,-5) B4(-26,12)
丂AxBy偺偆偪嵟抁偺傕偺傪媮傔偰傒傞丅
懳徧惈偐傜AxBy=AyBx側偺偱丄
丂丂丂A1B1 A1B2 A1B3 A1B4 A2B2 A2B3 A2B4 A3B3 A3B4 A4B4
傪偔傜傋傟偽傛偄偑丄恾偺愒慄A4B2=A2B4=42偱丄
A1B1 A1B3 A1B4 A3B3 A3B4 A4B4丂偼柧傜偐偵偙傟傛傝挿偔丄
巆傝偺A2B2=併(322+242)=40 A1B2亜A2B3=併(372+172)=40.71---
傛傝A2B2偑嵟抁偲側傞丅
捈慄A2B2偼x=4/3 y偱偁傞偑丄偙傟偼-6亙y亙6 偱-15亝x亝15傪傒偨偡偺偱丄偙偺僐乕
僗傪庢傞偙偲偼壜擻偱丂摎偊丂40m

夝摎丒偦偺15
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
侾丏僂偺傾儕偱偡丅
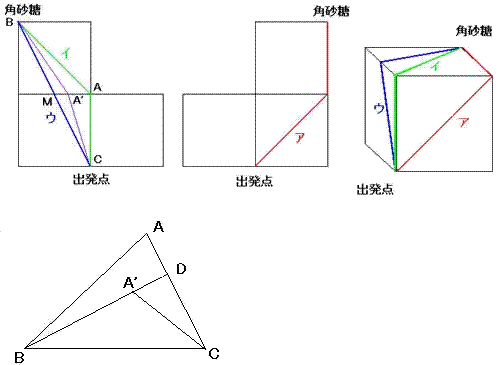
壓偺揥奐恾偱弌敪揰乮俠乯偐傜妏嵒摐乮俛乯傑偱偺嵟抁嫍棧偼捈慄偺儖乕僩偱偡丅
乮曈偺拞揰俵傪捠傞乯棫曽懱偺捀揰傪捠傜側偗傟偽丄傾傗僀偺儖乕僩傛傝偼抁偔側傝傑偡丅
嶰妏宍偺擇曈偺榓偼懠偺堦曈傛傝挿偄偙偲傪傕偪偄傞偲乽壓偺恾乿偱
丂丂丂丂俙俛亄俙俠亖俙俛亄俙俢亄俢俠
丂丂丂亜俢俛亄俢俠亖俢俙亄俙乫俛亄俢俠亖俙乫俛亄俙乫俢亄俢俠
丂丂丂亜俙乫俛亄俙乫俠
偲側傞偐傜偱偡丅
傑偨丄傾偲僀偺傾儕偼丄摨偠嫍棧傪堏摦偡傞偙偲偵側傝傑偡丅
俀丏僋儌偺嵟抁偺儖乕僩偼丄壓偺揥奐恾偺僂偺傛偆偱偡丅
摴偺傝傪俴偲偡傟偽丄
丂丂丂俴俀亖乮侾亄俁侽亄侾乯俀亄乮俇亄侾俀亄俇乯俀
丂丂丂丂丂亖俁俀俀亄俀係俀
傛傝丄係侽倣偱偡丅乮俁丗係丗俆偺捈妏嶰妏宍乯
嶲峫傑偱偵丄僀偺偲偒偼丄
丂丂丂俴俀亖乮侾亄俁侽亄俇乯俀亄乮俇亄侾侾乯俀
丂丂丂丂丂 亖俁俈俀亄侾俈俀
傛傝丄係侽丏俈侾丒丒丒倣偱偡丅
傕偪傠傫丄傾偺偲偒偼丄係俀倣偱偡丅

夝摎丒偦偺16
乮儁儞僱亅儉丗抴鍋偺憙忛乯
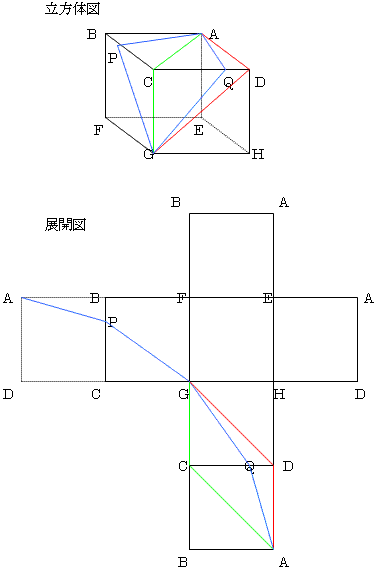
揥奐恾偵偍偄偰宱楬GCA偲GDA偼暯峴巐曈宍偺椬愙偡傞俀曈偺挿偝偺榓偱偡丅棫曽懱柺忋偺宱楬GPA偲GQA偼憡懳揑偵摨摍偱偡偐傜GQA傪嵦偭偰揥奐恾偵帵偣偽丄柧傜偐偵宱楬GQA偑堦斣懍偄偙偲偑傢偐傝傑偡丅偙偺傊傫偺婔壗妛揑棟孅偼丄偙偺嵺栚傪偮傇偭偰偟傑偄傑偟傚偆丅乮偛偪傖偛偪傖偟傑偡偐傜乯
嵟抁偺宱楬偼揰Q偑CD偺拞揰偲側傞応崌偱偡偑丄偙偺傛偆偵揥奐恾偺撪晹偱捈慄傪堷偔偙偲偑偱偒傞偲偒丄棫懱傪乽捈慄揑偵曕偔乿偲昞尰偡傞偙偲偵偟傑偟傚偆丅
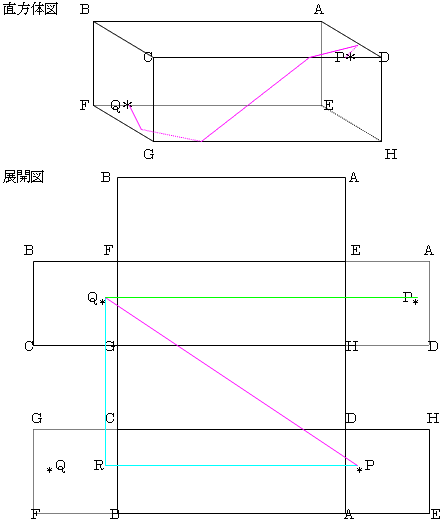
弌戣恾偵帵偝傟偨宱楬傕妋偐偵乽捈慄揑偵曕偄偰乿偄傑偡偗傟偳傕丄偦傟傛傝傕抁偄宱楬偲偟偰揥奐恾偺愒偺宱楬偑偁傝傑偡丅慄暘偑揥奐恾偺撪晹偵偁傞偙偲傪妋擣偡傞昁梫偼偁傞偱偟傚偆偑丄徣偒傑偟傚偆丅乮傔傫偳偆偱偡偐傜乯
丂丂丂PR=32丂QR=24丂傛傝嶰暯曽偱丂PQ=40丂丂椢偺宱楬丂PQ=42丂傛傝抁偄丅
偲偙傠偱丄揥奐恾偺PQ=40偑嵟抁偱偁傞偙偲偼帺柧傒偨偄側傕偺偱偡偑,埬奜偵偲偄偆偐偦傟偩偐傜偲偄偆偺偐丄榑徹偟偵偔偄偱偡偹丅乽捈慄揑偵曕偔乿宱楬偺杮悢偼桳尷偱偁傞偼偢側偺偵丄偱偡丅偱傕傑偁丄偙偺揰偵偮偄偰偼徣棯丅
偟偐偟丄棫曽懱偺応崌偵偼榑徹偟堈偄偱偡丅偙偪傜偼乽捈慄揑偵曕偔乿宱楬傪柍悢偵嶌傞偙偲偑偱偒傞偺偵丄偱偡丅偱偡偑丄偙傟傕偮偄偱偵徣棯偱偡丅

惓夝幰




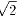 乯a
= (1+
乯a
= (1+


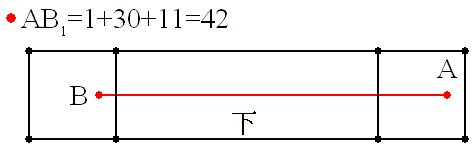

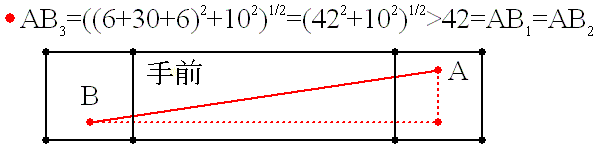











 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
 宱楬 1 偼椺偺傛偆偵偟偨傕偺偱丆42[m]
宱楬 1 偼椺偺傛偆偵偟偨傕偺偱丆42[m] 宱楬 2 偼揤堜丆懁柺丆彴傪幬傔偵扝傞傕偺偱丆挿偝偼
宱楬 2 偼揤堜丆懁柺丆彴傪幬傔偵扝傞傕偺偱丆挿偝偼









 E-mail
E-mail
 top
top