侾侽俇丏挿曽宍偺栤戣
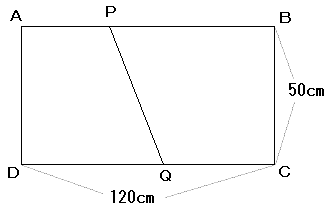
挿曽宍俙俛俠俢偑壓偺恾偺傛偆偵偁傝傑偡丅揰俹偼俙偐傜俛偺曽岦傊枅昩俀們倣丄 揰俻偼俠偐傜俢偺曽岦傊枅昩俁們倣偺懍偝偱丄偦傟偧傟偑俙丆俠傪摨帪偵弌敪偟傑偟偨丅 俹俻偑曈俙俢偲暯峴偵側傞偺偼丄弌敪偟偰偐傜壗昩屻偱偡偐丅 傑偨丄戜宍俙俹俻俢偲戜宍俛俹俻俠偺柺愊偺斾偑俆丗俈偵側傞偺偼丄弌敪偟偰偐傜壗昩屻偱偡偐丅
Weekend Mathematics乛栤戣乛106挿曽宍偺栤戣
侾侽俇丏挿曽宍偺栤戣
挿曽宍俙俛俠俢偑壓偺恾偺傛偆偵偁傝傑偡丅揰俹偼俙偐傜俛偺曽岦傊枅昩俀們倣丄 揰俻偼俠偐傜俢偺曽岦傊枅昩俁們倣偺懍偝偱丄偦傟偧傟偑俙丆俠傪摨帪偵弌敪偟傑偟偨丅 俹俻偑曈俙俢偲暯峴偵側傞偺偼丄弌敪偟偰偐傜壗昩屻偱偡偐丅 傑偨丄戜宍俙俹俻俢偲戜宍俛俹俻俠偺柺愊偺斾偑俆丗俈偵側傞偺偼丄弌敪偟偰偐傜壗昩屻偱偡偐丅

嶼悢侾侽侽偺擄栤丒婏栤
拞懞媊嶌
撳拞
島択幮僽儖乕僶僢僋僗
夝摎丒偦偺1
乮儁儞僱亅儉丗俰俽儈儖乯
曈AD偲PQ偑暯峴偵側傞偺偼丆24昩屻偱丆戜宍APQD偲 戜宍BPQC偺柺愊斾偑5丗7偵側傞偺偼20昩屻偩偲巚偄傑偡丏
夝摎丒偦偺2
乮儁儞僱亅儉丗傗側偣乯
栤侾偺摎偊偼俀係昩屻偱偡丅
曈俙俢偵暯峴偩偐傜俙俹亖俢俻偺応崌偱偡傛偹
俙俹偺挿偝偼俹揰堏摦懍搙偑俀們倣
媮傔傞帪娫傪値偲偟偨傜
俙俹亖俀値偱媮傔傜傟傑偡丅
師偵俢俻亄俠俻亖俢俠偩偐傜
俻揰堏摦懍搙偑俁們倣側偺偱俠俻亖俁値
偙傟偐傜
俢俻亖侾俀侽亅俁値丒丒偙偆偩偲巚偆偗偳
傑偀婥偵偣偢恑傔傑偟傚偆偐
忋偺忦審偐傜丠
俀値亖侾俀侽亅俁値
俀値亄俁値亖侾俀侽
値亖俀係
栤俀偺摎偊俀侽昩屻偱偡
柺愊斾偑俆丗俈傪媮傔傟偽椙偄傢偗偱偡偐傜
戜宍俙俹俻俢偺柺愊偑挿曽宍俙俛俠俢偺柺愊偺
俆乛侾俀偵側傞強傪媮傔傟偽椙偄傫偠傖側偄偐側
挿曽宍俙俛俠俢偺柺愊偼
俆侽亊侾俀侽亖俇侽侽侽偩偐傜
媮傔傞戜宍俙俹俻俢偺柺愊偼俀俆侽侽偵側傞強偱偡側
栤侾偱巊偭偨幃傪尦偵偟偰
戜宍俙俹俻俢偺柺愊偑俀俆侽侽偵側傞偵偼
偙傫側幃偱弌傞偲巚偄傑偡丅
乮俀値亄乮侾俀侽亅俁値乯乯亊俆侽亐俀亖俀俆侽侽
乮亅値亄侾俀侽乯亊俀俆亖俀俆侽侽
侾俀侽亅値亖侾侽侽
亅値亖侾侽侽亅侾俀侽
値亖俀侽
夝摎丒偦偺3
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊偼傾僀僐儞偑嫵偊偰偔傟傑偟偨両
栤戣偺夝摎傪巹偺偨傔偵俀俆昩娫峫偊偰丄摎偊嘆嘇傪15昩娫昞帵偟偰偔傟傑偟偨両
摎偊
AD偲PQ偑暯峴偵側傞帪娫偼俀係昩屻偱偡丅
柺愊偑俆丗俈偲側傞帪娫偼僗僞乕僩偟偰偐傜俀侽昩屻偱偡丅
挿曽宍俙俛俠俢偺柺愊俽亖侾俀侽亊俆侽亖俇侽侽侽
戜宍APQD偺柺愊傪俽侾丄PBCQ偺柺愊傪俽俀偲偟偰俆丗俈偲側傞帪娫傪媮傔傑偡丅
丂丂丂俽侾丗俽俀亖俆丗俈
丂丂丂俽侾亖乮俇侽侽侽乛侾俀乯仏俆亖俀俆侽侽
丂丂丂俽俀亖俇侽侽侽亅俀俆侽侽亖俁俆侽侽
俽侾偑俀俆侽侽偵側傞帪娫傪俿偲偡傞偲師偺幃偑惉傝棫偪傑偡丅
丂丂丂俆侽亊乮乮俀亊俿乯亄乮侾俀侽亅乮俁亊俿乯乯乯乛俀亖俀俆亊乮侾俀侽亅T乯亖俀俆侽侽
丂丂丂侾俀侽亖侾侽侽亄T
丂丂丂俿亖俀侽
摎偊俀侽昩屻偱偡
AD偲PQ偑暯峴偵側傞帪娫偼師偺幃偱媮傔傑偡
暯峴偵側傞帪娫傪T偲偟傑偡丅
丂丂丂T亊俀亖侾俀侽亅T亊俁
丂丂丂俆亊T亖侾俀侽
丂丂丂T=侾俀侽乛俆亖俀係
摎偊俀係昩屻偱偡
夝摎丒偦偺4
乮儁儞僱亅儉丗僯僩儘乯
侾丏宱夁偟偨帪娫傪俿昩偲偟偰丄揰俹偺埵抲傪倃噋丄揰俻偺埵抲傪倄噋傪昞偡偲丄
丂丂丂倃亖俀亊俿
丂丂丂倄亖侾俀侽亅俁亊俿
曈俙俢偵暯峴偲側傞偺偼丄倃亖倄偲側傞帪
丂丂丂亪俀俿亖侾俀侽亅俁俿
丂丂丂俆俿亖侾俀侽
丂丂丂摎偊丂俿亖俀係昩
俀丏
戜宍俙俹俻俢偺柺愊 亖乮倃亄倄乯亊俆侽乛俀 亖乮俀俿亄侾俀侽亅俁俿乯亊俆侽乛俀 亖乮侾俀侽亅俿乯亊俆侽乛俀丂丒丒丒丒丒嘆幃
戜宍俛俹俻俠偺柺愊 亖乮侾俀侽亅倃亄侾俀侽亅倄乯亊俆侽乛俀 亖乮侾俀侽亅俀俿亄侾俀侽亅侾俀侽亄俁俿乯亊俆侽乛俀 亖乮侾俀侽亄俿乯亊俆侽乛俀丂丒丒丒丒丒嘇幃
柺愊斾偑俆丗俈側偺偱
丂丂丂俆丗俈亖嘆幃丗嘇幃亖乮侾俀侽亅俿乯亊俆侽乛俀丗乮侾俀侽亄俿乯亊俆侽乛俀
丂丂丂俆亊乮侾俀侽亄俿乯亖俈亊乮侾俀侽亅俿乯
丂丂丂俇侽侽亄俆俿亖俉係侽亅俈俿
丂丂丂侾俀俿亖俀係侽
丂丂丂摎偊丂俿亖俀侽昩
俀丏亙暿夝亜戜宍俙俹俻俢偺柺愊偑俀俆侽侽噋俀偺帪丄柺愊斾偑俆丗俈偲側傞偺偱
丂丂丂嘆幃亖乮侾俀侽亅俿乯亊俆侽乛俀亖俀俆侽侽
丂丂丂侾俀侽亅俿亖侾侽侽
丂丂丂俿亖俀侽昩
夝摎丒偦偺5
乮儁儞僱亅儉丗Ozk乯
AP=x丂, CQ=y偲偡傞偲丄揰俹偼俙偐傜俛偺曽岦傊枅昩俀們倣丄揰俻偼俠偐傜俢偺曽岦 傊枅昩俁們倣偺懍偝偱恑傓偺偱丄2揰P,Q偑揰A,C傪弌敪偟偰偐傜t昩屻偺x,y偺挿偝偼 x=2t丄y=3t偲昞偣傞丅
乮侾乯
俹俻偑曈俙俢偲暯峴偵側傞帪崗傪t偲偡傞丅 PQ//AQ偲側傞偲偒丄AP=DQ偱偁傞丅
丂丂丂DQ=DC-QC=120-y丂傑偨丂AP=x
傛偭偰丄120-y=x偑惉傝棫偪丄x=2t丄y=3t傪戙擖偟偰
丂丂丂120-3t=2t
偙傟傪夝偄偰丂t=24
傛偭偰弌敪偟偰偐傜24昩屻偵俹俻偑曈俙俢偲暯峴偵側傞
乮俀乯
戜宍俙俹俻俢偲戜宍俛俹俻俠偺柺愊傪偦傟偧傟S1丄S2偲偍偔丅
丂丂丂S1=(AP+DQ)*AD/2 = (x+120-y)*AD/2
丂丂丂S2=(PB+QC)*BC/2 = (120-x+y)*BC/2
偙偙偱丄AP=BC=50cm側偺偱
丂丂丂S1:S2亖(x+120-y)*AD/2:(120-x+y)*BC/2 =(x+120-y):(120-x+y)=5:7
備偊偵
丂丂丂5(120-x+y)=7(x+120-y)
偙偺幃偵x=2t丄y=3t傪戙擖偟偰
丂丂丂5(120-2t+3t)=7(2t+120-3t)
偙傟傪夝偄偰 t=20
傛偭偰弌敪偟偰偐傜俀侽昩屻偵戜宍俙俹俻俢偲戜宍俛俹俻俠偺柺愊偺斾偑俆丗俈偵側傞
夝摎丒偦偺6
乮儁儞僱亅儉丗偪偐傂偱乯
俢傪尨揰偲偡傞捈岎嵗昗傪峫偊傞丅
侾丏倲昩屻偺揰俹偺倶嵗昗丗倶1亖2倲
丂丂丂丂丂丂揰俻偺倶嵗昗丗倶2亖120-3倲
丂丂俹俻偑曈俙俢偲暯峴偵側傞偲偒倶1亖倶2
丂丂丂丂亪2倲亖120-3倲
丂丂丂丂丂倲亖120乛5亖24乮倱乯
俀丏俙俹俻俢偺柺愊俙1丆俛俹俻俠偺柺愊俙2偲偡傞丅
丂丂丂丂俙1亖{2倲亄乮120-3倲乯}亊50乛2
丂丂丂丂俙2亖{乮120-2倲乯亄3倲}亊50乛2
丂丂丂丂5乛7亖俙1乛俙2亖{2倲亄乮120-3倲乯}乛{乮120-2倲乯亄3倲}
丂丂丂丂丂丂丂丂丂丂丂亖乮120-倲乯乛乮120亄倲乯
丂丂丂亪5{120亄倲乯亖7乮120-倲乯
丂丂丂丂600亄5倲亖840-7倲
丂丂丂丂倲亖240乛12亖20乮倱乯
俙値倱丏俹俻偑曈俙俢偲暯峵偵側傞偺偼俀係昩屻丅
戜宍俙俹俻俢偲戜宍俛俹俻俠偺柺愊偺斾偑俆丗俈偵側傞偺偼俀侽昩屻丅
夝摎丒偦偺7
乮儁儞僱亅儉丗mhayashi乯
t 昩屻偵 PQ 偑 AD 偲暯峴偵側偭偨偲偡傞丏
偮傑傝 AP=DQ 偺忬懺偱偁傝
2t=120-3t 偑惉傝棫偮丏
傛偭偰 t=24 傛傝丆PQ 偑 AD 偲暯峴偵側傞偺偼 24 昩屻丏
u 昩屻偵戜宍APQD偲戜宍BPQC偺柺愊斾偑 5:7 偵側偭偨偲偡傞丏
戜宍APQD=(2u+120-3u)*50/2=25(120-u)
戜宍BPQC=(120-2u+3u)*50/2=25(120+u)
偙傟傜傛傝 (120-u):(120+u)=5:7 傪夝偄偰 u=20
傛偭偰戜宍APQD偲戜宍BPQC偺柺愊斾偑 5:7 偵側傞偺偼 20 昩屻
夝摎丒偦偺8
乮儁儞僱亅儉丗T_Tatekawa乯
揰 P, Q 偑恑傫偩嫍棧偺崌寁偑 120cm 偵側傞帪偑丆PQ 偑 曈 AD 偲 暯峴偵側傞帪側偺偱丆
丂丂丂120 / (3+2) = 24 昩屻
戜宍 APQD 偲 戜宍 BPQC 偺柺愊偺斾偑 5:7 偵側偭偨帪丆奺乆偺柺愊偼
丂丂丂APQD: 50*120 * 5/(5+7) = 2500 cm2
丂丂丂BPQC: 50*120 * 7/(5+7) = 3500 cm2
嵟弶偼偙傟傜偺戜宍偺柺愊偼
丂丂丂50 * 120 / 2 = 3000 cm2
偱偁傞丏1昩偛偲偵戜宍 BPQC 偺柺愊偼
丂丂丂(3-2) * 50 /2 = 25 cm2
偢偮憹壛偡傞偺偱丆柺愊偺斾偑 5:7 偵側傞偺偼丆
丂丂丂(3500-3000) / 25 = 20 昩屻
夝摎丒偦偺9
乮儁儞僱亅儉丗帥榚將乯
暯峴偵側傞傑偱偺昩悢傪丂倶丂偲偡傞偲
丂丂丂俙俹亖俀倶丂丂丂丂俠俻亖俁倶
恾偺俹偐傜丂俢俠偵壓傠偟偨悅慄偺懌傪丂俵丄 俻偐傜丂俙俛偵壓偟偨悅慄偺懌傪丂俶偲偡傞丅 俹俻偑俙俢偲暯峴偵側傞偲偼
丂丂丂俹俻亖俹俵丄俹俻亖俻俶
偵側傞偙偲丅偙傟偼丂挿曽宍俹俵俻俶傪峫偊偰丄 俹俵偲俻俶偑廳側傞偲丂懳妏慄俹俻偼俹俵丄俻俶偲堦抳偡傞丅 偲偡傞偲
丂丂丂俀x + 俁x = 侾俀侽
偑尵偊偰丂丂偙傟傪夝偄偰丄倶亖俀係
丂丂丂摎偊丂俀係昩屻
師偵丂柺愊斾偑丂俆丟俈丂偵側傞傑偱偺昩悢傪丂倷偲偡傞偲
丂丂丂AP亖俀y CQ亖俁倷
偱挿曽宍俙俢俠俛偺柺愊傪丂俆丗俈丂偵暘偗傞偲
丂丂丂戜宍俙俢俻俹亖俀俆侽侽
丂丂丂戜宍俹俻俠俛亖俁俆侽侽
偦傟偐傜丂挿曽宍俹俵俻俶傪丂懳妏慄俹俻偱暘偗傞偲
丂丂丂嶰妏宍俹俵俻丂亖丂嶰妏宍俻俶俹
偦偟偰丂挿曽宍俙俢俵俹亖侾侽侽倷
丂丂丂丂挿曽宍俶俻俠俛亖侾俆侽倷
埲忋傛傝
丂丂丂戜宍俙俢俻俹丂乕丂挿曽宍俙俢俵俹亖丂嶰妏宍俹俵俻
丂丂丂戜宍俹俻俠俛丂乕丂挿曽宍俶俻俠俛亖丂嶰妏宍俻俶俹
偙傟傛傝
俀俆侽侽乕侾侽侽倷丂亖俁俆侽侽亅侾俆侽倷
丂丂丂丂丂丂丂倷亖丂俀侽
摎偊丂俀侽昩屻
夝摎丒偦偺10
乮儁儞僱亅儉丗昹揷丂柧枻乯
倶昩屻偵俙俢//俹俻偲側傞偲偡傞丏
丂俙俹亖俢俻偲側傟偽傛偄偐傜丆
丂丂俀倶亖侾俀侽亅俁倶
丂丂亪俆倶亖侾俀侽
丂丂亪倶亖俀係
丂屘偵俀係昩屻偱偁傞丏
丂師偵倶昩屻偵戜宍俙俹俻俢丗戜宍俛俹俻俠亖俆丗俈偵側傞偲偡傞丏
丂戜宍俙俹俻俢亄戜宍俛俹俻俠亖挿曽宍俙俢俠俛側偺偱丆
丂丂戜宍俙俹俻俢亖俆乛(俆亄俈)亊挿曽宍俙俢俠俛
丂丂亪{俀倶亄(侾俀侽亅俁倶)}亊俆侽乛俀亖俆乛侾俀亊俆侽亊侾俀侽
丂丂亪侾俀侽亅倶亖侾侽侽
丂丂亪倶亖俀侽
丂屘偵俀侽昩屻偱偁傞丏
傑偨恾宍偺栤戣側偺偱丆Visual Basic偱傕夝偄偰傒偨丏傗偼傝摨偠寢壥偲側偭偨丏
Option Explicit Sub Form_Load() Dim waku As Double waku = 5 Picture1.Scale (-waku, 85 + waku)-(120 + waku, -35 - waku) Picture1.BackColor = vbWhite Picture2.BackColor = vbWhite Picture2.Picture = LoadPicture("mondai106a.gif") Picture3.BackColor = vbWhite End Sub Sub Command1_Click() Call keisan(1) End Sub Sub Command3_Click() Call keisan(2) End Sub Sub keisan(ByVal mondai As Integer) Dim Ax As Double Dim Ay As Double Dim Bx As Double Dim By As Double Dim Cx As Double Dim Cy As Double Dim Dx As Double Dim Dy As Double Dim Px As Double Dim Py As Double Dim Qx As Double Dim Qy As Double Dim Pxx As Double Dim Qxx As Double Dim t As Double Dim tt As Double Dim t_min As Double Dim t_max As Double Dim t_min0 As Double Dim t_max0 As Double Dim kizami As Double Dim sa As Double Dim min As Double Dim dankai As Integer Dim dankai_max As Integer ' Ax = 0 Ay = 50 Bx = 120 By = 50 Cx = 120 Cy = 0 Dx = 0 Dy = 0 Py = 50 Qy = 0 t_min0 = 0 t_max0 = 120 / 3 kizami = 0.1 min = 1000000 dankai_max = 14 For dankai = 1 To dankai_max + 1 If dankai = 1 Then t_min = t_min0 t_max = t_max0 ElseIf dankai <= dankai_max Then t_min = max2(tt - kizami, t_min0) t_max = min2(tt + kizami, t_max0) kizami = kizami * 0.1 Else t_min = tt t_max = tt End If For t = t_min To t_max Step kizami If dankai <= dankai_max Then Px = 2 * t Qx = 120 - 3 * t If mondai = 1 Then sa = Abs(Px - Qx) Else sa = Abs((0.5 * (Px + Qx) * Ay) / (0.5 * ((Bx - Px) + (Cx - Qx)) * Ay) - 5 / 7) End If If min > sa Then min = sa tt = t Pxx = Px Qxx = Qx Picture3.Cls If mondai = 1 Then Picture3.Print tt; "昩屻(?), 乥AP-DQ乥="; min Else Picture3.Print tt; "昩屻(?), 乥戜宍APQD/戜宍BPQC-5/7乥="; min End If End If Picture1.Cls Picture1.Line (Pxx, Py)-(Qxx, Qy), vbGreen Else Px = Pxx Qx = Qxx Picture3.Cls If mondai = 1 Then Picture3.Print tt; "昩屻, 乥AP-DQ乥="; min Else Picture3.Print tt; "昩屻, 乥戜宍APQD/戜宍BPQC-5/7乥="; min End If Picture1.Cls End If Picture1.Line (Ax, Ay)-(Bx, By), vbBlack Picture1.Line -(Cx, Cy), vbBlack Picture1.Line -(Dx, Dy), vbBlack Picture1.Line -(Ax, Ay), vbBlack Picture1.Line (Px, Py)-(Qx, Qy), vbBlack Picture1.CurrentX = Ax Picture1.CurrentY = Ay Picture1.Print "A" Picture1.CurrentX = Bx Picture1.CurrentY = By Picture1.Print "B" Picture1.CurrentX = Cx Picture1.CurrentY = Cy Picture1.Print "C" Picture1.CurrentX = Dx Picture1.CurrentY = Dy Picture1.Print "D" Picture1.CurrentX = Px Picture1.CurrentY = Py Picture1.Print "P" Picture1.CurrentX = Qx Picture1.CurrentY = Qy Picture1.Print "Q" Next t Next dankai End Sub Sub Command2_Click() Unload Me End Sub Private Function min2(ByVal x As Double, ByVal y As Double) As Double If x < y Then min2 = x Else min2 = y End If End Function Private Function max2(ByVal x As Double, ByVal y As Double) As Double If x > y Then max2 = x Else max2 = y End If End Function
夝摎丒偦偺11
乮儁儞僱亅儉丗夝摎儖僷儞乯
(1)曈AB偲PQ偑暯峴偵側傞偵偼丄AP偺挿偝偲DQ偺挿偝偑摍偟偔側傞偲偒偱偡偺偱丄 P偺懍搙偼2cm/sec丂Q偺懍搙偼3cm/sec丂偱偡偺偱丄宱夁帪娫t[sec]偲偍偔偲
丂丂丂AP=2丒t
丂丂丂DQ=120亅3丒t
丂丂丂AP=DQ
偲側傞偺偱丄偙傟傪夝偔偲
丂丂丂2丒t=120亅3丒t
丂丂丂亪t=24sec丂
傛偭偰24昩屻偱偡丅
(2)戜宍俙俹俻俢偲戜宍俛俹俻俠偺柺愊偺斾偑俆丗俈偲側傞偲偒偼 戜宍偺崅偝偑摍偟偄偺偱丂乮忋掙亄壓掙乯偺斾偑俆丗俈偲側傞帪娫傪媮傔傟偽傛偄偺偱丄
丂丂丂PB亖120亅2丒t
丂丂丂QC亖3丒t
戣堄傛傝乮AP+DQ乯:乮PB亄QC乯亖俆丗俈丂偱偡偐傜
丂丂丂乮2丒t亄120-3丒t乯丗乮120亅2丒t亄3丒t乯亖俆丗俈
丂丂丂7丒乮t亅120乯亖5丒乮120亄t乯
丂丂丂亪倲亖20sec
傛偭偰20昩屻偱偡丅
夝摎丒偦偺12
乮儁儞僱亅儉丗崅峑嫵堳巙朷偺拞妛峑悢妛嫵堳乯
(1)丂俹俻偑曈俙俢偲暯峴偵側傞応崌
x昩屻偵暯峴偵側傞偲偡傞偲丄
丂丂丂AP=2x丂丂丂丒丒丒嘆
丂丂丂CQ=3x丂
丂丂丂DQ=CD-CQ=120-3x丂丒丒丒嘇
暯峴偵側傞偲偒偼AP=DQ側偺偱丄 嘆嘇傛傝
丂丂丂2x=120-3x
丂丂丂5x=120
丂丂丂x=24
傛偭偰丄24昩屻偵暯峴偵側傞両両
(2)丂戜宍俙俹俻俢偲戜宍俛俹俻俠偺柺愊偺斾偑俆丗俈偵側傞 応崌
偙偺応崌偑y昩屻偲偡傞偲丄
戜宍APQD偺柺愊傪Sa丄戜宍BPQC偺柺愊傪Sb偲偡傞偲丄俆丗俈側偺偱丄
丂丂丂5Sb丂丂丂 亖丂7Sa
丂丂丂5(CQ+BP) 亖丂7(AP+DQ)
丂丂丂5(3y+120-2y) 亖丂7(2x+120-3x)
丂丂丂12y 亖 240
丂丂丂y 亖 20
傛偭偰丄20昩屻偵丄戜宍俙俹俻俢偲戜宍俛俹俻俠偺柺愊偺斾偑 俆丗俈偵側傞
夝摎丒偦偺13
乮儁儞僱亅儉丗偺偭偙傫乯
嘆暯峴
t昩屻偺AP亖俀t丄DQ亖侾俀侽亅俁t
摍偟偄偲偍偄偰丂t亖俀係
嘇俆丗俈
t昩屻偺AP亖俀t丄DQ亖侾俀侽乕俁t
丂丂丂AP亄DQ亖侾俀侽亅t
t昩屻偺PB亖侾俀侽亅俀t丄QC亖俁t
丂丂丂PB亄QC亖侾俀侽亄t
乮侾俀侽亅t乯丗(120亄t乯亖俆丗俈偲偍偄偰t亖俀侽
俆侽cm偲偄偆偺偼晄梫偱偡偹
夝摎丒偦偺14
乮儁儞僱亅儉丗岼偺柌乯
(1)暯峴偲側傞弌敪屻偺昩悢傪丂倲丂偲偡傞偲丄 戣堄傛傝丂2倲丂亖丂120-3倲丂偑惉棫偡傞丅偙傟傛傝媮傔傞丂倲丂偼24昩屻偱偁傞丅
乮2乯椉曽偲傕戜宍偱偁傝丄崅偝偼摍偟偄丅場偭偰柺愊斾偼忋掙偲壓掙偺榓偵斾椺偡傞偺偱丄 (3倲亄120-2倲)丂/丂乮2倲亄120-3倲乯丂亖丂7/5丂偑惉棫偡傞丅偙傟傪夝偄偰丂倲亖丂20偲側傞丅 場偭偰媮傔傞傕偺偼丂20昩屻偱偁傞丅
夝摎丒偦偺15
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
揰俹偲俻偑弌敪偟偰偐傜宱夁偟偨帪娫傪倲 昩偲偟傑偡丅
俹俻偑曈俙俢偲暯峴偵側傞偺偼丄俙俹偺挿偝偲俢俻偺挿偝偑摍偟偄偲偒側偺偱丄
丂丂丂俀倲亖侾俀侽亅俁倲
亪丂倲亖俀係 屻偱偡丅乮愒偺恾乯
傑偨丄戜宍俙俹俻俢偲戜宍俛俹俻俠偺柺愊偺斾偑俆丗俈偵側傞偺偼丄
戜宍俙俹俻俢丗戜宍俛俹俻俠 亖 乮俀倲亄侾俀侽亅俁倲乯亊俆侽亐俀丗乮侾俀侽亅俀倲亄俁倲乯亊俆侽亐俀 亖 乮侾俀侽亅倲乯丗乮侾俀侽亄倲乯亖俆丗俈
側偺偱丄
倲亖俀侽 昩屻偱偡丅乮椢偺恾乯
夝摎丒偦偺16
乮儁儞僱亅儉丗僪儞僉乕乯
揰俻偑嵟弶偵揰俢偵摓払偟偨偁偲偺揰偺摦偒曽偑彂偄偰偄側偄偺偱丄偦偺帪揰傑偱偱峫偊傞偙偲偵偟傑偡丅 揰俹丆俻偑弌敪偟偨帪崗傪侽偲偟丄偦偙偐傜倲昩屻偺忬懺傪峫偊傞偲丄俙俹亖2倲乮們倣乯丆俻俠亖3倲乮們倣乯偱偡丅
俹俻偲俙俢偑暯峴偵側傞偲偒丄俹俛亖俻俠側偺偱
丂丂丂俙俹+俻俠亖俙俹+俹俛亖俙俛亖120乮們倣乯
傛偭偰丂丂2倲+3倲亖120丂丂丂亪倲亖24乮昩屻乯丂丒丒丒乮摎乯
師偵戜宍偵偮偄偰峫偊傑偡丅
戜宍偺柺愊偼丂乮忋掙+壓掙乯亊崅偝亐俀丂偱媮傔傜傟傑偡偑丄 崱丄戜宍俙俹俻俢偲戜宍俛俹俻俠偼崅偝偑50乮們倣乯偱嫟捠側偺偱丄 柺愊斾偼乮忋掙+壓掙乯偺斾偲摨偠偵側傝傑偡丅 傛偭偰偦偺柺愊斾偑俆丗俈偺偲偒丄
丂丂丂乮俙俹+俢俻乯丗乮俹俛+俻俠乯亖俆丗俈
丂丂丂乷2倲+乮120-3倲乯乸丗乷乮120-2倲乯+3倲乸亖俆丗俈
丂丂丂7乮120-倲乯亖5乮120+倲乯
亪倲亖20乮昩屻乯丂丒丒丒乮摎乯
乮柺愊斾偵偮偄偰暿夝乯
傑偢丄仮俙俢俠亖仮俛俙俠亖3000乮們倣2乯偱偡丅 揰俹丆俻偑弌敪偡傞慜偼丄戜宍俙俹俻俢亖仮俙俢俠丄戜宍俛俹俻俠亖仮俛俙俠偲尒傞偙偲偑弌棃傞偺偱丄 柺愊斾偼侾丗侾偱偡丅偑丄偙偙偱偼俇丗俇偲偲傜偊傞偙偲偵偟傑偟傚偆丅
偝偰丄揰俹丆俻偑弌敪偟傑偡丅 偙偺偲偒丄傕偟揰俻偑巭傑偭偰偄傟偽丄戜宍俙俹俻俢偺柺愊偼仮俙俹俠偺暘偩偗丄偮傑傝50倲乮們倣2乯偩偗憹偊傑偡丅 傑偨丄傕偟揰俹偑巭傑偭偰偄傟偽丄戜宍俙俷俻俢偺柺愊偼仮俠俙俻偺暘偩偗丄偮傑傝75倲乮們倣2乯偩偗尭傝傑偡丅 偟偨偑偭偰揰俹丆俻偲傕偵摦偔偲丄戜宍俙俹俻俢偺柺愊偼丂75倲亅50倲亖25倲乮們倣2乯丂偩偗尭傝傑偡丅 偙偺尭傝暘偼丄戜宍俛俹俻俠偺柺愊偺憹暘偲摨偠偱偡丅 嵟弶丄擇偮偺戜宍偼柺愊斾俇丗俇偩偭偨傢偗偱偡偐傜丄 俆丗俈偵側傞偲偒丄戜宍俙俹俻俢偑俇偺偆偪侾偺暘偩偗戜宍俛俹俻俠偵偁偘偨偙偲偵側傝傑偡丅 偮傑傝丄戜宍俙俹俻俢偺尭傝暘偺25倲偑丄嵟弶偺3000乮們倣2乯偺1/6偵側傞傢偗偱偡丅 傛偭偰丂25倲亖3000亊1/6丂丂亪倲亖20乮昩屻乯
夝摎丒偦偺17
乮儁儞僱亅儉丗Toru乯
x昩屻丂AP=2x cm DQ=(120-3x) cm
1)PQ偑AD偲暯峴偵側傞偺偼AP=DQ偺帪偱丄2x=120-3x 傛傝x=24 昩屻
2)戜宍APQD丗戜宍PBCQ=(AP+DQ)丗(PB+QC)=(120-x)丗(120+x)=5丗7
傛傝 x=20 昩屻
彫妛惗偑夝偔偺偩偐傜丄X傪巊偭偰偼偄偗側偄偲偡傞偲丄
1) 120cm 偺摴偺傝傪枅昩2cm+3cm=5cm偱嬤偯偄偰丄弌夛偭偨帪偵暯峴偩偐傜丄 120/5=24 昩
2)戜宍偺柺愊偺岞幃傪巊偭偰偄偄偺偐偳偆偐暘偐傝傑偣傫偑丄偙傟傕偩傔側傜丄 戜宍ADQP傪儮ADQ偲儮QAP偲偵暘妱偡傞側偳偟偰丄戜宍偺柺愊斾偼(AP+DQ)丗(PB+QC)丄 偙偺榓偼AB+DC=240cm側偺偱丄偙傟傪5丗7偵暘偗傞偲240x5/12=100傛傝100cm 偲140cm 丄 (AP+DQ)偼120cm偐傜枅昩2cm-3cm=-1cm 傛傝1cm尭傞偐傜丄 100cm偵側傞傑偱偺帪娫偼20昩
夝摎丒偦偺18
乮儁儞僱亅儉丗nao乯
俹俻偑俙俢偲暯峴偵側傞偺偼丄俙俹偲俠俻偺榓偑侾俀侽們倣偵側偭偨偲偒偱偡丅
俙俹偼堦昩偱俀們倣丄俠俻偼堦昩偱俁們倣恑傓偺偱丄
侾俀侽亐乮俀亄俁乯亖俀係丂丂丂摎偊丂俀係昩屻
偮偓偵丄戜宍俙俹俻俢偲戜宍俛俹俻俠偼丄崅偝偑摨偠側偺偱丄柺愊偺斾偼忋掙偲壓掙 偺榓偺斾偵側傝傑偡丅
傑偨丄俙俹亄俻俢偲俛俹亄俻俠偺榓偼偮偹偵俀係侽們倣偱偡丅
柺愊斾偑俆丗俈偵側傞偲偄偆偙偲偼丄俙俹亄俻俢偑
俀係侽亊俆乛乮俆亄俈乯亖侾侽侽們倣
俛俹亄俻俠偑
係侽亊俈乛乮俆亄俈乯亖侾係侽們倣
偺偲偒偱偡丅
俙俹亄俻俢偼丄俙俹偑堦昩娫偵俀們倣傆偊丄俻俢偑堦昩娫偵俁們倣偯偮尭偭偰偄偔偺 偱丄崌寁偱堦昩娫偵侾們倣偯偮尭偭偰偄偒傑偡丅
嵟弶偑侾俀侽們倣側偺偱丄侾侽侽們倣偵側傞偺偼丄 侾俀侽乕侾侽侽亖俀侽昩屻偵側傝傑偡丅
妋擣偺偨傔偵丄俛俹亄俻俠偱傕峫偊傞偲丄俛俹偼堦昩娫偵俀們倣偯偮尭傝丄俻俠偼堦 昩娫偵俁們倣偯偮憹偊傞偺偱丄崌寁偱侾僙儞僠偯偮憹偊傑偡丅
嵟弶偑偙傟傕侾俀侽們倣側偺偱丄侾係侽們倣偵側傞偺偼丄 侾係侽乕侾俀侽亖俀侽昩屻丂偱偁偭偰偄傑偡丅
摎偊丂俀侽昩屻
夝摎丒偦偺19
乮儁儞僱亅儉丗teki乯
侾丂俀係昩屻
俀丂俀侽昩屻
椉曽偲傕曽掱幃偱夝偗傑偡偹丅
侾偼丄倶昩屻偺俙俹偲俢俻偺挿偝偑摍偟偗傟偽偄偄偺偱丄俀倶亖侾俀侽亅俁倶丂傪夝 偄偰
倶亖俀係
俀偼丄戜宍俙俹俻俢偺柺愊偑俀俆侽侽們倣俀偵側傟偽偄偄偺偱丄
乮俀倶亄侾俀侽亅俁倶乯亊俀俆亖俀俆侽侽
仺丂乮侾俀侽亅倶乯亖侾侽侽丂偱丂倶亖俀侽
崱寧偺栤戣偺嶼悢揑側夝朄傪峫偊偰傒傑偟偨丅 偱丄偱偒偨偺偑丄埲壓偺栤戣偱偡丅
栤戣
挿偝侾俀侽們倣偺慄暘AB偑偁傞丅 揰P偼A偐傜枅昩俀們倣偱B偵岦偐偄丄揰Q偼B偐傜枅昩俁們倣偱A偵岦偐偭偰摨帪偵恑 傓丅 偙偺帪丄師偺栤偄偵摎偊側偝偄丅
乮侾乯丂揰P偲揰Q偑弌夛偆偺偼丄弌敪偟偰偐傜壗昩屻偐丅
乮俀乯丂慄暘PQ偺拞揰傪M偲偡傞丅
丂丂丂揰M偑慄暘AB傪俆丗俈偵撪暘偡傞偺偼丄弌敪偟偰偐傜壗昩屻偐丅
夝摎
乮侾乯丂侾俀侽們倣偺嫍棧傪枅昩俀們倣偲俁們倣偺揰偑屳偄偵岦偐偄崌偭偰恑傓偺偱偡偐 傜丄弌夛偆偺偼丄侾俀侽亐乮俀亄俁乯亖俀係昩屻丅
乮俀乯丂俀偮偺揰偺拞揰M偼丄枅昩乮俁亅俀乯亐俀亖侽丏俆們倣偢偮嵍乮A懁乯偵堏摦偟傑 偡丅偙傟偑丄慄暘AB傪俆丗俈偵撪暘偡傞偺偼丄拞墰偐傜侾侽們倣嵍偵堏摦偟偨帪偱 偡丅傛偭偰丄侾侽亐侽丏俆亖俀侽昩屻丅
惓夝幰
teki 岼偺柌 nao 僪儞僉乕 T_Tatekawa 傗側偣 昹揷丂柧枻 俰俽儈儖 Toru Ozk 偺偭偙傫 栭傆偐偟偺偮傜偄偍偠偝傫 崅峑嫵堳巙朷偺拞妛峑悢妛嫵堳 僯僩儘 忨偺偍偠偝傫 夝摎儖僷儞 偪偐傂偱 帥榚將 mhayashi
偙偺栤戣偼丄帪崗傪曄悢倲偲偍偄偰丄曽掱幃傪棫偰偰夝偔偲偄偆偺偑掕愇偩偲巚偄傑偡偑丄 偁偊偰曽掱幃傪梡偄偢偵傾僾儘乕僠偟偰傒傞偺傕偍傕偟傠偄偲巚偄傑偡丅 壗恖偐偺曽偐傜丄偦偆偄偭偨夝摎傪婑偣偰偄偨偩偒傑偟偨丅偳偆傕偁傝偑偲偆偛偞偄傑偡丅
傑偨丄偺偭偙傫偝傫偑偛巜揈偟偰偔偩偝偭偰偄傞傛偆偵丄 偙偺栤戣傪夝偔嵺偵丄挿曽宍偺崅偝50cm偲偄偆偺偼娭學偟傑偣傫偹丅 挿曽宍傪戣嵽偵偟偰偄傑偡偑丄幚偼慄暘忋偺栤戣偱偁傞傢偗偱偡丅 偦傟傪丄teki偝傫偑抂揑偵昞尰偟偰偔偩偝偄傑偟偨丅

 E-mail
E-mail
 top
top