103.折り紙の問題
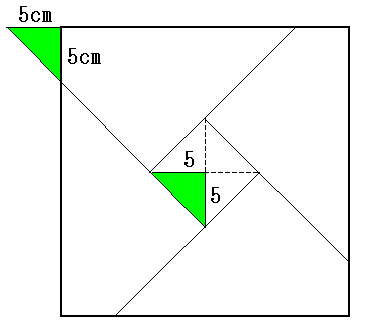
右の図のように、正方形の折り紙を5つの部分に切りました。折り紙の4すみから5cmのところで、45°にハサミを入れ、中央に小さな正方形ができるようにしたものです。この小さな正方形の面積は何cm2ですか。
Weekend Mathematics/問題/問題103
103.折り紙の問題
右の図のように、正方形の折り紙を5つの部分に切りました。折り紙の4すみから5cmのところで、45°にハサミを入れ、中央に小さな正方形ができるようにしたものです。この小さな正方形の面積は何cm2ですか。
算数100の難問・奇問
中村義作
高田中
講談社ブルーバックス
解答・その1
(ペンネ-ム:浜田 明巳)
図形の問題なので,VISUAL BASICで解いた.答は一定値の50cm2である.プログラムは中の小さな正方形が一定の大きさを保っている様子が分かるようになっている.
(コピー&貼り付けする際は,全角の空白を半角にしなくてはなりません)
Option Explicit Const MAX As Double = 100 '******** Const KIZAMI As Double = 0.01 '******** Sub Form_Load() Dim waku As Double waku = MAX * 0.1 Picture1.Scale (-waku, MAX + waku)-(MAX + waku, -waku) Picture1.BackColor = vbWhite Picture2.BackColor = vbWhite Picture2.Picture = LoadPicture("gazou103a.gif") Picture3.BackColor = vbWhite Picture4.BackColor = vbWhite End Sub Sub Command1_Click() Dim Ax As Double Dim Ay As Double Dim Bx As Double Dim By As Double Dim Cx As Double Dim Cy As Double Dim Dx As Double Dim Dy As Double Dim Ex As Double Dim Ey As Double Dim Fx As Double Dim Fy As Double Dim Gx As Double Dim Gy As Double Dim Hx As Double Dim Hy As Double Dim Ix As Double Dim Iy As Double Dim Jx As Double Dim Jy As Double Dim Kx As Double Dim Ky As Double Dim Lx As Double Dim Ly As Double Dim Ay_max As Double Dim Ay_min As Double Dim a As Double Dim b As Double Dim c As Double Dim d As Double Dim menseki As Double Dim wa As Double Dim wa2 As Double Dim heikin As Double Dim kaisuu As Long Dim hyoujunhensa As Double ' Ax = 0 Bx = 0 By = 0 Cy = 0 Ex = 0 Fx = 5 Fy = 0 Gy = 5 Ay_max = MAX Ay_min = 5 + KIZAMI wa = 0 wa2 = 0 kaisuu = 0 For Ay = Ay_min To Ay_max Step KIZAMI Cx = Ay Dx = Ay Dy = Ay Ey = Ay - 5 Gx = Ay Hx = Ay - 5 Hy = Ay 'EI:y=-(x-Ex)+Ey=a*x+b a = -1 b = Ex + Ey 'FJ:y=(x-Fx)+Fy=c*x+d c = 1 d = -Fx + Fy 'Iy=a*Ix+b=c*Ix+d Ix = (d - b) / (a - c) Iy = a * Ix + b If Ix <= Cx And By <= Iy Then 'GK:y=-(x-Gx)+Gy=a*x+b a = -1 b = Gx + Gy 'Jy=c*Jx+d=a*Jx+b Jx = (b - d) / (c - a) Jy = c * Jx + d 'HL:y=(x-Hx)+Hy=c*x+d c = 1 d = -Hx + Hy 'Ky=a*Kx+b=c*Kx+d Kx = (d - b) / (a - c) Ky = a * Kx + b 'EI:y=-(x-Ex)+Ey=a*x+b a = -1 b = Ex + Ey 'Ly=c*Lx+d=a*Lx+b Lx = (b - d) / (c - a) Ly = c * Lx + d 'menseki=IL^2 menseki = (Lx - Ix) * (Lx - Ix) + (Ly - Iy) * (Ly - Iy) wa = wa + menseki wa2 = wa2 + menseki * menseki kaisuu = kaisuu + 1 heikin = wa / kaisuu Picture3.Cls Picture3.Print Ay_min; "≦大きい正方形の1辺の長さ≦"; Ay Picture4.Cls If kaisuu > 1 Then hyoujunhensa = Sqr(heikin * heikin - wa2 / kaisuu) Picture4.Print "小さい正方形の面積の平均="; heikin; "cm2 (標準偏差="; hyoujunhensa; ")" End If Picture1.Cls Picture1.Line (Ax, Ay)-(Bx, By), vbBlack Picture1.Line -(Cx, Cy), vbBlack Picture1.Line -(Dx, Dy), vbBlack Picture1.Line -(Ax, Ay), vbBlack Picture1.Line (Ex, Ey)-(Ix, Iy), vbBlack Picture1.Line (Fx, Fy)-(Jx, Jy), vbBlack Picture1.Line (Gx, Gy)-(Kx, Ky), vbBlack Picture1.Line (Hx, Hy)-(Lx, Ly), vbBlack End If Next Ay End Sub Sub Command2_Click() Unload Me End Sub
解答・その2
(ペンネ-ム:足立of joy toy)
答えは ((5/√2)*2)2=50 だ!!! ウホッ 悟りの領域!
解答・その3
(ペンネ-ム:こざっぱ)
頂点を左記のように名づけます。
線分BKをKの方に伸ばし、線分CEと交わる点を Xとします(赤線)。
また、XとFをつなぎます(同じく赤線)。
このとき、三角形BCXは二等辺三角形となり、 (なぜなら角Cが直角で角CBX=45度より) 従って、AB=5cmなら、XEも5cmとなる。 (なぜなら、元の図形が正方形であるから)
また、線分EFも5cmであり、角E=直角から 三角形XEFは二等辺三角形となり、
線分XF=5√2cmとなる。 ‥‥①
一方、線分BXと、線分IFは平行であるので
(さすがにこれは証明不要)
それにそれぞれ直交する、線分XFと線分KLの
長さは等しい。 ‥‥②
①②より、中央の小さな正方形(網掛け部分)
の1辺の長さは、5√2となり、その面積は、
5√2×5√2 = 50
解答 面積は50cm2
解答・その4
(ペンネ-ム:杖のおじさん)
答え50cm2です
図について説明いたします。
線分AB CD DE FG GH IJ JK LA の長さは5㎝です。
線分CK=EI 、 線分BF=LH は平行線です。
∠ABL 、 ∠ALB は 45°です。
線分BL=MN=Xcm、線分MN=NP=PO=OM=Xcm
中心の正方形の面積S=MNOPは1辺Xcmの平方で求めます。
面積Sは直角三角形△LABの斜辺Xの二乗で求めます。
式は次のようになります。
X2=52+52=25+25=50
解答・その5
(ペンネ-ム:nao)
右の図のように動かせば、中の正方形の一辺は、5センチの直角二等辺三角形の 斜辺と等しいことがわかります。 そこで、中の正方形を、対角線が10センチのひし形と考えると、
10×10÷2=50
答え 50平方センチメートル
解答・その6
(ペンネ-ム:Mizutani)
折り紙の4角からそれぞれ対角線を引くと、同じ大きさの45度二等辺三角形が4つできる。 問題で求められている正方形は、その4つの三角形をそれぞれ5cmずつ外にずらした際に、4つの三角形の間にできる空間である。 したがって、元の正方形(折り紙)からはみ出した部分の4つの三角形の面積の合計が求めるべき正方形の面積となる。 はみ出した部分の三角形は同じく45度二等辺三角形であり、底辺(=高さ)5cmである。 したがって、1つの三角形の面積は、5×5×1/2となる。 つまり、4つの三角形の合計の面積(=求めるべき正方形の面積)は、
5×5×1/2×4=50
答えは50cm2となる。
解答・その7
(ペンネ-ム:ニトロ)
答え 50㎝2
□abcd-□echf×4=□fijk -左辺を変形させて
4×(□abcd/4-□echf)=□fijk ・・・①
ここで、□abcdの1辺をAとすると
□abcd/4は底辺をAとする直角二等辺三角形と定義できる。
辺bc=A、辺ec=A-5、
△cghは直角二等辺三角形だから、辺ch=辺cg=5
∴辺eg=辺ec+辺cg=A-5+5=Aとなり
△efgは底辺をAとする直角二等辺三角形となる
①式 4×(□abcd/4-□echf) = 4×(△efg-□echf) = 4×△cgh = 4×(5×5/2)=4×12.5=50㎝2
解答・その8
(ペンネ-ム:ちゃんこ鍋)
対角線を書き、中央の正方形の一辺を二分割して考える。 これをもとの正方形の辺に接触するまで平行移動させてみると 直角二等辺三角形となるため、その長さは5/ルート2cmと解る。 すると小さい正方形の一辺はその2倍で5ルート2cmと解る。
すると小さい正方形の面積は(5ルート2)の2乗で50cm2となる。
解答・その9
(ペンネ-ム:巷の夢)
大きな正方形に2本の対角線を引くと、小さな正方形は4個の更に小さな正方形 に分かれる。この更に小さな正方形の対角線は5cmであるから、これらを4個加えた 小さな正方形の対角線は10cmとなる。因って面積は10×10×1/2=50cm2 となる。
解答・その10
(ペンネ-ム:T_Tatekawa)
まず,右上がりの斜め線を図のように延長します. すると,図の黄色い線分の長さは 10cm になります. この黄色い線分は,中央部の正方形の,水平な対角線と平行で あるので,正方形の面積は
10*10/2 = 50 cm2
となります.
解答・その11
(ペンネ-ム:JSミル)
図のように,正方形ABCDの各頂点から5cmの点をEFGHとし,内部にできる正方形の各頂点をIJKL,正方形ABCDと正方形IJKLの各辺の延長線上の交点をMNOPとし,正方形ABCDの対角線の交点をQとする.
直角二等辺三角形AQBとEJNは合同であり,5cmだけ下方に移動しただけである.△BQCと△FKO,△CQDと△GLP,△DQAと△HIMも同じ関係である.従って,正方形ABCDの面積は△EJN+△FKO+△GLP+△HIMと同じである.これは,図の正方形ABCDからはみ出した部分,すなわち,△AEM,△BFN,△CGO,△DHP(これらはすべて合同)の面積の和が四角形IJKLの面積に等しいことを示している.
よって,求める面積は5×5×4÷2=50
答え50cm2
解答・その12
(ペンネ-ム:高橋 道広)
zu1のように 切り取り線をのばしてしまうと図の中の赤い線の長さが同じであ ることから中の正方形の対角線の長さが10cmであることがわかる よって面積は 1/2×10×10=50cm2となる
zu2のように 一辺の長さ10cmの正方形を切ったとすると 中には この正方形 の半分の面積を持つ正方形が出来る よって 中の正方形の面積は 50cm2
zu3のように赤い直角二等辺三角形を黒い図形にくっつけると 大きな二等辺三 角形が出来る。この二等辺三角形は 図のなかの 赤い二等辺三角形と合同であ るから 中の正方形の面積は赤い二等辺三角形4つ分と同じ面積を持つ よって 4×1/2×5×5=50cm2 となる
解答・その13
(ペンネ-ム:やなせ)
逆に行きますね問題は右の図ですが、それを苦しいですが底辺に沿ってそれぞれ5cmずらせば左のようになります。
正方形は直角二等辺三角形a,b,cが4個集まった物ですよね
それがそれぞれ5cmずれて出来た隙間の面積だから
右の図で言えば正方形からはみ出した直角二等辺三角形d,b,eが4個集まった物と同じはずです。
ずれたのが5cmですから辺d,bの長さも5cmのはず…
直角二等辺三角形d,b,eの面積は5×5÷2¬=12.5cm2
それが4個だから12.5×4=50cm2ですね
正方形の大きさには全く関係有りません
昔良くありました
直径10mの円があります。その1m外側に円を描けば円周は幾ら長くなるでしょう また地球の上に地上から1m離して綱を引けば長さは幾らでしょうなぁ~~んてね 関係ないか(笑)
解答・その14
(ペンネ-ム:ちかひで)
設問の形状は,正方形の対角線を引くことによりできる4個 の二等辺直角三角形を,それぞれ底辺沿いに右方向に5cmずら したことになる.従って,中央に対角線の長さ10cmの正方形が できる。その面積は,
10×10÷2=50
答:50cm2
解答・その15
(ペンネ-ム:三角定規)
右図の緑色の部分は明らかに合同だから,
中央の正方形の面積
=
=50 cm2 …[答]

解答・その16
(ペンネ-ム:teki)
答え 50cm2
考え方
真ん中の図形を正方形と考えると、どうしても辺の長さを計算したくなりますね。
でも、実は対角線の長さならすぐに求めることができます。
元の正方形の対角線を5cmずつ平行にずらしたのが、真ん中の正方形の辺 ですから、その対角線の長さは5×2=10cmです。
よって、真ん中の正方形の面積は10×10÷2=50cm2 ですね。
解答・その17
(ペンネ-ム:夜ふかしのつらいおじさん)
右の図のように、正方形に対角線を引きます。次に中央の正方形の頂点を通りもとの正方形の各辺に平行な線を引きます。すると灰色の部分は平行四辺形になります。この平行四辺形の短い方の辺の長さは5cmです。また中央の正方形の各辺を斜辺とする三角形は直角二等辺三角形です。すると、中央の正方形の辺の長さは5√2cmとなります。だからこの正方形の面積は50cm2です。
解答・その18
(ペンネ-ム:Toru)
大きな方の正方形を、中心に向かって縮めていって、まん中の正方形に接するとこ ろまで持ってくると、一辺が10cmになるので、まん中の正方形の面積はその半分 で50cm2 ----答え
解答・その19
(ペンネ-ム:蜘蛛の巣城)
与えられた正方形の外側に、小三角形を4枚つけ加えて上図を得ます。それは下図の4枚の直角二等辺三角形が、正方形の辺に沿って左回りにずれた形です。カメラのシャッターが開くようなイメージですね。従って、中央に生じた小正方形の面積は正方形の外側にはみ出た4枚の小三角形の面積の和ですから、正方形の辺の長さにかかわりなく 50cm2 です。もっとも、正方形の辺は 10cm 以上なければいけないことになりますか。
ところで、これは数学的論述でしょうか。書きながら疑問に捕らえられています。「説明」には、厳密さに関して要求される様々な水準というものがあるでしょうが、それにしてもくだけ過ぎているかもわかりません。くだけた説明を好む人ばかりなら、多分ユークリッド幾何学は成立しなかったのではないでしょうか。
正解者
杖のおじさん Toru JSミル Mizutani nao T_Tatekawa 浜田 明巳 ニトロ ちゃんこ鍋 巷の夢 teki 足立of joy toy やなせ 夜ふかしのつらいおじさん こざっぱ 蜘蛛の巣城 ちかひで 三角定規 高橋 道広
今月も多くの方々からの解答をどうもありがとうございました。 また、説明のためのイラストを作成していただいた方、どうもありがとうございました。
蜘蛛の巣城さんが、「カメラのシャッター」と表現してくださいましたが、 なかなかうまい表現だなと感心しました。面積を求めたい部分を直接測るのではなく、そこと同じ面積を持つ 他の部分を測ることで間接的に求めるというのは、いい手法ですよね。

 E-mail
E-mail
 top
top