Weekend Mathematics乛栤戣乛栤戣102
侾侽俀丏岄愇偺栤戣
俙偲俛偺俀偮偺敔偵敀愇偲崟愇偑擖偭偰偄傑偡丅 俙偺拞偵偼2700屄偑擖偭偰偄偰丄偦偺偆偪偺俁妱偑崟愇偱偡丅 俛偺拞偵偼1200屄偑擖偭偰偄偰丄偦偺偆偪偺俋妱偑崟愇偱偡丅 偄傑丄俛偺拞偐傜偄偔偮偐偺愇傪俙偵堏偟丄偦偺寢壥傪挷傋偨傜丄 俙偺拞偵偼崟愇偑係妱丄俛偺拞偵偼崟愇偑俋妱擖偭偰偄傑偟偨丅 俛偺拞偐傜俙偵堏偟偨崟愇偲敀愇偼丄偦傟偧傟偄偔偮偢偮偱偡偐丅
嶼悢侾侽侽偺擄栤丒婏栤
拞懞媊嶌
晲憼拞
島択幮僽儖乕僶僢僋僗
夝摎丒偦偺1
乮儁儞僱亅儉丗shrks乯
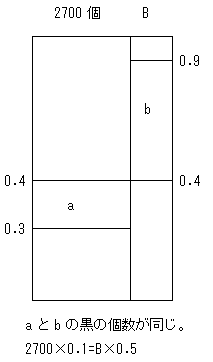
傕偲傕偲偁偭偨A偲B偺岄愇偺崟偺妱崌,堏摦偟偨屻偺妱崌偺曄壔偐傜 楢棫曽掱幃偑棫偰傜傟傑偡
傕偲傕偲A偺岄愇偼崟偑俁妱丄偲偄偆偙偲偼丂俀俈侽侽丂亊丂侽丏俁丂亖丂俉侾侽
傕偲傕偲B偺岄愇偼崟偑9妱丄偲偄偆偙偲偼丂侾俀侽侽丂亊丂侽丏俋丂亖丂侾侽俉侽
偙傟傪傕偲偵丂曽掱幃傪棫偰傑偡
崟傪X丄敀傪Y偲偡傞偲
堏摦屻偼A偺崟偺妱崌偑4妱丄B偑9妱偩偐傜
丂丂丂乮俀俈侽侽亄X亄Y乯亊侽丏係亖俉侾侽亄X
丂丂丂乮侾俀侽侽亅X亅Y乯亊侽丏俋亖侾侽俉侽亅X
偙傟傪夝偔偲丂丂X亖係俉俇丂Y亖俆係丂偲側傞
摎丂崟偑係俉俇屄丄敀偑俆係屄
夝摎丒偦偺2
乮儁儞僱亅儉丗偙偞偭傁乯
B偐傜A偵堏摦偟偨悢傪X丄偦偺撪偵娷傑傟傞崟偺悢傪Y偲偟偰 楢棫曽掱幃傪棫偰偰夝偄偰傒傑偟偨丅晛捠偺曽朄偱偡偹丅
乮2700+X乯*0.4=2700*0.3+Y丂乨嘆丂A偺戃偵偮偄偰偱偡
乮1200-X乯*0.9=1200*0.9-Y丂乨嘇丂B偺戃偵偮偄偰偱偡
嘆幃丂丂1080+0.4X=810+Y
嘆*10丂10800+4X=8100+10Y
丂丂丂丂10Y=4X+2700丂丂丂丂乨嘊
嘇幃丂丂1080-0.9X=1080-Y
嘇*10丂10800-9X=10800-10Y
丂丂丂丂10Y=9X丂丂丂丂丂丂乨嘋
嘋傪嘊偵戙擖
丂丂丂丂9X=4X+2700
丂丂丂丂X=540 丂丂丂丂丂丂乨嘍
嘍傪嘋偵戙擖
丂丂丂丂10Y=9*540
丂丂丂丂Y=486
B偐傜A傊堏偟偨慡懱偺悢(X)偼540屄
偦偺偆偪偺崟偺悢(Y)偼486屄
堏摦偟偨敀偺悢(X-Y)偼540-486=54屄丂
崟486屄丄敀54屄傪堏偟偨丂丂乮椆乯
夝摎丒偦偺3
乮儁儞僱亅儉丗僯僩儘乯
俙偺敔偺拞偵愇偑俀俈侽侽屄丄偦偺撪俁妱偑崟愇
丂亪崟愇偑俀俈侽侽亊侽丏俁亖俉侾侽
丂丂敀愇偑俀俈侽侽亊侽丏俈亖侾俉俋侽
俛偺敔偺拞偵愇偑侾俀侽侽屄丄偦偺撪俋妱偑崟愇
丂亪崟愇偑侾俀侽侽亊侽丏俋亖侾侽俉侽
丂丂敀愇偑侾俀侽侽亊侽丏侾亖侾俀侽
俙偺敔偐傜俛偺敔偵堏摦偝偣偨愇偺撪栿傪丂崟愇倶屄丄敀愇傪倷屄偲偡傞丅
偦偺寢壥俙偺敔偺拞偵崟愇偑係妱乮敀愇俇妱乯
丂丂丂丂俛偺敔偺拞偵崟愇偑俋妱乮敀愇侾妱乯偲側偭偨偺偱丄
俙偺敔偼丒丒丒俉侾侽亄倶丗侾俉俋侽亄倷亖係丗俇丒丒丒嘆
俛偺敔偼丒丒丒侾侽俉侽亅倶丗侾俀侽亅倷亖俋丗侾丒丒丒嘇
嘆傛傝丂丂俇亊乮俉侾侽亄倶乯亖係亊乮侾俉俋侽亄倷乯
丂丂丂丂丂丂丂係俉俇侽亄俇倶亖俈俆俇侽亄係倷
丂丂丂丂丂丂丂丂丂俇倶亅係倷亖俀俈侽侽
丂丂丂丂丂丂丂丂丂俁倶亅俀倷亖侾俁俆侽丒丒丒嘊
嘇傛傝丂侾亊乮侾侽俉侽亅倶乯亖俋亊乮侾俀侽亅倷乯
丂丂丂丂丂丂丂丂侾侽俉侽亅倶亖侾侽俉侽亅俋倷
丂丂丂丂丂丂丂丂丂亅倶亄俋倷亖侽丒丒丒嘋
嘊幃亄俁亊嘋幃傛傝
俁倶丂亅俀倷 亖侾俁俆侽 亄乯 亅俁倶亄俀俈倷 亖侽 俀俆倷 亖侾俁俆侽
丂丂丂丂丂丂亪倷亖俆係
嘋幃偵戙擖偟偰丂丂丂丂丂倶亖係俉俇
亙夝摎亜
俙偺敔偐傜俛偺敔傊堏摦偝偣偨愇偼丄崟愇係俉俇屄丒敀愇俆係屄
亙専嶼亜
俙偺敔偺拞恎
崟愇俉侾侽亄係俉俇亖侾俀俋俇
敀愇侾俉俋侽亄俆係亖侾俋係係乮寁俁俀係侽屄乯
侾俀俋俇亐俁俀係侽亖侽丏係
侾俋係係亐俁俀係侽亖侽丏俇丒丒丒俷俲
俛偺敔偺拞恎
崟愇侾侽俉侽亅係俉俇亖俆俋係
敀愇侾俀侽亅俆係亖俇俇乮寁俇俇侽屄乯
俆俋係亐俇俇侽亖侽丏俋
俇俇亐俇俇侽亖侽丏侾丒丒丒俷俲
埲忋
夝摎丒偦偺4
乮儁儞僱亅儉丗昹揷丂柧枻乯
俛偐傜崟愇傪倶屄丆敀愇傪倷屄堏偡偲偡傞丏俙丆俛偺拞偺崟愇偺屄悢偼丆偦傟偧傟丆
丂丂俀俈侽侽亊侽.俁亄倶亖侽.係(俀俈侽侽亄倶亄倷)乧乧乧(1)
丂丂侾俀侽侽亊侽.俋亅倶亖侽.俋(侾俀侽侽亅倶亅倷)乧乧乧(2)
丂(1)偐傜丆俆(俉侾侽亄倶)亖俀(俀俈侽侽亄倶亄倷)
丂丂亪係侽俆侽亄俆倶亖俆係侽侽亄俀倶亄俀倷
丂丂亪俁倶亅俀倷亖侾俁俆侽乧乧乧(1)'
丂(2)偐傜丆侾侽(侾侽俉侽亅倶)亖俋(侾俀侽侽亅倶亅倷)
丂丂亪侾侽俉侽侽亅侾侽倶亖侾侽俉侽侽亅俋倶亅俋倷
丂丂亪倶亖俋倷乧乧乧(2)'
丂(1)'偵戙擖偡傞偲丆俀俈倷亅俀倷亖侾俁俆侽
丂丂亪俀俆倷亖侾俁俆侽
丂丂亪倷亖俆係
丂(2)'偵戙擖偡傞偲丆倶亖係俉俇
丂偙傟傜偺倶丆倷偼嫟偵侽埲忋偺惍悢偱偁傝丆榓偑侾俀侽侽埲壓偱偁傞偺偱丆忦審傪枮偨偡丏
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂摎丏崟愇係俉俇屄丆敀愇俆係屄
乮暿夝乯俛偐傜俙偵堏偟偰傕丆崟愇偺妱崌偑俋妱偲曄傢傜側偐偭偨偺偱偁傞偐傜丆堏偟偨愇偺拞偺崟愇偺妱崌傕俋妱偱偁傞丏
丂崟愇傪倶屄丆敀愇傪倷屄堏偡偲偡傞偲丆倶亖俋倷
丂屘偵俙偺拞偺崟愇偺屄悢偼丆
丂丂俀俈侽侽亊侽.俁亄俋倷亖侽.係(俀俈侽侽亄俋倷亄倷)
丂丂亪俆(俉侾侽亄俋倷)亖俀(俀俈侽侽亄侾侽倷)
丂丂亪係侽俆侽亄係俆倷亖俆係侽侽亄俀侽倷
丂丂亪俀俆倷亖侾俁俆侽
丂丂丒丒丒
乮暿夝乯僄僋僙儖偺儅僋儘傪巊偭偰夝偒傑偟偨丏乮僐僺乕仌揬傝晅偗偡傞嵺偼丆慡妏偺嬻敀傪敿妏偵偟側偔偰偼側傝傑偣傫乯
Option Explicit Const A As Integer = 2700 Const B As Integer = 1200 Sub Macro1() 丂丂Sheets("Sheet1").Select 丂丂Cells(1, 1).Value = 0 丂丂Range("A1").Select 丂丂Dim A_white As Integer 丂丂Dim A_black As Integer 丂丂Dim B_white As Integer 丂丂Dim B_black As Integer 丂丂Dim A_white0 As Integer 丂丂Dim A_black0 As Integer 丂丂Dim B_white0 As Integer 丂丂Dim B_black0 As Integer 丂丂Dim black As Integer 丂丂Dim white As Integer 丂丂A_black = A * 0.3 丂丂A_white = A - A_black 丂丂B_black = B * 0.9 丂丂B_white = B - B_black 丂丂For white = 0 To B_white 丂丂丂For black = 0 To B_black 丂丂丂丂A_white0 = A_white + white 丂丂丂丂A_black0 = A_black + black 丂丂丂丂B_white0 = B_white - white 丂丂丂丂B_black0 = B_black - black 丂丂丂丂If A_black0 / (A_white0 + A_black0) = 0.4 Then 丂丂丂丂丂If B_black0 / (B_white0 + B_black0) = 0.9 Then 丂丂丂丂丂丂Cells(1, 1).Value = Cells(1, 1).Value + 1 丂丂丂丂丂丂Cells(Cells(1, 1).Value, 2).Value = white 丂丂丂丂丂丂Cells(Cells(1, 1).Value, 3).Value = black 丂丂丂丂丂End If 丂丂丂丂End If 丂丂丂Next black 丂丂Next white End Sub嶲峫暥專傪尒傞偲丆偙偺栤戣偼嶼悢偺曽朄偱夝偐側偗傟偽側傜側偐偭偨偺偱偟傚偆偐丠
夝摎丒偦偺5
乮儁儞僱亅儉丗嵅栰堯怣乯
B偺拞偐傜A偵堏偟偨崟愇偲敀愇傪偦傟偧傟丂x 屄丆y 屄偲偡傞偲丄忦審傛傝
偑惉傝棫偮丏 (1)傛傝
丂丂丂6x=4y+2700丂丂丂(3)
(2)傛傝
丂丂丂x=9y丂丂丂(4)
(4)傪(3)偵戙擖偡傞偲
丂丂丂54y=4y+2700
丂丂丂亪丂y=54
偙傟傪(4)偵戙擖偡傞偲
丂丂丂x=486
傛偭偰丆B偺拞偐傜A偵崟愇傪係俉俇屄丆敀愇傪俆係屄堏偟偨丏丂乮摎乯
夝摎丒偦偺6
乮儁儞僱亅儉丗嶰妏掕婯乯
俙(崟810丆敀1890)丆俛(崟1080丆敀120)
俛偐傜俙偵崟愇傪x屄丆敀愇傪y屄堏偟偨偲偡傞偲丆戣堄傛傝
嘇傛傝x亖9y 偱丆偙傟偲嘆偲傛傝丆x亖486丆y亖54丅丂丂[摎] 崟愇486屄丆敀愇54屄丂
夝摎丒偦偺7
乮儁儞僱亅儉丗岼偺柌乯
B偐傜A偵堏偟偨屄悢傪C偲偡傞偲敀偼偦偺侾妱傝丄崟偑俋妱傝偱側偗傟偽巆偭偨B偺崟偺 妱崌俋偲側傝傑偣傫丅場偭偰丄A偵墬偗傞崟偺妱崌偼丄
丂丂丂丂(2700亊3/10 + C亊9/10)/(2700 +C) =4/10 =2/5 偲側傞丅
偙偺曽掱幃傪夝偄偰丄C=540傪摼傞丅 埲忋傛傝媮傔傞崟愇偼486丄敀愇偼54偱偁傞丅
丂夝摎丒偦偺8
乮儁儞僱亅儉丗暷傐傫乯
戣堄傛傝丆
敔A偵偼丆崟810屄丆敀1890屄偱丆寁2700屄
敔B偵偼丆崟1080屄丆敀120屄偱丆寁1200屄
敔B偐傜A偵堏偟偨愇偺悢傪x偲偟偰丆戣堄傛傝曽掱幃傪嶌傞偲丆
丂丂丂乮2700+倶乯亊0.4+乮1200-x乯亊0.9亖810+1080
丂丂丂x=540
堏偟偨屻偺敔A偵偼丆
2700+540亖3240屄
偦偺偆偪丆4妱偑崟偩偐傜丆崟偺悢偼
3240*0.4亖1296屄
傕偲傕偲丆敔A偵偼丆崟偼810屄偁偭偨偐傜丆
堏偟偨愇偺撪栿偼丆
崟486屄丆敀54屄
夝摎丒偦偺9
乮儁儞僱亅儉丗Mizutani乯
乮夝摎乯
乮侾乯
俙偺敔偵擖偭偰偄傞敀愇偺悢丗俀俈侽侽亊侽丏俈亖侾俉俋侽屄
丂丂丂丂丂丂丂丂丂崟愇偺悢丗俀俈侽侽亊侽丏俁亖俉侾侽屄
俛偺敔偵擖偭偰偄傞敀愇偺悢丗侾俀侽侽亊侽丏侾亖侾俀侽屄
丂丂丂丂丂丂丂丂丂崟愇偺悢丗侾俀侽侽亊侽丏俋亖侾侽俉侽屄
乮俀乯
俛偐傜俙傊堏偟偨愇偺悢傪倃偲偡傞丅
堏偟偨偍屻偺俛偺敔偺敀愇偲崟愇偲偺斾棪偑堏偡慜偲曄傢偭偰偄側偄乮侾丗俋乯偙 偲偐傜丄倃偺敀愇偲崟愇偺斾棪傕侾丗俋偲側傞丅
乮俁乯
俙偵堏偟偨屻偺慡懱偺愇偺悢偼俀俈侽侽亄倃偲側傞丅
傑偨丄俙偵堏偟偨屻偺敀愇偺悢偼丄侾俉俋侽亄侽丏侾倃偲側傞丅
乮係乯
俙偵堏偟偨屻偺敀愇偲崟愇偲偺斾棪偼俇丗係偱偁傞偙偲偐傜丄
丂丂丂侾俉俋侽亄侽丏侾倃亖侽丏俇乮俀俈侽侽亄倃乯
偺幃偑惉傝棫偪丄夝偼丄倃亖俆係侽偲側傞丅
乮俆乯
偟偨偑偭偰丄俛偺拞偐傜俙偵堏偟偨崟愇偲敀愇偼乮俀乯傛傝丄偦傟偧傟丄
丂丂丂崟愇丗俆係侽亊侽丏俋亖係俉俇
丂丂丂敀愇丗俆係侽亊侽丏侾亖俆係
偲側傞丅
埲忋丅
夝摎丒偦偺10
乮儁儞僱亅儉丗偡側憼乯
摎偊丗堏摦偟偨崟愇係俉俇屄丄敀愇俆係屄偺寁俆係侽屄
拲栚偡傞揰偼丄堏摦屻偺俛偺愇偺斾棪丅偙傟偑堏摦慜屻偱曄傢偭偰偄側偄偲 偄偆偙偲偼丄庢傝弌偟偨愇偵娷傑傟傞敀崟偺愇偺斾棪偑尦偺崟俋妱丄敀侾妱 偲摨偠偱偁傞偲偄偆偙偲丅偮傑傝丄x屄偺愇傪庢傝弌偟偨偲偒 偦偺峔惉斾偼崟愇0.9x屄丄敀愇0.1x屄偲側傜側偗傟偽偍偐偟偄丅 偦偺偆偊偱丄堏摦屻偺俙偺崟愇偺斾棪偑係妱偵側傞傛偆偵倶傪寛掕偡傟偽傛偄丅
堏摦慜偺俙偺愇偺峔惉偼崟810屄丄敀1890屄偱偁傝丄偙傟偑堏摦屻偼 崟愇(810+0.9x)屄丄敀愇(1890+0.1x)屄偱崌寁偑(2700+x)屄偵側傝丄 崟愇偺妱崌偑係妱偵側傞偺偩偐傜
丂丂丂(810+0.9倶)亐(2700+x乯亊100亖0.4
偙傟傪枮偨偡x偼俆係侽屄丅傛偭偰堏摦偟偨愇偼
丂丂丂崟丗540亊0.9亖486屄
丂丂丂敀丗540亊0.1亖54屄
偵側傞丅
夝摎丒偦偺11
乮儁儞僱亅儉丗kiyo乯
810+0.9*x=0.4*(2700+x)
x=540
540*0.9=486
540*0.1=54
摎偊丂崟愇丂係俉俇屄丅敀愇丂俆係屄丅
夝摎丒偦偺12
乮儁儞僱亅儉丗傾僢僠儑儞僽儕働乯
摎丏崟愇偲敀愇偼丄偦傟偧傟係俉俇屄丄俆係屄丅
夁掱
B偺拞偐傜愇傪A偵堏偟偨屻偺B偺拞偺崟愇偺妱崌偑丄堏偡慜偺妱崌偲曄傢傜側 偐偭偨偺偱丄堏偟偨愇偺崟愇偺妱崌傕俋妱偩偲傢偐傞丅傛偭偰丄堏偟偨崟愇偲敀 愇偺屄悢偼丄偦傟偧傟俋亊N屄丄N屄乮N偼惓偺惍悢乯偲昞偣傞偺偱丄堏偟偨屻偺A 偺拞偺崟愇偼丄乮俀俈侽侽亊侽丏俁亄俋亊N乯屄偲側傞丅 堏偟偨屻丄A偺拞偵偼崟愇偑係妱偩偐傜丄
丂丂丂乮俀俈侽侽亄侾侽亊N乯亊侽丏係亖俀俈侽侽亊侽丏俁亄俋亊N
偙傟傪夝偔偲丂N=俆係丅 偙偙偱丄堏偟偨愇偺憤悢侾侽亊俆係亖俆係侽屄偼丄巒傔B偺拞偺侾俀侽侽屄傛傝 傕彮側偄偺偱揔偡丅 屘偵丄B偺拞偐傜A偵堏偟偨崟愇偲敀愇偼丄偦傟偧傟俋亊俆係亖係俉俇屄丄俆係屄 偲媮傑傞丅
夝摎丒偦偺13
乮儁儞僱亅儉丗Toru乯
丂敔B偺崟愇偲敀愇偺妱崌傪曐偭偨傑傑堏偟偰偄傞偺偱丄敀愇傪X屄堏偟偨偲偡傟偽丄 崟愇偼9X屄丄慡懱偱堏偟偨悢偼10X屄偲側傞丅
丂寁嶼傪妝偵偡傞偨傔偵(偲尵偭偰傕戝偟偨寁嶼偱偼偁傝傑偣傫偑) 敔A偺堏偡慜偺憤悢偑100偩偭偨応崌偱寁嶼偡傞偲乮偙偺応崌偼X偼惍悢偱側偔偲傕傛 偄乯丄堏偟偨寢壥丄敔A偺憤悢100+10X 丂敀愇70+X偱丄敀愇偑俇妱偵側偭偨偺偩偐傜丄
丂100+10X丗70+X=10丗6佁10+X丗70+X= 1丗6佁10+x丗60=1丗5 偙傟偐傜丂X=2
傛偭偰2700屄偺応崌偼2亊27=54丂崟愇偼54亊9=486丂
丂偡側傢偪丄崟愇486屄丂敀愇54屄丂乗乗乗乗摎偊丂偙傟傜偺榓偼1200傛傝彫偝偔偰丄 戣堄偵揔偡丅
夝摎丒偦偺14
乮儁儞僱亅儉丗俰俽儈儖乯
B偐傜岄愇傪堏偟偨屻傕岄愇偺斾棪偑摨偠偙偲偐傜丆堏偟偨敀偄岄愇偺屄悢傪倃偲偡 傞偲丆堏偟偨岄愇偺憤悢偼10倃偲昞偣傑偡丏廬偭偰丆A偺敀偄岄愇偵偮偄偰偺斾棪偼 堏摦屻偵丆
丂丂丂乮270亊7亄倃乯/ (2700亄10倃)亖6/10
偲側傝傑偡丏偙傟傪丆夝偄偰倃亖54
摎偊偼崟偄岄愇486屄丆敀偄岄愇54屄偲側傝傑偡丏
夝摎丒偦偺15
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂丂丂敀愇丂俆係屄丄丂崟愇丂係俉俇屄丂
B偺敔偺敀愇傪侾偮A偺敔偵堏摦偡傞帪偵崟愇傕俋偮堏摦偝偣傑偡丅摨偠斾棪偱堏摦偟 傑偡偺偱堏偟廔偭偨寢壥傕B偺敔偺崟愇偺妱崌偼俋妱偲側傝傑偡丅 堏偡夞悢傪倃偲偡傞偲A偺敔偺崟愇偺妱崌偑堏摦屻係妱側偺偱師偺幃偑惉傝棫偪傑偡丅
丂丂丂乮俉侾侽亄俋倃乯乛乮俀俈侽侽亄侾侽倃乯亖侽丏係
丂丂丂俉侾侽亄俋倃亖侾侽俉侽亄係倃
丂丂丂俆倃亖俀俈侽
丂丂丂倃亖俆係
敀愇傪俆係屄丂A偺敔偵堏摦偝偣傑偡丅
崟愇傪俆係亊俋亖係俉俇屄丂A偺敔偵堏摦偝偣傑偡丅
堏摦屻偺敔偺拞偺岄愇偺悢
A丂偺敔偵偼丂俀俈侽侽亄俆係亄係俉俇亖俁俀係侽屄
B丂偺敔偵偼丂侾俀侽侽亅俆係亅係俉俇亖俇俇侽屄
夝摎丒偦偺16
乮儁儞僱亅儉丗teki乯
摎偊丂崟愇丂係俉俇屄丂丂敀愇丂俆係屄
夝朄
丂堏摦偟偨慜屻偺俛偺敀丗崟偺斾棪偑曄傢偭偰偄側偄偙偲偐傜丄堏摦偟偨敀愇偲崟愇 偺斾偼丄侾丗俋丅
丂屻偼丄擹搙偺寁嶼傪峴偆偺偲摨偠梫椞偱丄埲壓偺曽掱幃傪夝偒傑偟偨丅
丂堏摦偟偨敀愇偺悢傪倶偲偡傞偲丄
丂丂丂丂乮俉侾侽亄俋倶乯亐乮俀俈侽侽亄侾侽倶乯亖侽丏係
丂偙傟偐傜丄倶亖俆係偑媮傑傝傑偡丅
丂偮傑傝丄堏摦偟偨敀愇偼俆係屄丄崟愇偼偦偺俋攞偱偡偺偱丄係俉俇屄丂偱偡丅
丂偙偺栤戣丄堏摦偟偨慜屻偺俛偺敀丗崟偺斾棪偑曄傢偭偰偄側偄偙偲偵婥偯偔偐偳偆 偐偺栤戣偱偡偹丅
夝摎丒偦偺17
乮儁儞僱亅儉丗帥榚將乯
俙敔偼丂俀俈侽侽屄偱丄崟愇偼丂俁妱偩偐傜丂俉侾侽屄丂敀愇偼丂俈妱偱丂侾俉俋侽屄
俛敔偺崟愇偲敀愇偺斾棪偼丂崟俋妱丂敀侾妱偱偁傞偑丂偙偺斾棪傪曄偊傞偙偲側偔 丂偄偔偮偐偺愇傪庢傝弌偟俙敔傊堏偡丄偦偺帪偺敀愇偺屄悢傪丂俶偲偍偗偽丂崟愇偼丂俋俶丂偲彂偗傞丅 偱丄俙敔偺丂崟俁妱丂敀俈妱丂偼丂崟係妱丂敀俇妱偵曄傢偭偨偐傜
丂丂丂(810+ 9N) 丗(1890+N) = 4丗6
偲棫幃偱偒傞丅 偙傟傪夝偄偰丂丂丂俶亖俆係屄丂丂丂丂丂俋俶亖丂係俉俇屄
偡側傢偪堏偟偨丂崟愇偼丂係俉俇屄丂丂敀愇偼丂俆係屄偱偡丅
夝摎丒偦偺18
乮儁儞僱亅儉丗T_Tatekawa乯
A 偺拞恎偼丆
丂丂丂崟丗2700 * 0.3 = 810 屄
丂丂丂敀丗2700 * 0.7 = 1890 屄
偱偡丏B 偺拞恎偼
丂丂丂崟丗1200 * 0.9 = 1080 屄
丂丂丂敀丗1200 * 0.1 = 120 屄
偱偡丏
B 偺拞偐傜 A 偺拞偵愇傪堏偡嶌嬈傪峫偊傞偲丆堏偡慜偲屻偱 B 偺拞偺愇偺斾棪偼曄傢偭偰偄傑偣傫丏偮傑傝丆崟偲敀傪 9:1 偺妱崌偱 A 偺拞偵堏偟偨帠偵側傝傑偡丏
偦偙偱丆堏偟偨崟偲敀偺愇偺屄悢傪偦傟偧傟丆9x 屄偲 x 屄偵 偟傑偡丏x 偼 120 埲壓偺帺慠悢偱偡丏
愇傪堏偟偨屻偺 A 偺拞恎偺崟偲敀偺愇偺悢偺斾偼 4:6 偱偡偺偱丆
丂丂丂810 + 9x : 1890 + x = 4 : 6
偱偡丏傛偭偰
丂丂丂6*(810 + 9x) = 4*(1890 + x)
惍棟偟偰
丂丂丂0 x = 2700
丂丂丂x = 54
埲忋偐傜堏偟偨愇偺屄悢偼丂崟 54*9 = 486屄丆敀 54 屄丏
夝摎丒偦偺19
乮儁儞僱亅儉丗倠倕値乯
俛偐傜俙偵堏偡慜偺俙偺敔偵偼丄
丂丂丂崟愇丂俉侾侽屄
丂丂丂敀愇丂侾俉俋侽屄
偑擖偭偰偄傞丅
堏偡慜傕丄堏偟偨屻傕丄俛偺敔偵偼俋丗侾偺妱崌偱擖偭偰偄傞偨傔丄俛偐傜俙偵堏 偟偨崟愇偲敀愇偺妱崌傕俋丗侾偲側傞丅
偙偙偱丄堏偟偨敀愇偺悢傪倃丂偲偡傞偲丄崟愇偺悢偼俋倃丂偲側傞丅
堏偟偨偁偲偺俙偺敔偺拞偼丄
丂丂丂崟愇丂丗丂乮俉侾侽亄俋倃乯
丂丂丂敀愇丂丗丂乮侾俉俋侽亄倃乯
崟愇偺妱崌偼係妱偺偨傔丄
丂丂丂乮俉侾侽亄俋倃乯乛乷乮俉侾侽亄俋倃乯亄乮侾俉俋侽亄倃乯乸亖侽丏係
偙傟傪夝偄偰丄
丂丂丂倃亖俆係
俛偐傜俙偵堏偟偨愇偺悢偼丄
丂丂丂崟愇偺悢丂係俉俇屄
丂丂丂敀愇偺悢丂丂俆係屄
偲側傞丅
夝摎丒偦偺20
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
弶傔偺忬懺
俙偺敔 俛偺敔 寁 敀 侾俉俋侽 侾俀侽 俀侽侾侽 崟 俉侾侽 侾侽俉侽 侾俉俋侽 寁 俀俈侽侽 侾俀侽侽 俁俋侽侽
堏摦偟偨屻偺忬懺
俙偺敔 俛偺敔 寁 敀 侾俋係係 俇俇 俀侽侾侽 崟 侾俀俋俇 俆俋係 侾俉俋侽 寁 俁俀係侽 俇俇侽 俁俋侽侽
俛偺敔偺拞偐傜俙偺敔偵堏偡敀愇傪倵屄偲偟傑偡丅
愇傪堏摦偝偣偨屻傕俛偺敔偺拞偺愇偺屄悢偺斾偼丄敀丗崟亖侾丗俋側偺偱丄俛偺敔偺拞偐傜俙偵堏偡崟愇偺屄悢偼俋倵屄偱偡丅
堏摦屻偺俙偺敔偺拞偺愇偺屄悢偵偮偄偰丄
丂丂丂乮俉侾侽亄俋倵乯丗乮俀俈侽侽亄侾侽倵乯亖係丗侾侽
偙傟傪夝偄偰丄倵亖俆係丄俋倵亖係俉俇
俛偺拞偐傜俙偵堏偟偨崟愇偲敀愇偼丄係俉俇屄偲俆係屄偱偡丅
夝摎丒偦偺21
乮儁儞僱亅儉丗偗偄偨傠偆乯
俙偺崟愇偼丂2700亊3/10亖810丂偱810屄丄敀愇偼丂2700亅810亖1890丂偱1890屄
俛偐傜偄偔偮偐堏偟偰丄妱崌偑曄傢傜偢崟愇俋妱側偺偱丄
堏偟偨愇偺拞偩偗偱偺敀崟偺妱崌傕丂敀丗崟亖1丗9丂
傛偭偰敀愇偺悢傪 a 偲偍偔偲丄崟愇偼丂9a
堏摦屻偺俙偺敔偺拞偼丂崟愇丂810亄9a 屄丄敀愇丂1890+a 屄
堏摦屻偺俙偺崟愇偼係妱側偺偱崟丗敀亖4丗6亖2丗3
幃
(810+9a)/(1890+a)亖2/3
a=54
崟愇偼丂54亊9亖486丂偱486屄
摎偊
堏摦偟偨崟愇偼486屄丄敀愇偼54屄
夝摎丒偦偺22
乮儁儞僱亅儉丗崅嫶丂摴峀乯
夝摎丂丂崟愇丂486屄丂敀愇丂54屄
夝愢丂
B偺岄愇偺敀崟偺斾偼曄傢傜側偄偺偱丂敀崟傪1:9偺妱崌偱敳偒弌偟偰A偵堏偟偰 偄傞偲峫偊傜傟傞丅
岄愇偺妱崌傪擹搙丂偲峫偊傞偲丂擹搙30%偺傕偺2700屄偲擹搙90亾偺傕偺傪崿偤 偰擹搙40亾偺傕偺傪嶌傞栤戣偵撉傒懼偊傞偙偲偑偱偒傞 傛偭偰丂揤攭嶼偱
丂丂丂丂10亊2700=50亊M偐傜
M=540屄偑B偐傜丂A偵堏偟偨屄悢偱
崟愇偼丂540亊0.9=486屄丂敀愇偼540亊0.1=54屄
夝摎丒偦偺23
乮儁儞僱亅儉丗彫妛柤扵掋乯
傕偲揤攭弇偝傫 乽偙傟偼丄怘墫悈偺崿偤崌傢偣傒偨偄側栤戣偩偐傜揤攭嶼巊偆偲娙扨偵夝偗傞偺傛丅夝偒曽朰傟偨偗偳丅乿
傕偲柺愊弇孨 乽傏偔偺捠偭偨弇偱偼丄柺愊嶼偲偐仜仩嶼偲偐偄偆偺偱廗偭偨傛丅 偊乕偲丄俀偮偺柺愊偑摨偠偵側傞偼偢側傫偩偗偳丅偛傔傫両偪傖傫偲愢柧偱偒側偄丅乿
側傫偱傕曽掱幃孨乮尰栶乯 乽俛偺拞偐傜俙偵堏偟偨崟愇偲敀愇偺崌寁傪倶屄偲偍偔偲丄 (2700+x)*4 = 2700*3+9x偵側傞偹丅偁偲丄撪暘揰偺岞幃偭偰偄偆偺傕偁傞偗偳丅乿
傒傫側朰傟偨偝傫 乽側傫偱丄岄愇偑揤攭偵側傞偺丠柺愊偵側傞偺丠曽掱幃偼堦斣嬯庤偩偹丅 帺枬偠傖側偄偑岞幃偼偤乕傫傇妛峑偵梐偗偰偒偪傑偭偨偤丅乿
愢柧學 乽崲傝傑偟偨偹丅偲傝偁偊偢丄
仠仠仠仜仜仜仜仜仜仜
崟愇偼壗妱偱偟傚偆偐丅乿
慡堳 乽俁妱偱偡両乿
愢柧學 乽係妱偩偲丄
仠仠仠仠仜仜仜仜仜仜
偱偡偹丅乿
慡堳 乽堎媍側偟両乿
愢柧學 乽偱偼丄
仠仠仠仜仜仜仜仜仜仜傪
仠仠仠仠仜仜仜仜仜仜偵偡傞偵偼偳偆偟傑偡偐丅乿
傒傫側朰傟偨偝傫 乽係妱偵偡傞偵偼丄敀愇1屄傪崟愇偵戙偊傝傖偄偄偺偝丅乿
愢柧學 乽偦偺捠傝偱偡丅
仠仠仠仜仜仜仜仜仜仜偐傜
敀愇傪1屄弌偟偰丄戙傢傝偵崟愇傪1屄傕傜偆偲丄崟愇偑係妱偵側傝傑偡丅 偱偼丄 仠仠仠仠仠仠仠仠仠仜傪
仠仠仠仠仜仜仜仜仜仜偵偡傞偵偼丠乿
傒傫側朰傟偨偝傫 乽崟愇俆屄傪敀愇偲岎姺偡傝傖偄偄丅乿
愢柧學 乽偦傟偱偼丄
仠仠仠仜仜仜仜仜仜仜
仠仠仠仜仜仜仜仜仜仜
仠仠仠仜仜仜仜仜仜仜
仠仠仠仜仜仜仜仜仜仜
仠仠仠仜仜仜仜仜仜仜
偲丄
仠仠仠仠仠仠仠仠仠仜
偱愇傪岎姺偟偰丄偳偺侾侽屄傕崟愇偑係屄偵側傞傛偆偵偱偒傑偡偐丅乿
傒傫側朰傟偨偝傫 乽偊乕偲丄弌棃偦偆偩側丅
仠仠仠仠仜仜仜仜仜仜
仠仠仠仠仜仜仜仜仜仜
仠仠仠仠仜仜仜仜仜仜
仠仠仠仠仜仜仜仜仜仜
仠仠仠仠仜仜仜仜仜仜
仠仠仠仠仜仜仜仜仜仜
妋偐偵姩掕偼崌偭偰傜丅 乿
愢柧學 乽偲偄偆偙偲偱丄崟愇偑俁妱偺岄愇俆侽屄偲崟愇偑俋妱偺岄愇侾侽屄傪 崿偤傞偲丄崟愇偑係妱偵側傝傑偡偹丅乿
慡堳 乽堎媍側偟両乿
愢柧學 乽偱偼丄偵偣傫側側傂傖偭偙丒丒丒乿
傒傫側朰傟偨偝傫 乽偪傚偭偲懸偭偨両姩掕側傜擟偣偰偔傟両俆侽屄偺偲偒 侾侽屄側傫偩偐傜丄俀俈侽侽屄側傜丄俆偱妱偭偰 俆係侽屄偺岄愇傪崿偤偨傫偩側丅俙偵堏偟偨敀愇偼 俆係侽亐侾侽亖俆係屄丄崟愇偼俆係侽亅俆係亖係俉俇屄偱偄丅乿
愢柧學 乽懍偄偱偡偹丅彆偐傝傑偟偨丅奆偝傫崌揰偟傑偟偨偐丅乿
慡堳 乽崌揰両乿
乮庼嬈偺屻乯
側傫偱傕曽掱幃孨乮尰栶乯 乽係偼俁偲俋傪侾丗俆偵撪暘偡傞揰偩偐傜丄 撪暘揰偺岞幃乮儈僉僔儞僌偺岞幃乯4=3*5/(1+5)+9*1/(1+5) 儃僜儃僜丒丒丒乿
傒傫側朰傟偨偝傫 乽偍乕偄丄傂偲傝偛偲偄偭偰側偄偱丄偙偭偪偵偒側傛丄 岄傪巒傔傞偐傜偝丅乿
側傫偱傕曽掱幃孨乮尰栶乯 乽偼乕偄丄巘彔丅乿
夝摎丒偦偺24
乮儁儞僱亅儉丗儎儞儅乯
曽掱幃傪棫偰傟偽娙扨偵夝偗傞偺偱丄曽掱幃傪巊傢偢偵媮傔傞丅
丂丂(1)崟愇偺崌寁偼侾俉俋侽偱偁傞丅乮敀愇偺崌寁偼俀侽侾侽偱偁傞乯
丂丂(2)愇偺屄悢乮帺慠悢乯偲係妱偲俋妱偲偄偆偙偲偐傜崟愇媦傃敀愇偺慡悢偼彮側偔偲傕壓侾寘栚偼僛儘偱偁傞丅
埲忋偺偙偲偐傜A敔偺崟愇偑係妱丄B偺敔偺崟愇偑俋妱偺帪丄偦偺崌寁偑 侾俉俋侽偲側傞A偺敔偺慡悢枖偼B偺敔偺慡悢傪媮傔傟偽傛偄丅
摎偊丄崟愇丂係俉俇屄丄敀愇丂俆係屄
夝摎丒偦偺25
乮儁儞僱亅儉丗nao乯
曽掱幃傪偨偰偰夝偔側傜丄B偐傜堏偟偨屄悢傪倃偲偍偔偲
丂丂丂乮俀俈侽侽亄倃乯丒乮係乛侾侽乯亖俀俈侽侽丒乮俁乛侾侽乯亄乮俋乛侾侽乯丒倃
丂丂丂侾侽俉侽亄乮係乛侾侽乯丒倃亖俉侾侽亄乮俋乛侾侽乯丒倃
丂丂丂乮侾乛俀乯丒倃亖俀俈侽
丂丂丂倃亖俆係侽
崟愇偺屄悢丂俆係侽亊乮俋乛侾侽乯亖係俉俇
敀愇偺屄悢丂俆係侽亊乮侾乛侾侽乯亖俆係
偲側傝傑偡丅
嶼悢偺峫偊曽偱夝偔偲丄俙偺俁妱偐傜係妱偵傆偊偨崟偺屄悢偱偁傞
丂丂丂俀俈侽侽亊乮侽丏係乕侽丏俁乯亖俀俈侽
偼丄俛偐傜堏偭偰偒偨晹暘偱俋妱偐傜係妱偵尭偭偨崟偺屄悢偲摍偟偔側傝傑偡丅 偩偐傜丄
丂丂丂乮俛偐傜堏偭偰偒偨晹暘乯亊乮侽丏俋乗侽丏係乯亖俀俈侽
丂丂丂俀俈侽亐侽丏俆亖俆係侽
俛偐傜堏偭偰偒偨晹暘偼俆係侽屄偩偲暘偐傝傑偡丅
偁偲偼丄崟丂俆係侽亊侽丏俋亖係俉俇丂丂敀丂俆係侽亊侽丏侾亖俆係丂偱偡丅
偙偺栤戣偼丄乽俁侽亾偺怘墫悈俀俈侽侽僌儔儉偵俋侽亾偺怘墫悈傪傑偤偨傜係侽亾偵 側偭偨丅俋侽亾偺怘墫悈傪壗僌儔儉傑偤偨偐乿偲偄偆栤戣偲摨偠偩偲偍傕偄傑偡丅
夝摎丒偦偺26
乮儁儞僱亅儉丗抴鍋偺憙忛乯
A丄B偦傟偧傟偺敔偺崟愇敀愇傪埲壓偺傛偆偵攝抲偟傑偡丅
堦峴10屄偺岄愇偱A270峴丄B120峴丅崟愇敀愇偺儅乕僋偼偍暘偐傝偱偡偹丅
A B 仐仐仐仏仏仏仏仏仏仏 仐仐仐仐仐仐仐仐仐仏 仐仐仐仏仏仏仏仏仏仏 仐仐仐仐仐仐仐仐仐仏 丒丒丒丒 丒丒丒丒 丒丒丒丒 仐仐仐仐仐仐仐仐仐仏 仐仐仐仏仏仏仏仏仏仏 丂
敔B偐傜敔A偵岄愇傪堏摦偝偣偰傕B偺崟敀斾棪偼曄壔側偟丅 偲偄偆偙偲偼B偺値峴傪偦偭偔傝A偵忋忔偣偟偨傢偗偱偡丅
仐仐仐仐仐仐仐仐仐仏 仐仐仐仐仐仐仐仐仐仏 丒丒丒丒 仐仐仐仐仐仐仐仐仐仏 仐仐仐仏仏仏仏仏仏仏 仐仐仐仏仏仏仏仏仏仏 丒丒丒丒 丒丒丒丒 仐仐仐仏仏仏仏仏仏仏
A偺崟敀斾棪偑4妱6妱偵曄壔偟偨偺偱偡偐傜丄忋恾偺怓偮偒晹暘傪擖傟懼偊傟偽傛偄傢偗偱偡丅廬偭偰
丂丂丂丂丂丂丂丂丂丂丂丂5値亖270
丂丂丂丂丂丂丂丂丂丂丂丂 値亖54
偡側傢偪54峴忋忔偣丅崟愇486屄丄敀愇54屄偺堏摦丅
惓夝幰
岼偺柌 shrks 忨偺偍偠偝傫 暷傐傫 偙偞偭傁 T_Tatekawa teki nao Toru Mizutani 僯僩儘 偡側憼 帥榚將 俰俽儈儖 昹揷丂柧枻 kiyo 嵅栰堯怣 傾僢僠儑儞僽儕働 彫妛柤扵掋 栭傆偐偟偺偮傜偄偍偠偝傫 偗偄偨傠偆 倠倕値 嶰妏掕婯 崅嫶丂摴峀 儎儞儅 抴鍋偺憙忛
懡偔偺曽偼丄曽掱幃傪棫偰偰夝偄偰偔偩偝偄傑偟偨丅
乽堏摦偟偨崟愇偺悢傪倶丄敀愇偺悢傪倷乿傕偟偔偼丄乽堏摦偟偨愇偺悢傪倶丄偆偪崟愇傪倷乿偲偍偒丄楢棫曽掱幃傪棫偰偰偔偩偝偭偨曽偼丄俇柤偱偟偨丅
乽堏摦偟偨愇偺屄悢傪倶乿偲偍偄偨曽偑俉柤丄乽堏摦偟偨敀愇偺悢傪倶乿偲偍偄偰丄曽掱幃傪棫偰偰偔偩偝偭偨曽偑侾侽柤偱偟偨丅
堏摦偟偨敀愇偺屄悢傪倶偲偍偔偲丄堏摦偟偨崟愇偺屄悢偼俋倶偲側傝傑偡丅側偤側傜丄敔俛偺拞偵偁傞崟愇偺妱崌偑曄壔偟偰偄側偄偐傜偱偡丅曄悢偺抲偒曽偵傛偭偰丄棫偰傞幃偺暋嶨偝偑寉尭偱偒傑偡偹丅
曽掱幃傪巊傢偢偵夝偄偰偔偩偝偭偨曽傕偄傜偭偟傖偄傑偟偨丅 nao偝傫丄抴鍋偺憙忛偝傫偺傛偆偵丄 帇妎揑偵丄柺愊偱峫偊傞偲丄曽掱幃傪抦傜側偄彫妛惗偵傕愢柧偱偒傑偡偹丅

 E-mail
E-mail
 top
top