侾侽侽丏嶰妏宍偺柺愊
惓嶰妏宍傪侾侽屄壓恾偺傛偆偵暲傋偰暯峴巐曈宍俙俛俠俢傪嶌傞丅 偙偺暯峴巐曈宍傪峔惉偟偰偄傞惓嶰妏宍偼丄懳妏宍俛俢偵傛偭偰偄偔偮偐偺嶰妏宍偵暘偐傟傞丅 偙偺偲偒丄師偺栤偄偵摎偊側偝偄丅
乮侾乯恾偺俤丄俥偵懳偟丄慄暘偺斾俙俥丗俥俤傪媮傔傛丅
乮俀乯恾偺奃怓晹暘偺柺愊偺榓偼丄暯峴巐曈宍偺柺愊偺壗暘偺偄偔偮偱偡偐丅
Weekend Mathematics乛栤戣乛栤戣100
侾侽侽丏嶰妏宍偺柺愊
惓嶰妏宍傪侾侽屄壓恾偺傛偆偵暲傋偰暯峴巐曈宍俙俛俠俢傪嶌傞丅 偙偺暯峴巐曈宍傪峔惉偟偰偄傞惓嶰妏宍偼丄懳妏宍俛俢偵傛偭偰偄偔偮偐偺嶰妏宍偵暘偐傟傞丅 偙偺偲偒丄師偺栤偄偵摎偊側偝偄丅
乮侾乯恾偺俤丄俥偵懳偟丄慄暘偺斾俙俥丗俥俤傪媮傔傛丅
乮俀乯恾偺奃怓晹暘偺柺愊偺榓偼丄暯峴巐曈宍偺柺愊偺壗暘偺偄偔偮偱偡偐丅
戝恖偺偨傔偺嶼悢楙廗挔
嵅摗峆梇
島択幮僽儖乕僶僢僋僗
夝摎丒偦偺1
乮儁儞僱亅儉丗昹揷丂柧枻乯
恾宍栤戣側偺偱丆倁俛偱夝偒傑偟偨丏岺晇偟偰嶌偭偨僾儘僌儔儉偱偼側偄偺偱丆抪偢偐偟偄偺偱偡偑丆媮愊栤戣偱偼巇曽偁傝傑偣傫丏僿儘儞偺岞幃傪巊梡偟偨傕偺偲丆愊暘寁嶼偺椉曽偺夝朄偱夝偄偰傒傑偟偨丏
俙俥乛俥俤亖俆丆柺愊斾偼侾侾乛俁侽偱偡丏
Option Explicit Sub Form_Load() Picture1.Scale (-0.5, 3.75)-(6, -2.75) Picture1.BackColor = vbWhite Picture2.BackColor = vbWhite Picture2.Picture = LoadPicture("gazou100a.gif") Picture3.BackColor = vbWhite Picture4.BackColor = vbWhite End Sub Sub Command1_Click() Dim x(20) As Double Dim y(20) As Double Dim a As Double Dim b As Double Dim c As Double Dim d As Double Dim kotae1 As Double Dim kotae2 As Double Dim zentai As Double Dim j As Integer Dim jj As Integer Dim jjj As Integer ' For j = 0 To 10 Step 2 x(j) = j * 0.5 y(j) = 0 Next j x(1) = 0.5 y(1) = Sqr(3) * 0.5 For j = 3 To 11 Step 2 x(j) = x(j - 2) + 1 y(j) = y(1) Next j 'BD:y=(Dy-By)/(Dx-Bx)*(x-Bx)+By=(y(11)-y(0))/(x(11)-x(0))*(x-x(0))+y(0)=a*x+b a = (y(11) - y(0)) / (x(11) - x(0)) b = a * (-x(0)) + y(0) For j = 1 To 9 'y=(y(j+1)-y(j))/(x(j+1)-x(j))*(x-x(j))+y(j)=c*x+d c = (y(j + 1) - y(j)) / (x(j + 1) - x(j)) d = c * (-x(j)) + y(j) 'y=a*x+b=c*x+d x(j + 11) = (d - b) / (a - c) y(j + 11) = a * x(j + 11) + b Next j Picture1.Cls Picture1.Line (x(1), y(1))-(x(0), y(0)), vbBlack Picture1.Line -(x(10), y(10)), vbBlack Picture1.Line -(x(11), y(11)), vbBlack For j = 1 To 10 Picture1.Line -(x(j), y(j)), vbBlack Next j Picture1.Line (x(0), y(0))-(x(11), y(11)), vbBlack Picture1.CurrentX = x(1) Picture1.CurrentY = y(1) Picture1.Print "A" Picture1.CurrentX = x(0) Picture1.CurrentY = y(0) Picture1.Print "B" Picture1.CurrentX = x(10) Picture1.CurrentY = y(10) Picture1.Print "C" Picture1.CurrentX = x(11) Picture1.CurrentY = y(11) Picture1.Print "D" Picture1.CurrentX = x(2) Picture1.CurrentY = y(2) Picture1.Print "E" Picture1.CurrentX = x(12) Picture1.CurrentY = y(12) Picture1.Print "F" ' kotae1 = nagasa(1, 12, x(), y()) / nagasa(2, 12, x(), y()) zentai = Sqr(3) * 0.25 * 1 * 1 * 10 kotae2 = 0 For j = 1 To 10 jj = -(j > 1) * (j + 10) jjj = (j Mod 10) + 11 kotae2 = kotae2 + menseki(j, jj, jjj, x(), y()) Next j kotae2 = kotae2 / zentai Picture3.Cls Picture3.Print "AF/FE="; kotae1; ", 柺愊斾="; kotae2; Picture3.Print "="; bunsuu(kotae2); " (僿儘儞偺岞幃巊梡)" ' Dim xx As Double Dim y1 As Double Dim y2 As Double Dim kizami As Double kizami = 0.000002 '******** kotae2 = 0 Picture4.Cls For j = 1 To 9 Step 2 For xx = x(-(j > 1) * (j + 10)) + kizami * 0.5 To x(j) Step kizami y1 = a * xx + b y2 = (y(j) - y(j - 1)) / (x(j) - x(j - 1)) * (xx - x(j - 1)) + y(j - 1) kotae2 = kotae2 + (y2 - y1) * kizami Picture1.Line (xx, y1)-(xx, y2), vbGreen Next xx For xx = x(j) + kizami * 0.5 To x(j + 11) Step kizami y1 = a * xx + b y2 = (y(j + 1) - y(j)) / (x(j + 1) - x(j)) * (xx - x(j)) + y(j) kotae2 = kotae2 + (y2 - y1) * kizami Picture1.Line (xx, y1)-(xx, y2), vbGreen Next xx For xx = x(j + 11) + kizami * 0.5 To x(j + 1) Step kizami y1 = (y(j + 1) - y(j)) / (x(j + 1) - x(j)) * (xx - x(j)) + y(j) y2 = a * xx + b kotae2 = kotae2 + (y2 - y1) * kizami Picture1.Line (xx, y1)-(xx, y2), vbGreen Next xx For xx = x(j + 1) + kizami * 0.5 To x(-(j < 9) * (j + 12) - (j = 9) * 11) Step kizami y1 = (y(j + 2) - y(j + 1)) / (x(j + 2) - x(j + 1)) * (xx - x(j + 1)) + y(j + 1) y2 = a * xx + b kotae2 = kotae2 + (y2 - y1) * kizami Picture1.Line (xx, y1)-(xx, y2), vbGreen Next xx Picture4.Cls Picture4.Print "柺愊斾="; kotae2 / zentai; "(愊暘巊梡)" Next j Picture1.Line (x(1), y(1))-(x(0), y(0)), vbBlack Picture1.Line -(x(10), y(10)), vbBlack Picture1.Line -(x(11), y(11)), vbBlack For j = 1 To 10 Picture1.Line -(x(j), y(j)), vbBlack Next j Picture1.Line (x(0), y(0))-(x(11), y(11)), vbBlack Picture1.CurrentX = x(1) Picture1.CurrentY = y(1) Picture1.Print "A" Picture1.CurrentX = x(0) Picture1.CurrentY = y(0) Picture1.Print "B" Picture1.CurrentX = x(10) Picture1.CurrentY = y(10) Picture1.Print "C" Picture1.CurrentX = x(11) Picture1.CurrentY = y(11) Picture1.Print "D" Picture1.CurrentX = x(2) Picture1.CurrentY = y(2) Picture1.Print "E" Picture1.CurrentX = x(12) Picture1.CurrentY = y(12) Picture1.Print "F" End Sub Sub Command2_Click() Unload Me End Sub Private Function nagasa(ByVal a As Integer, ByVal b As Integer, ByRef x() As Double, ByRef y() As Double) As Double nagasa = Sqr((x(b) - x(a)) * (x(b) - x(a)) + (y(b) - y(a)) * (y(b) - y(a))) End Function Private Function menseki(ByVal a As Integer, ByVal b As Integer, ByVal c As Integer, ByRef x() As Double, ByRef y() As Double) As Double Dim xx(2) As Double Dim yy(2) As Double Dim hen(2) As Double Dim s As Double Dim j As Integer Dim jj As Integer xx(0) = x(a) yy(0) = y(a) xx(1) = x(b) yy(1) = y(b) xx(2) = x(c) yy(2) = y(c) s = 0 For j = 0 To 2 jj = (j + 1) Mod 3 hen(j) = nagasa(j, jj, xx(), yy()) s = s + hen(j) Next j s = s * 0.5 menseki = s For j = 0 To 2 menseki = menseki * (s - hen(j)) Next j menseki = Sqr(menseki) End Function Private Function GCM(ByVal a As Integer, ByVal b As Integer) As Integer If b = 0 Then GCM = a Else GCM = GCM(b, a Mod b) End If End Function Private Function bunsuu(ByVal x As Double) As String Dim n As Integer Dim sa As Double Dim min As Double Dim bumbo As Integer Dim bunshi As Integer min = 10000 '******** If Int(x) = x Then bunsuu = Str(x) Else n = Int(x) x = x - n For bumbo = 2 To 1000 '******** For bunshi = 1 To bumbo - 1 If GCM(bumbo, bunshi) = 1 Then sa = Abs(x - bunshi / bumbo) If min > sa Then min = sa bunsuu = Str(n * bumbo + bunshi) + "/" + Str(bumbo) End If End If Next bunshi Next bumbo End If End Function
夝摎丒偦偺2
乮儁儞僱亅儉丗偪偐傂偱乯
乮侾乯俛傪尨揰偲偟俛俠傪倶幉偲偡傞捈峴嵗昗偵偍偄偰丆俙俤 傪捠傞捈慄 倷1丆俛俥俢傪捠傞捈慄 倷2偺幃傪媮傔丆楢棫曽掱 幃偲偟偰夝偄偰俥偺嵗昗傪媮傔傞丅俙偲俤偺倶嵗昗偼帺柧偱偁 傞偐傜丆俥偺倶嵗昗偲偺嵎傪媮傔傟偽摎傪摼傞丅堦曈偺挿偝侾偺惓嶰妏宍傪峫偊傞偲丆
丂丂丂倷1亖亅俀併俁倶亄俀併俁
丂丂丂倷2亖併俁倶乛乮俆亄侽丏俆乯
偙傟傪夝偔偲倶亖11/12傪摼傞丅廬偭偰
丂丂丂俙俥乛俥俤亖乮11-6乯乛乮12-11乯亖俆乛侾
丂丂丂亪俙俥丗俥俤亖俆丗侾
乲暿夝乴俙俤偺挿偝傪俇偲偍偔偲丆俥俤偵懳墳偡傞奺幬曈偺挿 偝偼俛仺俤仺丒丒丒仺俠偵偍偄偰
丂丂丂侽丗1/6丗2/6丗3/6丗4/6丗5/6乮丗6/6乯
偲捈慄揑偵曄壔偡傞丅
丂丂丂亪俙俥丗俥俤亖俆丗侾
乮俀乯夝摎丂丗丂(奃怓)乛(慡柺愊乯亖侾侾乛俁侽
丂惓嶰妏宍偺奺幬曈侾侾屄偲捈慄俙俢傪昞偡幃寁侾俀屄傪(侾) 摨條捈岎嵗昗忋偱媮傔丆嶰妏宍偺奺幬曈偲捈慄俙俢偲偺岎揰乮ex.F 乯偺嵗昗傪楢棫曽掱幃偵傛傝媮傔傞丅偙傟傜偺嵗昗傪巊偭偰捈 慄俙俢傛傝壓偺敀怓晹暘偺柺愊傪媮傔丆偦偺崌寁偺俀攞傪慡柺 愊偲斾妑偟偨丅
寁嶼偺徻嵶偼(侾)偲摨條偱偡偑斚嶨偵側傞偺偱徣棯偟傑偡丅
丂側偍丆捈姶揑曽朄偑側偄偐偲悘暘扵偟傑偟偨偑尒偮偐傝傑偣傫偱偟偨丅
夝摎丒偦偺3
乮儁儞僱亅儉丗俰俽儈儖乯
栤偄1
恾偺傛偆偵揰俛傪揰O偲偟偰XY嵗昗傪峫偊丆惓嶰妏宍偺堦曈偺挿偝傪2偲偡傞偲丆
嵗昗偼揰A乮1丆併3乯丆C乮3丆併3乯丆I乮5丆併3乯丆M乮7丆併3乯S乮9丆併3乯 V(11丆併3)丆E(2丆0)丒丒丒丒丒U乮10丆0乯偲側傞丏
慄暘BV偼y=併3乛11丒x
慄暘AE偼倷=-併3丒x+2併3丂丂偟偨偑偭偰慄暘BV偲慄暘AE偺岎揰偺嵗昗F偼乮11乛4丆併3乛4乯
偙偺帪丆A俥偲FE偺挿偝偼偦傟偧傟5乛3丆1乛3偲側傝丆偦偺斾偼5丗1
栤偄2
偦傟偧傟偺嶰妏宍偼偡傋偰憡帡偱偁傞偙偲傛傝丆慄暘AB偺挿偝傪1偲偡傞偲
丂丂丂AF亖5乛6丆FE亖1乛6丆DE亖1乛5丆DC亖4乛5丆CG亖4乛6丆GH亖2乛6丆HJ亖2乛5丆JI亖3乛5丆IK亖1乛2
丂廬偭偰丆嶰妏宍ABE偺柺愊傪俽偲偡傞偲丆
丂惵偺晹暘偺柺愊
亖乷俽亄乮4乛5乯2亊俽亄乮3乛5乯2亊俽亄乮2乛5乯2亊俽亄乮1乛5乯2亊俽乸亊2
亖22俽乛5
堦曽丆暯峴巐曈宍偺柺愊偼10亊俽亊6乛5亖60俽乛5
廬偭偰偦偺斾偼丂22乛60亖11乛30
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂摎偊丂11乛30
夝摎丒偦偺4
乮儁儞僱亅儉丗岼偺柌乯
丂恾偺嵍偐傜3屄栚偺嶰妏宍偲懳妏慄BD偺岎揰傪G偲偡傞偲丄仮BCD偲仮BEG偼憡帡斾俆丗侾偺憡帡嶰妏宍偱偁傞偐傜AB偲EG偺斾偼俆丗侾偱偁傞丅場偭偰AF偲FE偺斾偼俆丗侾偲側傞丅
丂枖丄奃怓偺嶰妏宍偼慡偰憡帡偱摨偠柺愊偺傕偺偑擇偮偯偮懚嵼偡傞丅堦斣彫偝側嶰妏宍偲弴師戝偒偔側傞嶰妏宍偺憡帡斾偼侾丗俀丗俁丗係丗俆偱偁傞丅場偭偰柺愊斾偼侾丗係丗俋丗侾俇丗俀俆偲側傞丅崱斾侾偺柺愊傪倱偲偡傞偲奃怓晹偺柺愊偺憤榓偼侾侾侽倱偲側傞丅偲偙傠偱惓嶰妏宍堦屄偺柺愊傪S偲偡傞偲仮ABF偺柺愊偼5/俇攞偱偁傞偐傜愭掱偺斾傪崌寁偟偨傕偺偺俀攞偱偁傞侾侾侽偼侾侾俽/俁偲側傞丅偙偙偱暯峴巐曈宍偺柺愊偼惓嶰妏宍侾侽屄暘側偺偱侾侽S偱偁傞丅場偭偰奃怓晹偺柺愊偼乮侾侾俽/俁乯/侾侽S亖侾侾/俁侽偲側傞丅
丂埲忋傛傝媮傔傞傕偺偼
丂乮侾乯俆丗侾
丂乮俀乯侾侾/俁侽丂
夝摎丒偦偺5
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
乮侾乯俙俥丗俥俤亖俆丗侾偱偡丅
乮俀乯侾侾乛俁侽偱偡丅
乮侾乯傪峫偊傞偲偒丄嵍懁偵傕偆侾偮嶰妏宍傪捛壛偡傞偲傢偐傝傗偡偔側傝傑偡丅
俇偮偺仮俢俷俛丄仮俢俙俥丄仮俢俵俶丄仮俢俲俴丄仮俢俬俰丄仮俢俧俫偼憡帡偱偡丅
憡帡斾偼丄俇丗俆丗係丗俁丗俀丗侾偱偡丅
偩偐傜丄傕偲偺惓嶰妏宍偺侾曈傪俇偲偡傟偽丄俙俥亖俆丄俥俤亖侾偲側傝傑偡丅
乮俀乯乮侾乯傛傝俙俥亖俆丄俵俶亖係丆俲俴亖俁丄俬俰亖俀丄俧俫亖侾偱偡丅
仮俙俛俥丄仮俵俽俶丄仮俲俼俴丄仮俬俻俰丄仮俧俹俫偼憡帡偱偡丅
傕偲偺惓嶰妏宍偺柺愊傪俁侽偲偟偰傒傞偲丄仮俙俛俥亖俁侽亊俆乛俇亖俀俆亖俆2丄
仮俵俽俶亖係2亖侾俇丄仮俲俼俴亖俁2亖俋丄仮俬俻俰亖俀2丄仮俧俹俫亖侾2亖侾丅
慄暘俛俢偺忋偲壓偲偱偼揰俴偵娭偟偰懳徧側偺偱丄
乮俀俆亄侾俇亄俋亄係亄侾乯乛乮俁侽亊俆乯亖俆俆乛侾俆侽亖侾侾乛俁侽
偲側傝傑偡丅
夝摎丒偦偺6
乮儁儞僱亅儉丗棨墱榁恖乯
(1)AF:FE=5:1
(2)AF:FE=5:1側偺偱丄FE傪堦曈偵傕塭偺偮偄偨嶰妏宍偺柺愊偼惓嶰妏宍偺柺愊傪侾偲偟偰丄 1/6*1/5(掙曈偑1/5丄崅偝偑1/6丅偳偪傜偱傕偄偄偱偡偑乯丅
偦偺塃墶偺彫偝偄暯峴巐曈宍偺拞偺塭偺偮偄偨彫偝偄曽偺嶰妏宍偺柺愊偼2/5*2/6...丅
乮1/6*1/5+2/6*2/5+3/6*3/5....+5/6*5/5))丅
摨偠傕偺偑俀偮偯偮丗2*(1/6*1/5+2/6*2/5+3/6*3/5....)丅
暯峴巐曈宍偺柺愊偼10
偲偄偆偙偲偱丄2*(1/6*1/5+2/6*2/5+3/6*3/5....)/10=2*(1+4+9+16+25)/(5*6*10)=11/30
夝摎丒偦偺7
乮儁儞僱亅儉丗儈儖僋乯
(1)CD傪曈偲偡傞丄婛偵偁傞恾宍偲廳側傜側偄傛偆側惓嶰妏宍CDG傪昤偔丅仮BEF佷仮 BGD傛傝丄EF=(1/6)DG=(1/6)AE=(1/5)AF丅傛偭偰丄AF:FE=5:1
(2)(1)偺傛偆偵憡帡傪峫偊傞偙偲偵傛傝丄5偮偺奃怓晹暘偺嶰妏宍偼憡帡斾1:2:3:4:5丅
堦斣偱偐偄搝偼暯峴巐曈宍偺1/10亊5/6=1/12丅堦斣彫偝偄傕偺偼1/12亊1/25=1/300丅
媮傔傞柺愊偼丄
丂丂1/300亊(12+22+32+42+52)亊2=11/30
夝摎丒偦偺8
乮儁儞僱亅儉丗Toru乯
奃怓晹暘偼侾侽屄偺嶰妏宍偐傜側傝丄偦傟偧傟憡帡偱 憡帡斾偼侾丗俀丗俁丗係丗俆乮崌摨偺傕偺偑俀偮偢偮乯
乮侾乯 AF丗FE偼堦斣戝偒偄傕偺偲堦斣彫偝偄傕偺偺憡帡斾偱俆丗侾
乮俀乯 憡帡斾侾丗俀丗俁丗係丗俆傛傝柺愊斾偼侾丗係丗俋丗侾俇丗俀俆丄
傛偭偰堦斣彫偝偄嶰妏宍偺柺愊傪侾偲偟偰奃怓偺晹暘偺柺愊偺榓偼丄
乮侾亄係亄俋亄侾俇亄俀俆乯亊俀亖侾侾侽
惓嶰妏宍ABE偺柺愊偼乮侾乯傛傝俀俆亊俇乛俆亖俁侽
傛偭偰丄暯峴巐曈宍ABCD偺柺愊偼俁侽亊侾侽亖俁侽侽
傛偭偰媮傔傞摎偼丂侾侾侽乛俁侽侽亖侾侾乛俁侽
夝摎丒偦偺9
乮儁儞僱亅儉丗暷傐傫乯
乮侾乯忋婰偺傛偆偵捈慄俛俠偐傜墑挿偟偨捈慄偲丆慄暘俙俛偲暯峴偵俢偐傜堷偄偨捈慄偺岎揰傪俧偲偡傞丅
仮俛俤俥佷仮俛俧俢偱丆憡帡斾偼1丗6
傑偨丆忦審傛傝俙俤亖俢俧
亪俙俥丗俥俤亖5丗1
乮俀乯揰俫傪忋婰偺傛偆偵抲偔
乮侾乯傛傝嶰妏宍嘍乫偲嶰妏宍嘆偺憡帡斾偼5丗1
嘍乫偲嘆偺柺愊斾偼丆25丗1
嶰妏宍嘆乣嘍丆嶰妏宍嘆乫乣嘍乫偼偡傋偰憡帡
憡帡斾偼丆
嘆丗嘇丗嘊丗嘋丗嘍亖1丗2丗3丗4丗5
柺愊斾偼
嘆丗嘇丗嘊丗嘋丗嘍亖1丗4丗9丗16丗25
傑偨丆嘆亖嘆乫丆嘇亖嘇乫丆嘊亖嘊乫丆嘋亖嘋乫丆嘍亖嘍乫
偙偙偱仮嘆偲暯峴巐曈宍俙俛俠俢偺柺愊斾傪媮傔傞丅
憡帡斾仮俛俤俫丗仮俛俠俢亖1丗5
柺愊斾仮俛俤俫丗仮俛俠俢亖1丗25
傑偨丆BF丗俥俫亖5丗1傛傝
柺愊斾仮俛俤俥丗仮俥俤俫亖5丗1
柺愊斾仮俛俤俫丗仮俥俤俫亖6丗1
傛偭偰丆柺愊斾仮俛俠俢丗仮俥俤俫亖150丗1
暯峴巐曈宍俙俛俠俢丗仮俥俤俫亖300丗1
奃怓偺晹暘偺柺愊偺榓丗偼丆乮嘆亄嘇亄嘊亄嘋亄嘍乯亊2側偺偱丆 偙傟傜偵傛傝丆
暯峴巐曈宍俙俛俠俢丗奃怓偺晹暘偺柺愊偺榓亖300丗乮1+4+9+16+25乯亊2亖300丗110
丂丂丂丂摎偊丗11/30
夝摎丒偦偺10
乮儁儞僱亅儉丗嵅栰堯怣乯
忋恾偺傛偆偵丄揰俧丄俫丄俬丄俰丄俲丄俴丄俵丄俶丄俷丄俹丄俻丄俼丄俽丄俿丄倀偲偍偔丅 (1)壓恾偺傛偆偵丄惓嶰妏宍俢俠倁傪暯峴巐曈宍俙俛俠俢偵晅偗壛偊傞丅
俥俤乂俢倁傛傝
丂丂丂俥俤丗俢倁亖俛俤丗俛倁亖侾丗俇
丂丂丂亪丂丂俢倁亖俇俥俤丂丂丒丒丒(1)
俢倁亖俙俤傛傝
丂丂丂俙俤亖俇俥俤丂丂丒丒丒(2)
丂丂丂亪丂俙俥亖俙俤亅俥俤
丂丂丂丂丂丂丂亖俇俥俤亅俥俤(丂(2)傛傝)
丂丂丂丂丂丂丂亖俆俥俤丂丂丒丒丒(3)
丂丂丂亪丂俙俥丗俥俤亖俆俥俤丗俥俤亖俆丗侾丂丂丒丒丒(摎)
俥俤乂俬俰傛傝
丂丂丂俥俤丗俬俰亖俛俤丗俛俰亖侾丗俀
丂丂丂亪丂俬俰亖俀俥俤丂丂丒丒丒(4)
偝傜偵丄
俬俰 亖俀俥俤(佹(4)傛傝) 亖俀亊(1/6)俙俤(佹(2)傛傝) 亖(1/3)俫俰(佹俙俤亖俫俰)丂丂丒丒丒(5)
亪俫俬 亖俫俰亅俬俰 亖(2/3)俫俰(佹(5)傛傝) 亖係俥俤(佹(5)傛傝)丂丂丒丒丒(6)
俥俤乂俵俶傛傝
丂丂丂俥俤丗俵俶亖俛俤丗俛俶亖侾丗俁
丂丂丂亪丂俵俶亖俁俥俤丂丂丒丒丒(7)
偝傜偵丄
俵俶 亖俁俥俤(佹(7)傛傝) 亖俁亊(1/6)俙俤(佹(2)傛傝) 亖(1/2)俴俶(佹俙俤亖俴俶)丂丂丒丒丒(8)
亪俴俵 亖俴俶亅俵俶 亖(1/2)俴俶(佹(8)傛傝) 亖俁俥俤(佹(8)傛傝)丂丂丒丒丒(9)
懳徧惈傛傝丄
丂丂丂仮俠俢倀佭仮俙俛俥丂丂丒丒丒(10)
丂丂丂仮俿俽倀佭仮俤俧俥丂丂丒丒丒(11)
丂丂丂仮俼俽俻佭仮俫俧俬丂丂丒丒丒(12)
丂丂丂仮俹俷俻佭仮俰俲俬丂丂丒丒丒(13)
丂丂丂仮俶俷俵佭仮俴俲俵丂丂丒丒丒(14)
丂丂丂丂丂丂丂丂
忋恾偺幬慄晹暘偺柺愊偺榓傪俽偲偍偔偲丄
俽 亖仮俙俛俥亄仮俤俧俥亄仮俫俧俬亄仮俰俲俬亄仮俴俲俵 丂丂亄仮俶俷俵亄仮俹俷俻亄仮俼俽俻亄仮俿俽倀亄仮俠俢倀 亖俀(仮俙俛俥亄仮俤俧俥亄仮俫俧俬亄仮俰俲俬亄仮俴俲俵)丂丂丒丒丒(15)
丂丂丂丂(佹(10),(11),(12),(13),(14)傛傝)
俙俛乂俫俤乂俴俰乂俹俶乂俿俼乂俢俠丂偐偮丂俙俤乂俫俰乂俴俶乂俹俼乂俿俠傛傝
丂丂丂仮俙俛俥佷仮俤俧俥佷仮俫俧俬佷仮俰俲俬佷仮俴俲俵丂丂丒丒丒(16)
仮俙俛俥丗仮俤俧俥 亖俙俥2丗俤俥2(佹(16)傛傝) 亖俀俆俥俤2丗俤俥2(佹(3)傛傝) 亖俀俆丗侾
丂丂丂亪丂仮俙俛俥亖俀俆仮俤俧俥丂丂丒丒丒(17)
仮俫俧俬丗仮俤俧俥 亖俫俬2丗俤俥2(佹(16)傛傝) 亖侾俇俥俤2丗俤俥2(佹(6)傛傝) 亖侾俇丗侾
丂丂丂亪丂仮俫俧俬亖侾俇仮俤俧俥丂丂丒丒丒(18)
仮俰俲俬丗仮俤俧俥 亖俰俬2丗俤俥2(佹(16)傛傝) 亖係俥俤2丗俤俥2(佹(4)傛傝) 亖係丗侾
丂丂丂亪丂仮俰俲俬亖係仮俤俧俥丂丂丒丒丒(19)
仮俴俲俵丗仮俤俧俥 亖俴俵2丗俤俥2(佹(16)傛傝) 亖俋俥俤2丗俤俥2(佹(9)傛傝) 亖俋丗侾
丂丂丂亪丂仮俴俲俵亖俋仮俤俧俥丂丂丒丒丒(20)
(15)偵丄(17),(18),(19),(20)傪戙擖偡傞偲丄
俽 亖俀(俀俆亄侾亄侾俇亄係亄俋)仮俤俧俥 亖侾侾侽仮俤俧俥 亖侾侾侽亊(1/25)仮俙俛俥(佹(17)傛傝) 亖(22/5)仮俙俛俥丂丂丒丒丒(21)
俙俥丗俥俤亖俆丗侾傛傝
仮俙俛俤丗仮俙俛俥 亖俙俤丗俙俥 亖俇丗俆
丂丂丂亪丂仮俙俛俥亖(5/6)仮俙俛俤丂丂丒丒丒(22)
(22)傪(21)偵戙擖偡傞偲
俽 亖(22/5)亊(5/6)仮俙俛俤 亖(11/3)仮俙俛俤丂丂丒丒丒(23)
暯峴巐曈宍俙俛俠俢亖侾侽仮俙俛俤傛傝
俽 亖(11/3)亊(1/10)暯峴巐曈宍俙俛俠俢(佹(23)傛傝) 亖(11/30)暯峴巐曈宍俙俛俠俢丂丂丒丒丒(24)
廬偭偰丄恾偺幬慄晹暘偺柺愊偺榓偼丄暯峴巐曈宍俙俛俠俢偺柺愊偺(11/30)偱偁傞丅丂丂丒丒丒(摎)
夝摎丒偦偺11
乮儁儞僱亅儉丗Mr.X乯
懳妏慄俛俢偵娭偟偰俙偺懁偵偁傞俆屄偺奃怓偺嶰妏宍偼 憡帡偱偁傝憡帡斾偼嵍偐傜 5:4:3:2:1
懳妏慄俛俢偵娭偟偰俠偺懁偵偁傞俆屄偺奃怓偺嶰妏宍偼 塃偐傜弴偵偙傟傜偺嶰妏宍偵偦傟偧傟崌摨偱偁傞丅
偟偨偑偭偰
乮侾乯AF:FE=俆丗侾
乮俀乯惓嶰妏宍侾偮暘偺柺愊傪俁侽偲偡傞丅
懳妏慄俛俢偵娭偟偰俙偺懁偵偁傞俆屄偺奃怓偺嶰妏宍偺 柺愊偺榓偼 25+16+9+4+1=55
暯峴巐曈宍偺柺愊偺 俀亊俆俆/俁侽侽亖侾侾/俁侽 偵偁偨傝傑偡丅
丂夝摎丒偦偺12
乮儁儞僱亅儉丗撪奀丂堢乯
(1) AF丗FE=俆丗侾
(2) 11/30
乮夁掱乯
AD忋偺嶰妏宍偺捀揰傪(A)丆G丆H丆I丆J丆(D)
BD忋偺嶰妏宍偺捀揰傪(B)丆(F)丆K丆L丆M丆N丆O丆P丆Q丆R丆(D)偲偟傑偡丅
(1)丂CD/EK=BC/BE=5
丂嚈ABF佷 嚈EKF 亪AF/FE=AB/EK=CD/EK=5
(2)嚈ABF/嚈ABE=AF/AE=AF/(AF+FE)=5/6丂亪嚈ABF=(5/6)嚈ABE=(1/12)仩ABCD
丂嚈GKL丒嚈HMN丒嚈IOP丒嚈JQR偼嚈ABF偲憡帡丅
憡帡斾偼偦傟偧傟嚈ABF偺4/5丒3/5丒2/5丒1/5偱丄柺愊斾偼偦偺俀忔丅
丂傛偭偰丄媮傔傞柺愊
=2*(嚈ABF+嚈GKL+嚈HMN+嚈IOP+嚈JQR)
=2嚈ABF*(1+16/25+9/25+4/25+1/25)
=(22/5)嚈ABF=(11/30)仩ABCD
夝摎丒偦偺13
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
栤戣侾丏慄暘偺斾偼AF丗FE=俆丗侾偱偁傞
栤戣俀丏奃怓偲敀怓偺柺愊偺斾偼侾侾乛俁侽偱偡
憡帡宍偺柺愊斾偼侾曈亊侾曈丗侾曈亊侾曈偵側傝傑偡
廬偭偰SI丗S5亖俆亊俆丗侾亊侾偱偡
嵍偺忋偐傜塃傊S1丄S2丄S3丄S4丄S5丄嵍偺壓丄塃傊S6丄S7丄S8丄S9丄S10丄
恾偼戝偒偄偺偱S3乣S5丄S6乣S10傑偱徣棯偟傑偟偨丅
恾偺懳妏慄偺忋丂仮ABF亖S1丄仮GLN亖S2丄乧
懳妏慄偺壓丂仮FEL亖S10丄仮NHP亖S9丄乧
堦曈傪俇cm偲偟偰峫偊傑偟偨
柺愊S1=25/25亊S1
丂丂S2=16/25亊S1
丂丂S3=9/25亊S1
丂丂S4=4/25亊S1
丂丂S5=2/25亊S1
S1=仮ABE偺柺愊亊俆乛俇
S5=1/25亊仮ABE偺柺愊亖1/30亊仮ABE偺柺愊
S係=係/俁侽亊仮ABE偺柺愊
S俁=俋/俁侽亊仮ABE偺柺愊
S俀=侾俇/俁侽亊仮ABE偺柺愊
S侾=俀俆/俁侽亊仮ABE偺柺愊
奃怓偺柺愊偺崌寁偼
S=2亊乮S1+S2+S3+S4+S5乯=11/3亊仮ABE偺柺愊
暯峴巐曈宍偺柺愊亖侾侽亊仮ABE偺柺愊
暯峴巐曈宍偺柺愊丗奃怓偺柺愊亖侾侽丗侾侾乛俁亖俁侽丗侾侾
廬偭偰奃怓偺柺愊偺榓偼暯峴巐曈宍偺柺愊偺侾侾乛俁侽偲側傝傑偡丅
夝摎丒偦偺14
乮儁儞僱亅儉丗嶰妏掕婯乯
(1) 塃抂偵惓嶰妏宍傪1屄偮偗壛偊偰壓恾偺傛偆偵G傪掕傔傞丅
仮BFE 佷 仮BDG丆BE丗BG亖1丗6丂傛傝丂FE丗DG亖1丗6丂亪 AF丗FE亖5丗1 乧乵摎乶
(2) 壓恾偺傛偆偵H傪掕傔傞偲
仮OEH 佷 仮OCD丆OE丗OC亖1丗5丂傛傝丂EH亖(1/5)CD
惓嶰妏宍偺1曈傪1偲偡傞偲丆 暯峴巐曈宍ABCD亖
恾偺悈怓晹暘偼丆
埲忋傛傝乧乵摎乶
夝摎丒偦偺15
乮儁儞僱亅儉丗偡側憼乯
摎偊
(1)AF:FE=5:1 偱偡丅
(2)偺栤戣偼丄偦傟偧傟偺崟偔揾傝偮傇偝傟偨椬偁偆嶰妏宍偑憡帡偱偁傞偙偲 傪棙梡偟丄憡帡斾偐傜柺愊斾傪偩偟偰寁嶼偟偰偄偔丅 暯峴巐曈宍傪峔惉偡傞惓嶰妏宍偺柺愊傪侾偲偍偔偲丄暯峴巐曈宍偼侾侽丄 偦偺敿暘偼俆偲側傞丅 偦傟傪摜傑偊偰丄堦斣嵍偺揾傝偮傇偝傟偨晹暘偺柺愊偼掙曈偺斾偐傜5/6偲側偭偰 偲側傝偺嶰妏宍偲偺憡帡斾偑5:1偱偁傞偙偲偐傜丄柺愊斾25:1偲側傝丄偦傟傛傝 寁嶼偡傞偲1/30 丅
敿暘壓偵嶰妏宍傪尒偰傒傞偲丄嵍偐傜偦偺憡帡斾偑1:2:3:4:5偵側傞偺偱丄柺愊斾偼 1:4:9:16:25丄偮傑傝1/30偵懳偟偰偦偺柺愊斾偱懚嵼偡傞偺偱
(1/30 + 4/30 + 9/30 + 16/30 + 25/30)亖55/30
忋壓俀偮摨偠傕偺偑偁傞偺偱俀攞偟偰55/15
偙傟傪10偱妱偭偰11/30偑摼傜傟傞丅
夝摎丒偦偺16
乮儁儞僱亅儉丗challenger乯
(1)暯峴慄偲慄暘偺斾偵偍偒偐偊偰峫偊傞偽傛偄偐傜AF:FE=5:1
(2)懳妏慄BD傛傝忋懁偵偁傞5屄偺奃怓晹暘偺嶰妏宍偼屳偄偵憡帡 偱憡帡斾偼5:4:3:2:1偱偁傞偐傜偙傟傜5屄偺柺愊偺榓偼
1+(4/5)2+(3/5)2+(2/5)2+(1/5)2}嚈ABF = (11/5)嚈ABF = (11/5)*(5/6)嚈ABE = (11/6)嚈ABE
偙偙偱丄暯峴巐曈宍偺柺愊傪S偲偡傞偲偡傋偰偺奃怓晹暘偺柺愊偼
(11/6)*2*(1/10)S=(11/30)S
偟偨偑偭偰丄11/30攞偱偁傞丅
夝摎丒偦偺17
乮儁儞僱亅儉丗傗傫傑乯
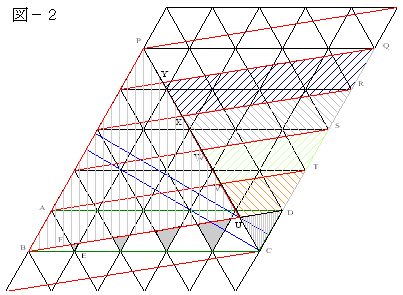
恾亅侾偼暯峴巐曈宍俧俤俫俬丄俬俫俰俲丆俲俰俴俵丄俵俴俠俢傪俛俠偵暯峴偵 俙俛傑偱堏摦偟偨傕偺偱偁傞丅乮嶲峫恾乯
塃偺恾亅俀偼暯峴巐曈宍俙俛俠俢偲懳妏慄俛俢傪忋偵俆偮丄壓偵侾偮暲傋偨傕偺偱偁傞丅
偙偆偡傞偲丄惓嶰妏宍俹俛俠偺堦曈俹俠偼俇摍暘偝傟偰偄傞偙偲偑傢偐傞丅 乮嵟忋晹偲嵟壓晹偺暯峴巐曈宍偼梋暘偩偑摍暘偑尒偨栚偱傢偐傞乯
亪丂俙俥丗俥俤亖俆丗侾
恾亅侾偺奃怓偺嶰妏宍偲恾亅俀偺嶰妏宍俠俢倀丄俠俿倁丄俠俽倂丄俠俼倃丆俠俻倄偼憡帡宍偱偁傞偐傜 嶰妏宍俹俠俻撪偵偱偒傞偙傟傜偺柺愊傪媮傔傟偽傛偄丅
恾偱傢偐傞傛偆偵嶰妏宍俠俢倀偲嶰妏宍俠俿倁偼憡帡偱偁傞丅掙曈偲偡傞晹暘俠俢偲俠俿偼侾丗俀偱偁傞丅 埲壓俠俻倄傑偱弴偵侾丗俁丆侾丗係丆侾丗俆偺憡帡斾偲側傞丅
嵍恾偼惓嶰妏宍傪俀偮暲傋偨傕偺偱偁傞丅 懳妏慄俛俢偵傛偭偰暘偗傜傟偨奃怓晹暘偺柺愊俽俀偼乮嶰妏宍偺堦曈傪俀偲偟偰偍偔乯
摨條偵奃怓晹暘偺柺愊俽係傪媮傔傞偲
摨條偵奃怓晹暘偺柺愊俽俇傪媮傔傞
埲忋偺偙偲偐傜師偺傛偆偵側傞丅
亪丂奃怓晹暘偺柺愊偺榓偲暯峴巐曈宍偺柺愊偺斾偼
栤戣偼俶亖侾侽偱偁傞偐傜
摎偊丂丂(1)丂俆丗侾丂丂丂(2)丂11/30
夝摎丒偦偺18
乮儁儞僱亅儉丗mhayashi乯
(1)
嚈FAD佷嚈FEB 偱憡帡斾偼 AD:EB=5:1 偲暘偐傞偺偱
AF:EF 傕 5:1 偲側傞丏
(2)
奃怓偺侾侽屄偺嶰妏宍偼憡帡側偺偱忋偲摨條側曽朄偱憡帡斾傪弌偟偰偄偔偲弴偵
憡帡斾偼 5:1:4:2:3:3:2:4:1:5 偲側傞丏
傛偭偰柺愊斾偼 25:1:16:4:9:9:4:16:1:25 偲側傞丏
傑偨嚈ABF偼暯峴巐曈宍ABCD偺 (1/10)*(5/6)=1/12 攞丏
(25+1+16+4+9+9+4+16+1+25)*(1/12)*(1/25)=11/30
傛偭偰奃怓偺柺愊偺榓偼暯峴巐曈宍偺柺愊偺俁侽暘偺侾侾偱偁傞丏
惓夝幰
岼偺柌 栭傆偐偟偺偮傜偄偍偠偝傫 棨墱榁恖 儈儖僋 Toru 俰俽儈儖 暷傐傫 嵅栰堯怣 昹揷丂柧枻 Mr.X 撪奀丂堢 忨偺偍偠偝傫 嶰妏掕婯 偡側憼 challenger 偪偐傂偱 傗傫傑 mhayashi
偙偺栤戣偺拞偵偼丄憡帡側娭學偵偁傞嶰妏宍偺慻傒崌傢偣偑偨偔偝傫偁傝傑偡丅 椉僒僀僪偳偪傜偐偵傕偆侾屄嶰妏宍傪晅偗懌偟偰傒傞偲丄傑偨傑偨憡帡側娭學偑昞傟傑偡丅 偦偙偐傜傾僾儘乕僠偟偰偄偔偲夝摎偑尒偊偰偒傑偡偹丅 偨偩偟丄憡帡斾偐傜柺愊斾傪弌偡偲偒偵俀忔偡傞偺傪朰傟側偄偱偔偩偝偄丅

 E-mail
E-mail
 top
top