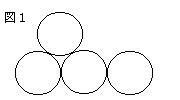
10.1円玉の問題 図1のように、半径1cmの1円玉が4つあります。
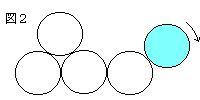
これら4つの1円玉のまわりを図2のように別の1円玉を
滑ることなく転がって1周します。
次の問いに答えてください。 (1)転がった円の中心の描く曲線を書き加えてください。 (2)(1)で書いた曲線の長さはいくらですか。 (3)この時、まわりを回っている1円玉は何回転するでしょうか。
π=3.14とし、答えは四捨五入して少数第1位まで求めてください。
問題の出典
東大寺学園中学校'93入試(1、2のみ)
パズルより面白い中学入試の算数
ピ−タ−・フランクル
講談社
答えと解説
(1)回答
(ペンネ−ム:コレクトコ−ルは106番!)
下の図の赤線が解答である。
半径1cmの1円玉の中心が動くのだから、
それはすなわち図1の全ての1円玉の円周からの距離が1cmの
点の集合を描けばよく、
それは図1の1円玉と同心円である半径2cmの円に他ならない。
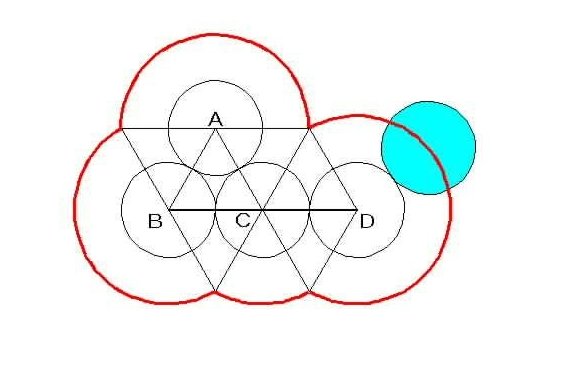
(図の提供:T.N.)
(2)回答
(ペンネ−ム:T.N.)
元の四つの円を中心にした円弧の角度をそれぞれ求める
180+180+60+240=660(度)
軌跡の円弧の半径は2cmなので円弧の長さは
2×3.14×2×(660/360)≒23.0266
Ans. 23.0cm
(2)回答・コメント
図に描かれている三角形がすべて正三角形だということに気づけば、
角度を加算していくのも楽ですね。
(3)回答・その1
(ペンネ−ム:フォルサ ジャポン!!)
1円玉が1回転するとき、中心は2π移動する。
(2)より、中心は22/3・π移動したので、
(22/3・π)/2π=11/3
答え (11/3)回転
(3)回答・その2
(ペンネ−ム:コレクトコ−ルは106番!)
まず、平面上で1円玉を転がしてみる。
直径は2cmとする。
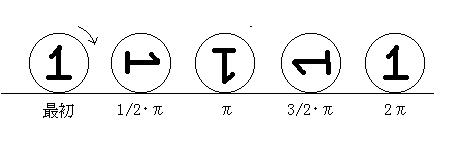
つまり、平面で転がる時は、
円周1周分だけ転がらないと1回転はできない。
ところが、円のまわりを転がるときは、
円周1/2周分で1回転できてしまう。
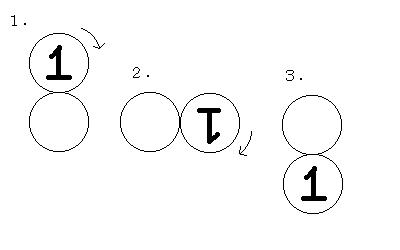
このことは、平面上で転がした時に、
平面が、1円玉と同じペ−スで傾いてあげていることと同じである。
従って、普通に平面で転がる時の1/2の距離で、回転が可能になる。
また、上の図で「基準」のコインから見ると、
1→3で1円玉は180゚移動している。
即ち基準の角度180゚で1回転するはずである。
と、いうことは、前問(2)の「それぞれの大円の弧に対する中心角の合計」
を180゚で割ったものが回転数である。
660/180=3+2/3
従って、1円玉は(3+2/3)回転する。
(3)回答・その3
(ペンネ−ム:T.N.)
同じ直径の円の周りを1回転すると
自転1回転と公転1回転の2回転するため
(660/360)×2=(3−2/3)回転
正解者(ペンネ−ム)
T.N.
フォルサ ジャポン!!
匿名希望
コレクトコ−ルは106番!
es
KEANV REEVESの妻
BABY MINNIE

 戻る
戻る