コロキウム室(源氏香)

第２７回数学的な応募問題

太郎さんは、以前ＮＨＫの「日本の質問」という番組の中で、 この源氏香の話を聞いていました。
香をたいてその香りを鑑賞する遊びを香道と言います。 香道は平安時代、すなわち１０世紀のころからすでに始まっています。 香道と呼ばれるようになったのは室町時代の１５世紀後半で、 江戸時代に入ると芸道として形が整ってきました。
遊びの中で、二組にわかれて同じ種類のものの優劣を競い合う遊びを物合わせというが、 香合わせは物合わせの一つです。

５種類の香を、それぞれの種類ごとに５包ずつ作る。 すなわち、合計２５袋作る。この２５袋の中から５色を選んで。
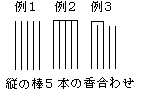
これを順にたく。競技に参加した者は紙に縦の棒５本をたく。 すなわち、例１のように書いておく。
５包の香りを順にかいで（きいて）５種類とも同じなら例２のように横線で引く。
１番目と３番目が同じで、他が違うときは、例の３のようにする。
このように、５種類の香から重複を許して５包の香りを作り、 これをたいて、香りをききわけるとき、一体何通りの違った形を作ることができますか。
これが今回の問題です。できたら、この５本の縦線と横線の違った形を書いてください。
紫式部の「源氏物語」は５４帖あり、この５４帖の一部の題名にこのききわけた香りの記号の名前に あてています。これが源氏香の由来です。

＜補足＞　この源氏香を数学の問題として取り扱ったのは松永良弼（1690頃から1744）である。 松永は関孝和（1640頃〜1708）の孫弟子である。 この源氏香についての解説は、稿本の「断連総術」（1726年）の中に含まれています。

＜出典：数学１００の問題；数学セミナー編集部（日本評論社）＞

香の種類に関係なく形の違いだけを数え上げていけばいいということなので、 以下のように場合分けします。
同じ種類の香がいくつあるかで場合わけです。

香の形	場合の数
５	１
４−１	５Ｃ１＝５
３−２	５Ｃ２＝１０
３−１−１	５Ｃ３＝１０
２−２−１	５Ｃ２×３Ｃ２／２！＝１５
２−１−１−１	５Ｃ２＝１０
１−１−１−１−１	１
合計	５２

＜水の流れ＞さんに届いた質問です。第２７回の応募問題をみて、 NO.604 源氏香についての方法は 知っておいてください。

「今学校で、源氏香についてやってて、それについて各自考えるって問題が出たんですよ だから一応やったんですけど、最後の問いがわかんなくて調べてたときに

（問）源氏香の組み合わせパターンは５２通り。 これは包みを５つ使うからで、包みを増やしたり減らしたりするとパターン数変わる。 包みをｎ個使うときのパターン数をＢ_ｎ通りとしよう。
（１）Ｂ_１Ｂ_２Ｂ_３Ｂ_４を求めよ。
（２）Ｂ_６を求めよ。
（３）実はＢ_１Ｂ_２・・・Ｂ_ｎまでわかるとそこからＢ_ｎ+1が求めることが出来る！ どんな考え方によればいいか。
（４）Ｂ_７〜Ｂ_１０を求めよ。
（５）このＢの意味はなにか(由来）

それで僕はこの（５）がわからないんです。 もしわかるならぜひ教えてもらいたいんですが、お願いします。 （はっきり言ってこんな問題を出す人はそうそういませんね）」