
Weekend Mathematics/コロキウム室/テーマ別/39.お祝い問題・多項式展開係数
| NO.885 | 2000.11.8. | 水の流れ | お祝い問題(1) |
この度のドメイン取得により、新しいホームページのオープン
誠におめでとうございます。これからの貴ページの益々の発展と
管理者のご活躍を心から、お祈りします。
ここで、お祝いの印しに、問題を提供します。
(1+x+x2)nの展開係数をを考えてください。

| NO.887 | 2000.11.9. | Junko | お祝い問題(2) |
試しにいくつか展開してみました。
(1+x+x2)2=x4+2x3+3x2+2x+1
(1+x+x2)3=x6+3x5+6x4+7x3+6x2+3x+1
(1+x+x2)4=
x8+4x7+10x6+16x5+
19x4+16x3+10x2+4x+1
パスカルの三角形を連想しますよね?
同じように係数を並べてみました。
| n | (1+x+x2)nの係数 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | ||||||
| 2 | 1 | 2 | 3 | 2 | 1 | ||||
| 3 | 1 | 3 | 6 | 7 | 6 | 3 | 1 | ||
| 4 | 1 | 4 | 10 | 16 | 19 | 16 | 10 | 4 | 1 |
| ・・・ | ・・・ | ||||||||

| NO.890 | 2000.11.11. | 水の流れ | お祝い問題 (3) |
「お祝いの問題」 で、下記のようなパスカルの三角形みたいのが得られました。 ここで、コロキウムの「コ」と水の流れの「ミ」をとって、コミカルな三角形と呼びましょう。
| n | (1+x+x2)nの係数 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | ||||||
| 2 | 1 | 2 | 3 | 2 | 1 | ||||
| 3 | 1 | 3 | 6 | 7 | 6 | 3 | 1 | ||
| 4 | 1 | 4 | 10 | 16 | 19 | 16 | 10 | 4 | 1 |
| ・・・ | ・・・ | P(n、r) | |||||||
この数字をP(n、r)で表すことにします。
ただし、n=0,1,2,3,・・・・、0≦r≦2n とする。
また、P(n、0)=1、P(n、1)=n、P(n、2nー1)=n、P(n、2n)=1 とする。
すると、このコミカルの三角形は
P(n+1,r)= P(n,r−2)+P(n,r−1)+P(n,r) という性質を持っています。
これは、上の段の3つの和として、順に得られますので、トリボナッチ数列にもなります。

| NO.891 | 2000.11.13. | 水の流れ | 多項式展開係数(1) |
太郎さんは、先日生徒から「ニュートンの2項定理って、何ですか。」と聞かれました。
すぐには答えられませんでしたが、
パスカル(フランス:1623〜1662)の三角形が出てくる2項係数を思い出して、
(a+b)nの2項定理を言いました。ただし、このnは正の整数です。
しかし、ニュートン(イギリス:1642〜1727)と名前が出ているので、
2項定理の発見者はニュートンかしらと疑問に思っていました。そこで、文献で調べてみました。
文学、物理学、気象学の分野で多彩な業績を残したパスカルは、数学においても、
数多くの成果をあげています。転がる円盤の一点が描くサイクロイドの研究はや、
フェルマー(フランス:1601〜1665)と共同で行った確率の研究は、特に優れたものです。
パスカルは確率の研究から、2項式の展開(a+b)nにおいて、
係数の規則性を発見しました。
これが、これがいわゆるパスカルの三角形と言われる魔法の三角形です。
多くの人は、ものご存じですので、割愛します。1654年に発案しました。
実はこの三角形は中国で古くから知られていました。
朱世傑の著書で1303年頃書かれた「四元玉鑑」を見ると、
すでに2項展開したときの係数が書かれています。
これは、高次方程式を解くにあたって使用されていました。
また、ヨーロッパでも16世紀の数学者、カルダノ(イタリア:1501〜1576)らが知っていて、
3次行程式や4次方程式の解法に使ったいました。
弱冠23歳のニューートンが、1665年の初めに、
パスカルの発見した「2項定理」の指数nを拡張して、
正の整数から、負の整数、分数まで拡げ、無限級数にまで発展させている。
αが任意の実数のとき、(1+x)αをベキ級数に展開できる公式を
「ニュートンの2項定理」と言います。
この係数は組み合わせの記号C(n、r)と書きますが、
nが正整数でないと組み合わせの意味がなくなりますが、
n=α,r=nとして、2項係数は、
α(α-1)(α-2)(α-3)・・・(α-n+1)/n!={α,n}と表します。
例えば、α=−1のとき、1+x+x2+x3+x4+・・・+xn+・・・=1/(1−x)
となることです。
で、いろいろと文献を見て、次のような問題を考えてみました。
まず、3項式(1+x+x2)nの展開係数を見て下さい。
n=0,1,2,3,4,5,・・・と展開すると、パスカルの三角形は2項式(1+x)nの展開係数ですが、
似たような奇妙な数列がでてきます。一度見て下さい。
(この三角形をコミカルな三角形と呼びましょう。)
| n | (1+x+x2)nの係数 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | ||||||||
| 2 | 1 | 2 | 3 | 2 | 1 | ||||||
| 3 | 1 | 3 | 6 | 7 | 6 | 3 | 1 | ||||
| 4 | 1 | 4 | 10 | 16 | 19 | 16 | 10 | 4 | 1 | ||
| 5 | 1 | 5 | 15 | 30 | 45 | 51 | 45 | 30 | 15 | 5 | 1 |
| ・・・ | ・・・ | P(n、r) | |||||||||
この数字をP(n、r)で表すことにします。
ただし、n=0,1,2,3,・・・・、0≦r≦2n とする。
また、P(n、0)=1、P(n、1)=n、P(n、2nー1)=n、P(n、2n)=1 とする。
すると、このコミカルの三角形は
P(n+1,r)= P(n,r−2)+P(n,r−1)+P(n,r)
という性質を持っています。
これは、上の段の3つの和として、順に得られますので、トリボナッチ数列にもなります。
ここからが、今回の問題です。次の初項から第k項までの和をkで表してください。
問題1:T1=1+1+1+・・・+T0 (ただし、T0=1とする)
問題2:T2=1+2+3+4+・・・+T1
問題3:T3=1+3+6+10+・・・+T2
問題4:T4=1+4+10+20+・・・+T3
問題5:T5=1+5+15+35+・・・+T4
問題6:一般に、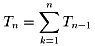
(n=1,2,3,・・・、ただし、T0=1とする)
さて、最後に問題7:
この展開を拡張して、多項式(1+x+x2+x3+x4+・・・)n
の展開係数を考えてください。

| NO.893 | 2000.11.23. | Junko | 多項式展開係数(2) |
この数列は2変数数列(そんな言葉があるのかなあ?)としてとらえなければいけないのかなと思います。
つまり、
問題1:T(1,k)
=T(0,1)+T(0,2)+・・・+T(0,k)
=1+1+1+・・・+T(0,k)
(ただし、任意のkについて、T(0,k)=1とする)
問題2:T(2,k)
=T(1,1)+T(1,2)+・・・+T(1,k)
=1+2+3+4+・・・+T(1,k)
問題3:T(3,k)
=T(2,1)+T(2,2)+・・・+T(2,k)
=1+3+6+10+・・・+T(2,k)
問題4:T(4,k)
=T(3,1)+T(3,2)+・・・+T(3,k)
=1+4+10+20+・・・+T(3,k)
問題5:T(5,k)
=T(4,1)+T(4,2)+・・・+T(4,k)
=1+5+15+35+・・・+T(4,k)
問題6:一般に、
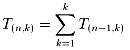
さて改めて、
| 問題1:T(1,k) | =T(0,1)+T(0,2)+・・・+T(0,k) |
| =1+1+1+・・・+T(0,k) | |
| =k |
問題2:
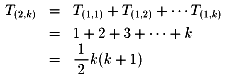
問題3:
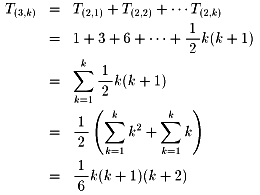
問題4:
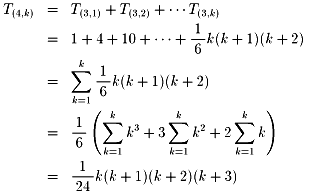
以上のことから、一般に
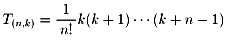
となることが予想されます。

| NO.894 | 2000.11.23. | ねこ | 多項式展開係数(3) |
以下では、Tn=Tn(k)のように書く。
問題1.
T1(k)=1+1+1+1+・・・+1=k
問題2.
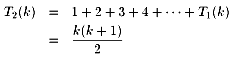
問題3.
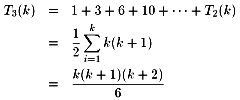
ここで、問題6の解答として次の予想が立つ。
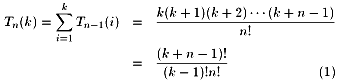
|
(1)が成り立つのを証明する。初めに次の補題を示す。
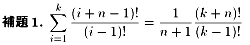
|
証明.帰納法で示す。
i)k=1のとき
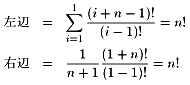
より成立。
ii)k→k+1
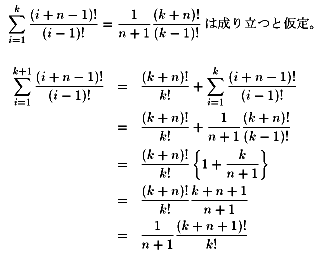
となり成立。
補題1を用いて(1)を証明する。
証明.帰納法で示す。
i)n=1のときは問題1より成立
ii)n→n+1
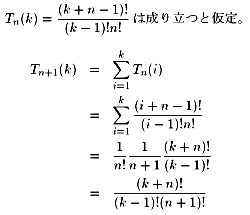
となり、成立。
以上の考察より、以下の解を得る。
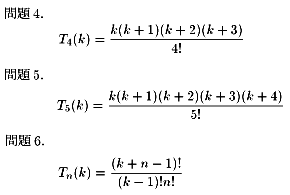
問題7.
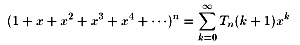
|
証明.帰納法で示す。
i)n=1のとき
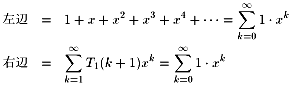
より成立。
ii)n→n+1
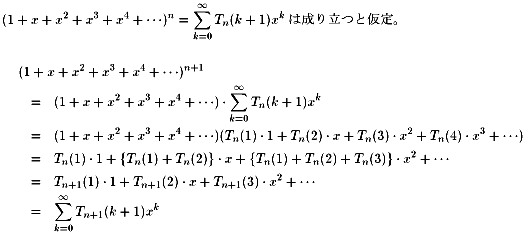
となり、成立。

 戻る
戻る