
Weekend Mathematics/コロキウム室/テーマ別/32.釣り銭の問題・大縄跳び
NO.121 6/19 水の流れ つり銭の問題(1)
生徒が教材費に五百円払う必要があります。
そこに、五百円玉を 持ったn人の生徒と、
千円札しか持っていないn人の合計2n人の
クラス生徒がいます。
担任の私はつり銭を準備していませんでした。
つり銭が不足しないように生徒からもらう方法は
全部で何通りありますか。
ただし、生徒の2n人に区別しないで、
お金の出し方で考えてください。

NO.124 6/21 Junko つり銭の問題(2)
千円札を受け取る前に、
おつりになる五百円玉を持っていればいいのですね。
具体的に数え上げてみることにします。
500円玉をA、千円札をBと表記することにします。

NO.127 7/4 水の流れ つり銭の問題(3)
問題の中で、500円玉を払うのをA,1000円玉を払うのをBとします。 釣り銭がないので、常にaの数がbの数より等しいか大きければよいのです。 これをaを→、bを↑と表せば、→がn個、 ↑ がn個を一列に並べる方法を考えます。
ここで、碁盤の目をした最短経路の問題に変化していきます。
分かり易くするために、求める数をK(n)とすると、
K(1)=1,K(2)=2,K(3)=5は図を書いて、分かるとします。
n=4のときを描きます。
図のような△ABCの最短経路の道筋がK(4)になります。
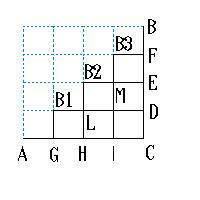
K(4)を求めるのに、
よって、K(4)= K(3)+K(1)K(2)+K(2)K(1)+ K(3)
=5+1×2+2×1+5=14 になります。
これは、一般に K(0)=1と決めておけば、また、こんな数え方(書き込み方式)もできます。
14B
↑
5→14F
↑ ↑
2→5→9E
↑ ↑ ↑
1→2→3→4D
↑ ↑ ↑ ↑
A→1→1→1→1C
さらに、斜めの線に関しての対称性に気がつけば、
K(4)= 1×1+3×3+2×2=14
K(5)= 1×1+4×4+5×5=42
K(6)= 1×1+5×5+9×9+5×5=132
したがって、カタラン数K(n)は何個かの平方数の和でできています。
さて、本題に入ります。n=4で描きます。
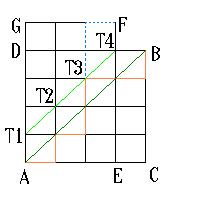
□DACBの最短経路の道筋は、階乗の記号を使えば、
(4+4)!÷(4!×4!)=70 通り あります。
ここから、対角線ABと交わる経路が不適ですから、
この不適な経路を求めます。
例えば、図の太線の経路は不適ですが、
これを直線T1T4について対称移動します。
ただし、直線T1T4に始めて出会った点から
後の部分のみを対称に曲げて図の太い波線を考えると、
全ての不適な経路は□AEFGの最短経路の数に等しくなります。
これは、 (5+3)!÷(5!×3!)=56 通りとなり、
求めるカタラン数K(4)は、
K(4) =8C4−8C3
=70−56=14 になります。
一般に、
K(n) =2nCn −2nCn−1
=2nCn÷(n+1)
となります。
そこで、また、問題です。
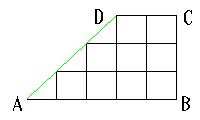
次の台形ABCDの最短経路は何通りありますか。

| NO.660 | '99 11/14 | 水の流れ | 大縄跳び(1) |
太郎さんの勤務している学校で、体育大会で「大縄跳び」競技があり、
こんな問題を考えました。
1直線上に2n人の生徒が並んでいます。 大縄をn本渡して、2人で1組とし、 大縄が交差せずに競技ができるようにします。 このとき、生徒は区別しないで、n本の大縄 の軌跡について、次の問に答えてください。
問題1:
n=1,n=2,n=3,n=4,のときの軌跡の数は何通りですか。
問題2:
一般の場合の軌跡の数を、nで表してください。
太郎さんは、過去に、このような数列を扱ったことを覚えています。

| NO.661 | '99 11/15 | Junko | 大縄跳び(2) |
問題1:
nに対する軌跡の数をF(n)とすると、
n=1 F(1)=1
n=2 F(2)=2
n=3 F(3)=5
n=4 F(4)=14
これらは、図を描いて数えました。
問題2:
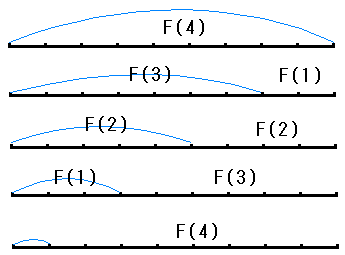
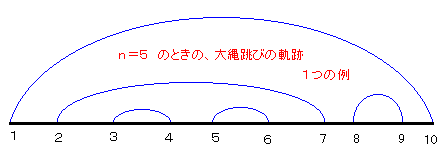
まず n=5の場合について考えてみました。(右図参照)
左から1,2,・・・,10と背番号をつけます。
| F(5) | =F(4)×F(0)+F(3)×F(1)+F(2)×F(2)+F(1)×F(3)+F(0)×F(4) |
| =14×1+5×1+2×2+1×5+1×14 | |
| =42 |
一般的にもこれと同じことが言えるはずですから、
F(n)=F(n-1)×F(0)+F(n-2)×F(1)+F(n-3)×F(2)+・・・+F(0)×F(n-1)

| NO.664 | '99 11/17 | kiyo | 大縄跳び (3) |
この問題は、ベーシック言語のFOR〜NEXT文の構造と同じですね。
水の流れさんの
「カタラン数のレポート」として、
歴史的経過を含めて詳細が報告されています。
Junko先生の一般式の他に色々表現があるようですがシンプル
なのは以下のものではないでしょうか。
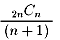

| NO.665 | '99 11/17 | Junko | 大縄跳び (4) |

Combination と言えば、パスカルの三角形です。
2nCn は、左図のように
パスカルの三角形において1段おきに中央に現れます。
これを順に (n+1) で割れば、カタラン数となるわけですね。
{1,2,5,14,42,132,429,1430,・・・}

| NO.666 | '99 11/18 | Junko | 大縄跳び (5) |
縄の左側を持つ人をL、右側を持つ人をRとします。
n個のLとn個のRを1列に並べることを考えます。
ただし縄が交差してはまずいわけですから、左から数えていった時に常にLの数がRの数より等しいか
大きくなくてはなりません。
そう考えると、NO.121 つり銭の問題(1)
と同じだということがわかります。
 更に、NO.127 つり銭の問題(3)で、
「水の流れ」さんがおっしゃっているように、Lを「→」、Rを「↑」で表せば、
まさにこれを1列に並べることと同じです。
更に、NO.127 つり銭の問題(3)で、
「水の流れ」さんがおっしゃっているように、Lを「→」、Rを「↑」で表せば、
まさにこれを1列に並べることと同じです。
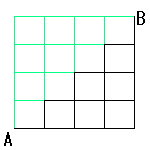
もちろん、左から数えて常に「→」の数が「↑」の数より等しいか
大きくなくてはなりません。
それは左図(n=5)で、AからBへ黒い道だけを通って行く行き方を数えればよいということになります。

| NO.668 | '99 11/20 | 水の流れ | 大縄跳び (6) |

カタラン数はパスカル三角形の中で、
F(n)=2nCn-2nCn-1という観点から、
偶数段の中央値を n+1で割らなくても、中央値をから隣の数字を引くと生まれてきます。

 戻る
戻る