
Weekend Mathematics/コロキウム室/テーマ別/28.三角数は平方数?
| NO.571 | '99 7/12 | 水の流れ | 三角数は平方数?(1) |
太郎さんは、高校でパスカルの三角形の美しさを教えています。
そこで、問題です。
問題1:
x2=2y2+1(一つのペル方程式)である、
正の整数解(x、y)を求めてください。
一部の特殊解でも良いですし、一般解でも良いです。
問題2:
子供とき、おはじきで遊んだことがあります。
正方形に並べたおはじきをくずして、
今度は正三角形にも並べることができたとき、
これらのおはじきの個数を求めたくなりました。
1つの例でも良いですし、一般の場合でも良いです。
皆さん、考えてください。
太郎さんも童心にかえって、いろいろとおはじきを並び替えて、
考えていましたが、なかなかうまくいきません。
皆さんも、考えてください。

| NO.572 | '99 7/12 | kiyo | 三角数は平方数?(2) |
(1)
(X,Y)=(3,2),(17,12),(99,70),(577,408)・・・
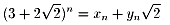
(2)
36,1225,41616,1413721,48024900,・・・
漸化式
C(1)=0,C(2)=1
C(n)=34・C(n−1)−C(n−2)+2
前回と同じアプローチです。

| NO.575 | '99 7/13 | Junko | 三角数は平方数?(3) |
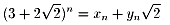 なる(xn,yn)が、
方程式x2=2y2+1 の解であることを
数学的帰納法で示します。
なる(xn,yn)が、
方程式x2=2y2+1 の解であることを
数学的帰納法で示します。
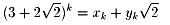 に対して、
xk2=2yk2+1 とする。
に対して、
xk2=2yk2+1 とする。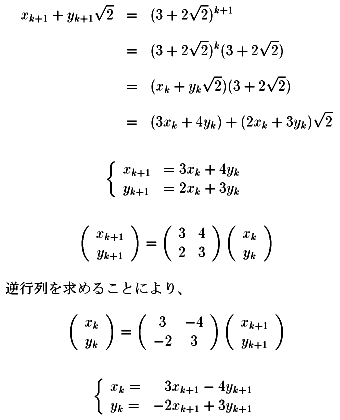
これを、xk2=2yk2+1 に代入する
ことにより、xk+12=2yk+12+1 を
得ますから、
数学的帰納法により証明されます。
しかしながら、これは
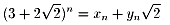 なる(xn,yn)が、
方程式x2=2y2+1 の解であることを
示したにすぎず、方程式x2=2y2+1 を解いたことにはなりません。
なる(xn,yn)が、
方程式x2=2y2+1 の解であることを
示したにすぎず、方程式x2=2y2+1 を解いたことにはなりません。
「方程式を解く」というのは、それを満たす解を”すべて”求めることだからです。

| NO.577 | '99 7/15 | Junko | 三角数は平方数?(4) |
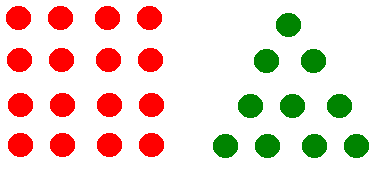
一辺aの正方形のおはじき個数は
一方、一辺bの正三角形のおはじきの個数は、
1+2+3+・・・+b=1/2・b(b+1)
これが等しければいいので、
1/2・b(b+1)=a2
b(b+1)=2a2
左辺を平方完成すると、
(b+1/2)2−1/4=2a2なので、
b+1/2=cとおく。
そうすると、c2−1/4=2a2 となり、
4c2−1=8a2
(2c)2=2(2a)2+1 となる。
さらにここで、2c=x、2a=yとすれば、
X2=2y2+1 となり、ペルの方程式に帰着される。
ここで、a,bは正のの整数なので、x=2b+1,y=2aも正の整数である。
NO.572で「kiyo」さんが、示してくださった解をあてはめてみます。
x=3、y=2のとき、a=1/2・y、b=1/2(x-1)より、a=1、b=1。
このとき、おはじきの個数は1個。
x=17、y=12のとき、a=6、b=8。このとき、おはじきの個数は36。
x=99、y=70のとき、a=35b=49。このとき、おはじきの個数は1225。
・・・

| NO.579 | '99 7/17 | Junko | 三角数は平方数?(5) |
一般の「ペルの方程式: X2=k・y2+1」・・・(*)
について考えてみます。
これを満たす解が1組みつかったとしたら(存在する保証はどこにもないのですが・・・)
これを、
x1=a、y1=bとして、
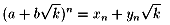 なる(xn , yn)を考えます。
なる(xn , yn)を考えます。
これもやはり方程式(*)の解になることが>NO.575と
同様に数学的帰納法で証明されます。

 戻る
戻る