コロキウム室(ヘロンの三角形)

第２１回数学的な応募問題

太郎さんは、高校で三角形の面積を求めるのに、 ヘロンの公式を教えています。 そこで、３辺の長さとその面積がともに整数となる三角形を ヘロンの三角形と言います。 だから、この性質を持つ三角形を知っていたいと、思っていました。 ここで、特に、３辺の長さが連続する３つの自然数の場合を考えます。

問題１：
ｘ^２＝３ｙ^２＋１（一つのペル方程式） である、負でない整数解（ｘ、ｙ）を求めてください。 一部の特殊解でも良いですし、一般解でも良いです。

問題２：
３辺の長さが連続する３つの自然数で、 その面積も整数である三角形の例をいくつか、 考えてください。

太郎さんも童心にかえって、いろいろと数字を順に変えて、 考えていましたが、　なかなかうまくいきません。 皆さんも、考えてください。　

1. （Ｘ_１＝２，Ｙ_１＝１）， （Ｘ_２＝７，Ｙ_２＝４），・・・
   

   一般には次の式で与えられます。

   
   
   

2. 簡単なベーシックのプログラムを組んでいくつか例を出して数列サイトでカンニングしました。

   　
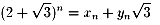
   　　FOR I=1 TO 100000
     　　 FOR J=I+1 TO I+1
         　　FOR K=J+1 TO J+1
          　　  LET  S=(I+J+K)/2
          　　  LET  S1=(S*(S-I)*(S-J)*(S-K))^0.5  ヘロンの公式
          　　  LET  S2=INT(S1)
          　　  LET  S3=S1-S2
          　　  IF S3=0 THEN PRINT I;J;K;S1　条件を満たす３辺と面積
         　　NEXT K
      　　NEXT J
   　　NEXT I
   END
   

   
   
   

   辺 a	辺 b	辺 c	面積
   ３	４	５	６
   １３	１４	１５	８４
   ５１	５２	５３	１１７０
   １９３	１９４	１９５	１６２９６
   ７２３	７２４	７２５	２２６９７４
   ２７０１	２７０２	２７０３	３１６１３４０
   １００８３	１００８４	１００８５	４４０３１７８６
   ３７６３３	３７６３４	３７６３５	６１３２８３６６４

   
   
   　１番短い辺をＨ（ｎ）とする。 漸化式は、
   Ｈ（１）＝３，Ｈ（２）＝１３
   Ｈ（ｎ）＝４×Ｈ（ｎ−１）−Ｈ（ｎ−２）＋２　となっていました。
   Ｈ（３）＝４×１３−３＋２＝５１
   Ｈ（４）＝４×５１−１３＋２＝１９３
   

三角形の三辺の長さをａ，ｂ，ｃとしたときに面積Ｓを与える次の式を、 へロンの公式と呼んでいます。

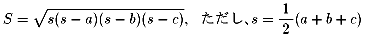
さてここで、三角形の３辺は連続した自然数ということですから、 ｂ−１，ｂ，ｂ＋１とします。

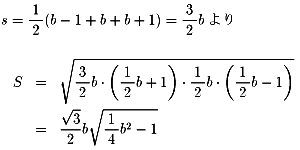
面積Ｓが整数となるためには、ｂは遇数である必要があります。 そこで、ｂ＝２ｋとおきます。（ｋは正の整数）

ｋはもちろん正の整数ですから、これで問題１の方程式ｘ^２＝３ｙ^２＋１に帰着されたわけです。
NO.558で、「kiyo」さんが求めてくださった解を２，３代入してみます。

• ｒ_１＝１，ｋ_１＝２とすると、
  ｂ＝２ｋ＝４、従って３辺の長さは３，４，５、面積は６
  
• ｒ_２＝４，ｋ_２＝７とすると、
  ｂ＝２ｋ＝１４、従って３辺の長さは１３，１４，１５、面積は８４
  
• ｒ_３＝１５，ｋ_３＝２６とすると、
  ｂ＝２ｋ＝５２、従って３辺の長さは５１，５２，５３、面積は１１７０
  

ヘロンの三角形の一般式。
三辺を、Ｂ−１，Ｂ，Ｂ＋１とする。 漸化式は、 Ｂ（ｎ）＝４・Ｂ（ｎ−１）−Ｂ（ｎ）
特性方程式は、Ｘ^２−４Ｘ＋１＝０

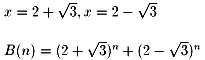
他の２辺はプラス、マイナス１となる。

NO.558
x_１＝２，y_１＝１, 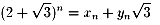から、 （x_ｎ，y_ｎ）の一般項を出してみます。

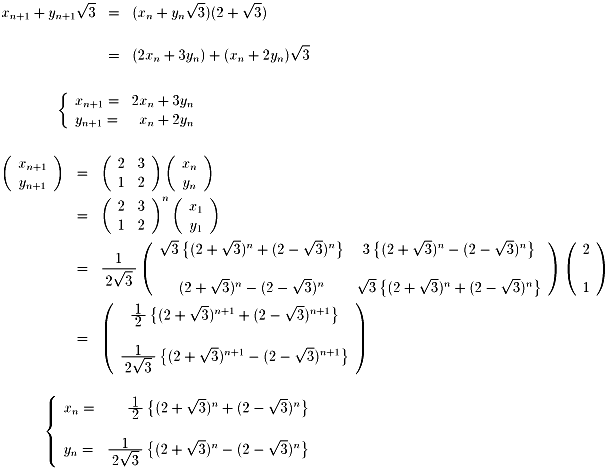
行列のｎ乗の計算についてここでは省略させてください。
計算間違いをしていないといいのですが・・・。

コロキウムNO.558の１について これは３の平方根の有理数による近似です。

少なくとも私はそのように理解しています。