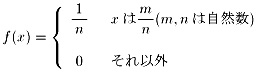
とする。 xが無理数のとき、f(x)が連続であることを証明せよ。
Weekend Mathematics/コロキウム室/テーマ別/24.連続の証明
| NO.511 | '99 6/3 | 月の光 | 連続の証明(1) |
昨日友達にこんな問題を聞かれました。
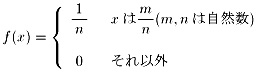
とする。
xが無理数のとき、f(x)が連続であることを証明せよ。
僕はこう考えました。

どうしたらいいでしょうか。
追加
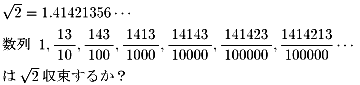

| NO.514 | '99 6/4 | Junko | 連続の証明(2) |
この問題はきっちりいかないといけないかなと思います。
まずは、連続性の定義から
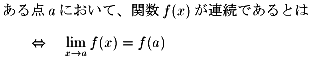
逆に連続でない例をあげましょう。
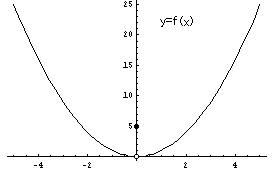
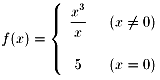
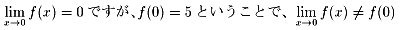
つまり x=0で不連続です。
もう1つ例を上げます。
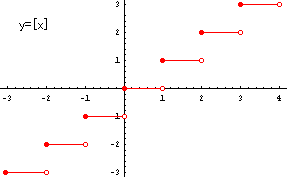
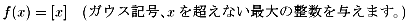
これは、すべての整数値で不連続です。
例えば、x=1において連続でないことを示します。

ですから、f(1)=1と一致するかどうか議論する以前の問題です。
(厳密にいえば、左極限と右極限が一致して初めて極限の存在がいえることになります。)
右極限と関数値は一致していますけれどね・・・それだけではだめなのです。
この続きはまた次回・・・。

| NO.515 | '99 6/4 | Idaho Potato | 連続の証明(3) |
あっさり答を披露してしまうとおもしろくないので、 少々遊んで(失礼!)みます。
月の光さんがNo.511に示した「連続性の証明」は、 次の命題が成り立つことを前提としています。
それなら、No.511の証明を次のように修正すればよいことになります。
a を無理数とする。 Sn = a - 1/10n, Tn = a + 1/10n とすると、 数列 { Sn }, { Tn } は、 それぞれ単調増大、単調減少で、いずれも a に収束する。 しかも、すべての n について、 Sn, Tn は無理数なので、 f(Sn) = f(Tn) = 0 = f(a) である。 したがって、命題Aにより、関数 f は x = a で連続となる。それところが、もし命題Aが正しいならば、 上の証明と全く同じ考え方で、次の命題を証明することができます。
何かおかしいと思いませんか?
ちょっと考えればすぐわかることですが、実は、
命題Bの関数 f は、
「いたる所『不連続』な関数」の典型的な例なのです(ディリクレ関数といいます)。
そういうわけで、 月の光さんの証明が正しくないことの本当の理由は、 もっと根本的なところにあるのです。 「m/n は既約分数」云々というのは、細かい技術的な問題であって、 本質的ではありません。
実は、
No.511の関数の(無理数の点における)連続性を証明するには、
「関数が連続であるとはどういうことか」という、
大学教養課程の解析学の基礎知識が本質的に必要になるのです。

| NO.516 | '99 6/5 | Junko | 連続の証明(4) |
「ε-δ(イプシロン−デルタ)論法」というのを紹介します。
(極限をきちんととらえようとするとき、
避けては通れないのですよね。)

εによって、どんなに小さい区間を与えられたとしても、
それなりに(εにdependした形で)区間(a-δ,a+δ)をとってくれば、
その区間内にあるxに対するf(x)の値を、(α-ε,α+ε)内に納めることができる、
ということです。

| NO.523 | '99 6/7 | プ−太 | 連続の証明(5) |
NO.516 連続の証明(4)でjunkoさんが、
連続や極限の定義を厳密のおこなう為にεーδ論法
をあげていましたが、別な方法もあることを紹介します。
実数列の極限


| NO.524 | '99 6/7 | Junko | 連続の証明(6) |
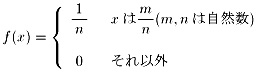
とする。
xが無理数のとき、f(x)が連続であることを証明せよ。
これをεーδ論法で証明してみます。


| NO.528 | '99 6/12 | Idaho Potato | 連続の証明(7) |

| x - a | < δは、 0 < | x - a | < δが正当。
なぜなら、x = a を除外しておかないと、
f(a) = αを含意することになり、結果的に、
「極限の定義」ではなく、「連続性の定義」になってしまいます。
NO.524
証明の3行目以下での δ の選び方:
「そのような δ は必ず存在する」で済ませても
よいかもしれませんが、たとえば、次のようにすれば、
δを具体的に選び出すことができます。
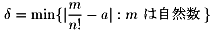
右辺の値が存在して、しかも 0 でないことは、
a が無理数であることからわかります。

| NO.529 | '99 6/12 | Idaho Potato | 連続の証明(8) |
No.524でJunkoさんが 「連続の証明」を完結してくれたところで、 ε-δの意味や背景について、少し考えてみましょう。
「関数が連続である」という言葉から、
どのような状態を想像しますか?
たいていの人は、その関数のグラフを考えて、
「グラフの線がつながっている」というイメージでとらえると思います。
その「イメージ」をもう少し明確にするためにつくられたのが、
「関数の極限」という概念を用いた連続性の定義です。
それでは、「関数の極限」とは何でしょうか?
高校の教科書では、「極限」に対する素朴なイメージを、
「限りなく近づく」などという表現で説明しています。
しかし、このような直観的な説明だけでは、
極限の概念を数学の対象として扱うためには不十分です。
そこで、数学的に厳密で曖昧性のない形で、
「限りなく近づく」ということの意味を明確にするために考え出されたのが、
ε-δを用いた極限の定義なのです。
そして、ε-δによって厳密に定義された極限の概念を用いることによって、 関数の連続性も、数学的に厳密に定義されるのです。
ところで、こうして定義された「関数の連続性」というのは、
私たちが持っている「連続な関数」に対する直観的なイメージを正しく反映しているのでしょうか?
No.511の問題は、
まさにこのようなことを私たちに問いかけていると思います。
「連続 = グラフの線がつながっている」という立場で考えると、
No.511の関数は、そもそもグラフを描くこと自体が困難(不可能?)ですし、
想像力をたくましくしてグラフを思い浮かべてみても、
それは、とても「線がつながっている」などと形容できるものではありません。
ところが、ε-δによって定義された「連続性」の概念というのは、
このような、一見「連続」とは思えないような関数をも含んでしまうのです。
ε-δによる連続性の定義というのは、
「連続性の概念を厳密に定めて、
数学の対象として扱えるようにする」という数学的な要求は、
確かに満たしています。
しかし、
「関数が連続であるとはどういうことか」という「哲学的」な問いに対しては、
必ずしも十分な答えを与えているわけではないように思えます。

| NO.534 | '99 6/16 | 月の光 | 連続の証明(9) |
NO.516連続の証明(4)の証明で、
|x2-4|=|(x+2)(x-2)|<|x+2||x-2|とありますが、
ここは”=”ではないでしょうか?
また、δ<min(ε/8 ,√ε/2)の意味を教えて下さい。

| NO.536 | '99 6/17 | Junko | 連続の証明(10) |
確かに|x2-4|=|(x+2)(x-2)|=|x+2||x-2|ですね。ごめんなさい、勘違い!
δ<min(ε/8 ,√ε/2)としたのは、最後に|x2-4|<εとしたかったために作為的にそうしたのです。
問題はδのとり方ではなくて、δの存在です。
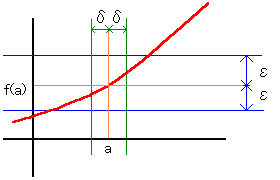
連続なところ(x=a)では、どんなに小さいεを提示されたとしても、
それに応じてδを設定することができます。
そして、
「0<|x-a|<δ ならば、|f(x)-f(a)|<ε」とはできるわけです。
つまり、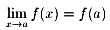 という
わけです。
という
わけです。
不連続な場所ではδが存在しないという例を挙げましょう。

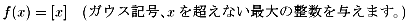
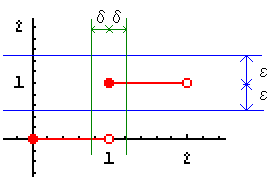
この関数はx=1において不連続です。
εは任意ですから、仮にε=1/2とします。
すうするといかなるδをもってしても、
「0<|x-1|<δ ならば、|f(x)-f(1)|<ε」とはできません。
δをどんなに小さくとったとしても、区間(1-δ,1+δ)の属するxに対するf(x)をすべて
(f(1)-ε,f(1)+ε)=(1/2,3/2)に納めることはできないからです。
具体的には、区間(1-δ,1+δ)の属するx=1-δ/2とすると、
これに対するf(x)=0ですから・・・。
つまり、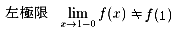 です。
です。

| NO.1096 | 2001.11.18. | fermeil | 連続の証明(11) |
NO.524 連続の証明(6)連続の証明(6)の記事の下から3行目の f(x)<1/n
はなぜいえるのでしょうか?

| NO.1099 | 2001.11.19. | Junko | 連続の証明(12) |
「f(x)<1/n はなぜいえるのでしょうか?」
逆に言うと、f(x)>=1/nになるようなxをすべて排除したからです。
無理数aの前後には、無限に有理数存在します。
つまりf(x)=0とならないxが無限に存在します。
しかしながら与えられたεに対して、f(x)<1/n<εとすることはできます。
それは適当なδ、(a-δ,a+δ)の中からf(x)>=1/nとなるxをすべて排除すればいいのです。
それは高々有限個ですから、δを小さくとることで可能なのです。

 戻る
戻る