Weekend Mathematics/コロキウム室/テーマ別/23.ダーツの確率
NO.462 '99 5/5 水の流れ ダーツの確率
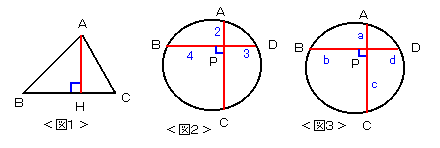
太郎さんのお子さんは中学生です。次のような問題をもらって来ました。

太郎さんは、先日のゴールデンウイークにある電気店の大売り出しに
行って来ました。ここで、問題です。
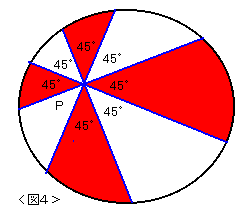
太郎さんは童心にかえって、ダーツ競技を楽しんでいましたが、
当たりとはずれの確率が気になってしかたがありません。
皆さんも、考えてください。

NO.465 '99 5/8 Junko ダ−ツの確率(2)
NO.462の 「ダ−ツの確率」についてとりあえず3番まで。



| NO.487 | '99 5/22 | Junko | ダ−ツの確率(3) |

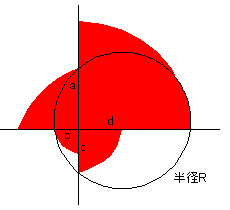
円の4分割は任意ですから、これもまたおもしろい結果だなあと思うのです。

| NO.498 | '99 5/26 | Junko | ダーツの確率(4) |
この問題についてず−っと考えていました。
確率は1/2だそうなあ、と見当をつけていましたが、
はっきりとした根拠を示せずにいました。
また、NO.465で1〜3までの
ヒントに対する解答は得られたのですが、それがどうして4につながっていくのか
わかりませんでした。
幸いにして、このコロキウム室で極座標系による積分を話題にしていくうちに、
だんだんと道が開けてきました。
今日またこの問題を考えていて、「わかった!」と叫んでしまいました。
もやもやしていた霧が一気に晴れたような感じです。
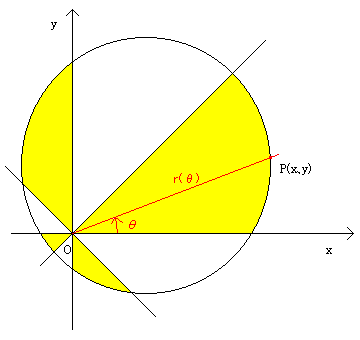
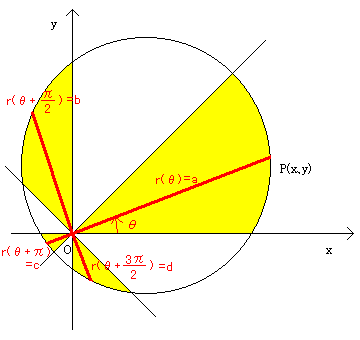
4本の弦が1点で交わっているところを原点に、左上の図のようにダ−ツの的をおきます。
円周上の点P(x,y)と原点を結ぶ線分OPとx軸とのなす角をθとします。
0P=r(θ)とし、極座標系による積分を考えます。
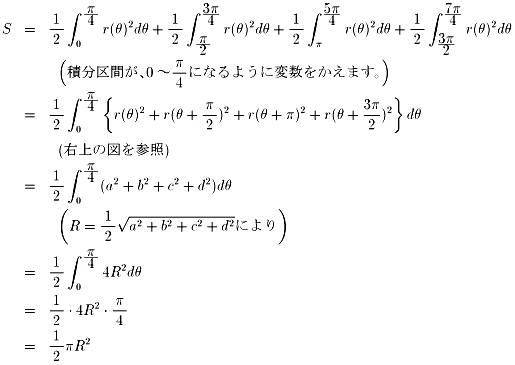

 戻る
戻る