コロキウム室(素数の逆数の総和)

NO.359　　　　'99 2/23 　　 月の光 　　　 素数の逆数の総和
　　

調和級数が発散する事は示されましたが、 素数の逆数の総和はどうでしょうか？
素数が無限に存在する事をまず示してから考えてみて下さい。

NO.383　　　　'99 3/5 　　 水の流れ 　　　 素数の逆数の総和 （２）
　　

問題１「素数は無限に存在するか」
＜証明＞コロキウム室のNO.373 で証明されたように調和級数が＋無限大に発散します。
もし、素数が有限個しかなければ、右辺のΠ１／（１−１／ｐ）は有限の値になり、 ＋無限大に発散することに反します。よって、素数は無限に存在します。

問題２「素数の逆数の総和は＋無限大に発散する」
＜証明＞コロキウム室のNO.377 で証明された（１）を使います。

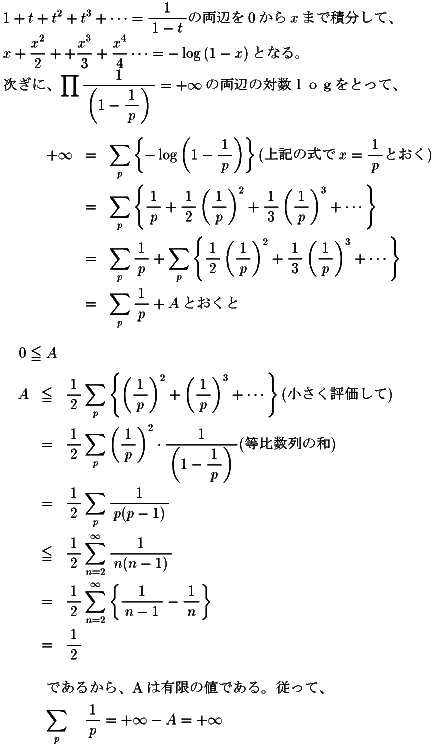
すなわち、素数の逆数の和は＋無限大に発散する。
＜この証明は過去の「大学への数学」に載っていました＞

NO.404　　　　'99 3/14 　　 Junko 　　　 素数の逆数の総和（３）
　　

素数が無限に存在することの、オ−ソドックスな証明です。
背理法によります。

もし素数の数が有限個だとして、それを小さい順に ｐ_１、ｐ_２、ｐ_３、・・・、ｐ_ｍとします。
新たに、(ｐ_１・ｐ_２・ｐ_３・・・ｐ_ｍ＋１)なる数を考えます。
この数は、任意の素数ｐ_ｎで割れませんので、素数です。 しかも、最大の素数であるｐ_ｍよりも大きい数であり、 これは明らかに矛盾です。

NO.405　　　　'99 3/14 　　 Junko 　　　 素数の逆数の総和（４）
　　

大学時代のゼミで読んだ「An Introduction to the Theory of Numbers」の中に、 素数の逆数の和が発散する事の証明がありますので、紹介します。

素数を小さい方から順に、 ｐ_１、ｐ_２、ｐ_３、とします。

このことから逆に素数が無限に存在することが言えると思います。 もし素数が有限個しかなかったら、上の級数が発散するはずはないからです。