コロキウム室(宇宙空間での最短経路問題)

NO.353　　　　'99 2/22 　　 Junko 　　　 宇宙空間での最短経路問題（２）
　　

NO.313で、 立方体の８つの頂点を最短で結ぶにはどうしたらよいかという問題が 提示されています。

実験してみました。
ストロ−の中に糸を通して立方体(正六面体)を作り、 それをシャボン液にひたします。 そして静かに引き上げると、写真のような状態になります。 中央に、シャボン液による立方体ができています。 不思議ですよね？

ついでなので、正四面体も作ってみました。
写真だとわかりづらいのですが、 中心に向かって二等辺三角形の膜が６枚張られます。 結構きれいにできるので、感動します。

正八面体もやってみました。中に菱形のような膜ができて、 これもまたきれいです。
なかなかうまく写真に撮れないので、これは是非実験してみてください。
用意するものは、ストロ−と糸とシャボン液。 すぐにできますから、是非やってみてください。 楽しいです。

NO.372　　　　'99 3/1 　　 Weadore 　　　 宇宙空間での最短経路問題（３）
　　

NO.353で求められた ネットワークが最小でないことを示す。
まず、最小のネットワークはある任意の点からたの全ての点に 行ければ良いので、閉じた回路をもっていない。 これは、かりにA→Bに行くとしよう。その時に、A→B に直接行く方法が二つ以上はないのです。 なぜなら、一つあれば十分なので、他をなくしても 問題ないからです。
また、ここで[No.353]のネットワークは閉じた回路を 明らかに含んでいます。よって、ネットワークは 最短ではない。
例を挙げてみますと、あの中央の立方体の 手前の四辺を取ってみましょう。 このとき、任意の点が他のすべての点へ 行けることを確かめましょう。 ね？行けるでしょう？遠回りだけれど。
また、その取ったネットワークは明らかに ネットワークの重みが釣り合ってない。 よって、そのネットワークも最短ではない。
多分あの実験では、二次元のネットワークしかできないでしょう。 事実、あの実験でやったのは、二次元のシュタイナーのネットワーク を釣り合わせただけですしね。
でも、ちなみに、正四面体はあのネットワークが最小です。 それは、これから証明します。お楽しみに。

NO.382　　　　'99 3/4 　　 Weadore 　　　 宇宙空間での最短経路問題（４）
　　

NO.353 の正四面体のネットワークが最短であることを示す。

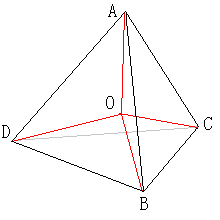
まず、正四面体ABCDの内部にある点Oをつないでできる。 AO+BO+CO+DOの最短のネットワークについて議論をする。
AB，CDと平行でO点を通る平面と、ABの中点とCDの中点 を結んでできる線分との交点をO'とする。
ここで、点Aの上記で定義した平面と対象な点をA'とすると、 A'とBを結んだ線分とその平面との交点がO'になる。
よって、AO + BO = A'O + BO≧A'O' + BO' =AO' + BO'
∴AO + BO ≧ AO' + BO'
同様に、CO + DO ≧ CO' + DO'
よって、OはABとCDとの中点同士を結んだ線分上 に存在する。また同様に、ADとBCの中点同士を結んだ 線分上にも存在することになる。
よって、この条件を満たす点Oは正四面体ABCDを内接する 球の中心となります。
また、正四面体の内部に２点、点が存在したときは、 ネットワークの重みが明らかに釣り合わない。 また、三点以上存在しても、今度は閉じた回路を持ってしまう。
よって、[No.353]でできたネットワークが最短であることが示された。
次回は、本題である正六面体について議論をします。お楽しみに。

NO.388　　　　'99 3/8 　　 Weadore 　　　 宇宙空間での最短経路問題（５）
　　

NO.313の答の予想です。

前回の正四面体のネットワークより、次のような 正多面体の予想を立てました。

☆予想
正多面体の最短のネットワークは、 正多面体の一面を真正面から見たときに見える輪郭の 平面図形、又はその一面自身の図形の平面図形の 最短のネットワークが成り立っているものがあり、 また、その成り立っている面の数は正ｎ面体の場合、 ｎ以下のｎに一番近い又は同じである２のべき乗個ある。

ちなみになぜ２のべき乗を考えたかというと、 正多面体の公式、ｐを面数、ｑを角数、ｒを辺数とすると、 ｐ＋ｑ−ｒ＝２が成り立つことから来ています。
これは正四面体では成り立っています。
ここで、その予想を正六面体に当てはめる。
つまり、一面を真正面に見たときにできた図形、 正方形の最短のネットワークが４個できるはずである。
ここで、正方形の最短のネットワークはシュタイナーのネットワークであり、 また、立方体の四面から見てこのシュタイナーのネットワーク ができるのは４つが最大である事もわかる。
よって、僕の考えた予想が正しければ、正六面体の 最短のネットワークは上の条件を満たしているはずである。
このネットワークを作り、その値も計算しておくと、 一辺の長さが１の正六面体であれば、
(17-√3)/3となります。（複雑なので途中計算略）

予想の反例は歓迎です。 あと、計算もあまり自信はありません。 数学なのに字ばっかりですいませんでした。m(__)m

NO.393　　　　'99 3/10 　　 水の流れ 　　　 宇宙空間での最短経路問題（６）
　　

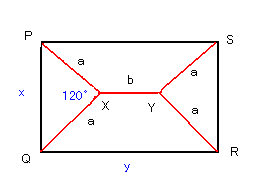
＜１＞　本題に入る前に平面上で、長方形ＰＱＲＳを考えます。
短い辺の長さをＰＱ＝ｘ、長い辺の長さをＱＲ＝ｙとします。
ここで、図をみてください。
　　　　∠ＰＸＱ＝∠ＰＸＹ＝∠ＱＸＹ＝１２０゜
　　　　∠ＲＹＳ＝∠ＲＹＸ＝∠ＳＹＸ＝１２０゜
となる点Ｘ、Ｙをみつけます。これがシュタイナー点です。
このとき、ＰＸ＝ａ，ＸＹ＝ｂ　として、ａ，ｂをｘ、ｙで表すと、
ａ＝（ｘ／２）÷ｃｏｓ３０゜＝ｘ／√３，
ｂ＝ｙ−ｘ／√３
よって、４点Ｐ、Ｑ、Ｓ、Ｔを結ぶ最短ネットワークは
４ａ＋ｂ＝ｙ＋√３ｘ
　この場合　ｘ＝１，ｙ＝１　より　　
　 ２（４ａ＋ｂ）＋１＝３＋２√３≒６．４６４　となります。
勿論、これが求める最短経路ではありません。 この続きは明日にします。

NO.395　　　　'99 3/11 　　 水の流れ 　　　 宇宙空間での最短経路問題（７）
　　

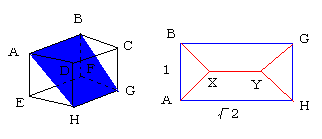
空間における最短経路＜２＞を送ります。
昨日、上面・底面ともシュタイナーのネットワークで結ばれて、 上面から底面までの高さ１を加えて、
（３＋２√３）≒６．４６４　を求めました。
ところで、図のように長方形ＡＢＧＨとＣＤＥＦにおいて、 ４点のシュタイナーのネットワークを考えてみると、

前回の２（４ａ＋ｂ）＝ｙ＋√３ｘに、ｘ＝１，ｙ＝√２を代入して
　　　　　　　　　　＝２（√２＋√３）

　　　　　　　　　　≒６．２９２　　　となります。

NO.399　　　　'99 3/13 　　 水の流れ 　　　 宇宙空間での最短経路問題（８）
　　

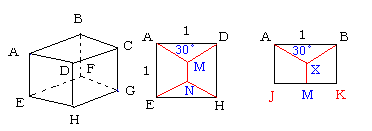
＜３＞前回は２つの平面ＡＨＧＢとＣＤＥＦは４５度で交わっています。 だから、この２つの平面の４点を結ぶシュタイナー点は立方体のど真ん中で 交わる２直線のなす角が９０度になります。
あくまでも３点を結ぶ最短ネットワークはなす角が１２０度になっていなけれ ばなりません。
だから、NO.393 ＜１＞での上面ＡＤＣＢと底面ＥＨＧＦのネットワークにお いて、上下の中央線の中点Ｍ、Ｎをすべて１２０度の角度を保ったまま立方体の 中心に引っ張っていきます。
これを横の面ＡＥＨＤでみます。 平面ＡＢＸＭは真横からみると、線ＡＭ上に重なっています。 そこで、横の面ＡＥＨＤを結ぶ最短ネットワークも当然、 点Ｍ、Ｎは下がりながらシュタイナー点になります。 すると、図を見てください。 ∠ＤＡＭ＝３０°になります。 後は計算すれば求める結果になります。
ここからはコロキウム室の愛好者の皆さんに求めてもらいます。 お願いします。
なお、この最短ネットワークを発見したのはロウフボロフ大学の ジョン・カストロ氏です。

それでは問題です。
「１辺１の正５角形の最短ネットワークの設計図とその長 さを求めてください。」
＜参考文献：ＢＬＵＥ　ＢＡＣＫＳの数学パズル・パンドラの箱；講談社＞