オイラーが解を得ています。
Weekend Mathematics／コロキウム室／テーマ別
／14.定義域
NO.272 '99 1/11 月の光 定義域（１）
オイラーが解を得ています。
NO.275 '99 1/12 Junko 定義域（２） 定義域というのは文字通り「定義」するものですから、自由に設定できるはずです。
従ってこの問題は最大限定義できる範囲と解釈することにします。
逆関数を考えて、その値域(Ｙのとりうる範囲)を求めればいいのでしょうか？
こちらの定義域は、ｘ＞０と考えられますから、
この時の値域を考えることにします。
NO.279 '99 1/13 Junko 定義域（３）
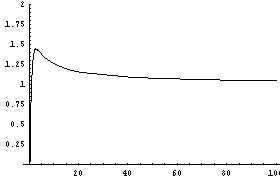
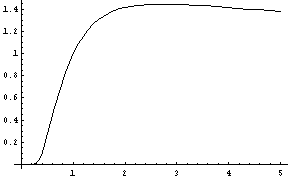
NO.282 '99 1/14 ３−６ 定義域（４）
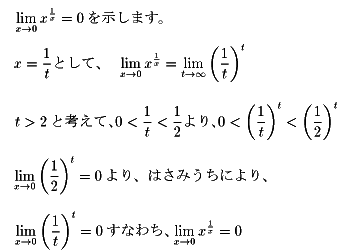
NO.283 '99 1/14 Ｉ．Ｔ． 定義域（５）
NO.284 '99 1/14 水の流れ 定義域（６）
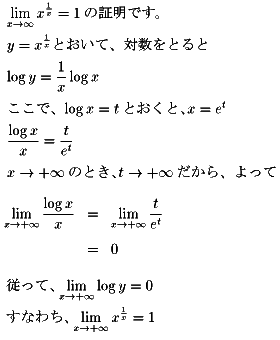
NO.397 '99 3/12 豊作 定義域（７）
NO.272 定義域（１）で出された問題は、結局「同
（２）、
（３）」
で解決
したのだろうか？
確かめたくても肝心の
問題文が意味不明なので
確かめようがない。
NO.402 '99 3/14 月の光 定義域（８）
NO.272を書き直します。
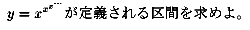
つまり、あるｘに対してｙの値が存在し、一つに定まる区間と考えて下さい。
例えば、ｘ＝０だったらｙは０と１二つの値になるので０は入らない。
ｘ＝−２は途中で虚数になるのでこれも入らない。
ｘ＝√２だとｙ＝２になるので問題の区間内にある。ということです。
NO.406 '99 3/14 豊作 定義域（９）
NO.272の問題はつまり
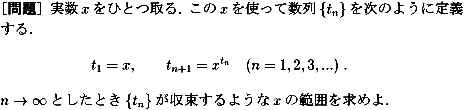
という問題であるという解釈でよろしいでしょうか？
NO.419 '99 3/24 豊作 定義域(10)
NO.457 '99 5/3 月の光 定義域(11)
NO.272において次のような問題を出しました。
「関数の定義域を求めよ」という問題はよく目にしたので
普通だと思っていましたが、
junko先生や豊作さんの反応を見るとそうではないようでした。
このことについて次の文章を見つけました。
「オイラーの贈物」Ｐ.５１
オイラーは関数の定義域を”関数が数学的に意味を持つように、 暗黙のうちに定められるもの”とした。このように、関数の定義とはまさに、定義を要するもので 「つぎの関数の定義域を求めよ」というような問題は、 定義域に対するオイラー流の解釈のもとではじめて成り立ち、 現代流に解釈すれば”定義を求める”という極めて奇妙な問いになってしまう。
略
| NO.1353 | 2003.2.4. | MagicianKuma | 定義域(12) |
NO.272から始まる定義域の問題で答えが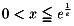 
で結論が出ているよ
うなのですが、
x=-1 は 定義域に入らないのでしょうか？ -1(-1) = -1 , -1^{-1(-1)} = -1 ... で
y=-1 と一意に決まりますが？
戻る