定理:曲線y=f(x)をx軸のまわりに回転してできる立体の側面積は、下の式で表される。
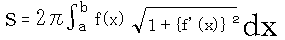
Weekend Mathematics/コロキウム室/2000.7~9/NO.99
| NO.847 | 2000.9.5. | Junko | 回転体の表面積 |
水の流れさんが、HPの「美しい数学の話」第27話の中で回転体の表面積に関する話題を
提供されています。それによると、
定理:曲線y=f(x)をx軸のまわりに回転してできる立体の側面積は、下の式で表される。
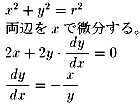
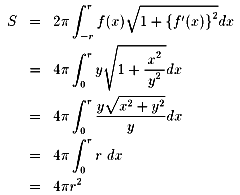

| NO.848 | 2000.9.5. | 月の光 | 複素数の問題(1) |
pを素数、aとbは互いに素な自然数とするとき(a+bi)pは実数にならないこと
を何通りかの方法で証明して下さい。

| NO.849 | 2000.9.6. | Kernighan | 複素数の問題(2) |
c≡(a+bi)p (mod a)とおく。
(a+bi)pが実数と仮定すると c は実数
一方
| c | ≡(a+bi)p (mod a) |
| ≡(bi)p (mod a) | |
| ≡(±bp)i (mod a) (∵pは奇素数) | |
| ≠0 (∵(a,b)=1) |

| NO.850 | 2000.9.10. | 水の流れ | 三角数の数列(1) |
三角数の数列:1,3,6,10,15,21,28,36,45,55,66,78,91,・・・
を自然数nで割ったときの余りを考える。
この余りの中に、n個の整数 0,1,2,3,・・・、(nー1)
のすべてが現れるのは、nがどのような値のときか。すべてのnを求めてください。

| NO.851 | 2000.9.11. | kiyo | 三角数の数列(2) |
プログラムを組んで、周期の位数と問題を推理してみました。
n=2m m:自然数
REM 三角数の法Nの剰余の周期と性質
OPTION BASE 0
LET Z1=11
LET Z=2^Z1 ! 周期の位数の上限
DIM A(Z*2)
DIM B(Z)
REM 三角数の数列の生成
FOR I=1 TO Z*2
LET A(I)=(I*(I+1))/2
NEXT I
FOR I=2 TO Z
FOR K=0 TO Z
LET B(K)=0
NEXT K
FOR J=1 TO Z
LET X=REMAINDER(A(J),I)
LET B(X)=1
NEXT J
LET F=0
FOR K=0 TO I-1
IF B(K)=0 THEN
LET F=1
EXIT FOR
END IF
NEXT K
REM 条件を満たしているかの判定
IF F=0 THEN
PRINT I;
END IF
NEXT I
END

| NO.852 | 2000.9.11. | 水の流れ | 机の積み方(1) |
太郎さんの学校では、年に3回教室の床にワックスをかけて綺麗に磨きます。
そこで、机を廊下に移動して並べることになります。
廊下の左端から順に1列に、机を2段に積み上げます。
作業の効率を考えて、いつも太郎さんは、
左端から詰めながら、下段に机を置いてから上段に置きます。
ここで、生徒の椅子はないと考え、机は同じ物としてください。
(実際のワックスがけのときは、机と椅子を一緒に重ねて置きます。)
また、机の数は2n個があり、奇数個ではありません。
ここで、問題です。
問題1:
この机の積み方は一体何通りあるでしょう。
机が2個、4個、6個、・・・と考えて,下の参考図をみて実際に積んでみてください。
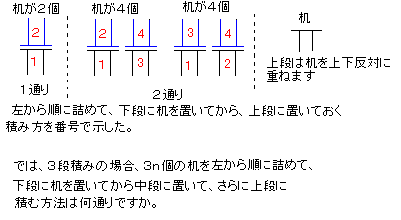
問題2:
もし3段積みにして、左端から詰めながら、下段に机を置いてから中段に、そして上段に置きます。
机は3n個として、このような積み方は一体何通りあるでしょう。

| NO.853 | 2000.9.13. | 水の流れ | ゴールドバッハ予想(1) |
理系への数学10月本を読んでいたら、
イギリスとアメリカの出版社が ゴールドバッハの予想が解けたら1億円(正確には100万ドル)の懸賞金を 2000年3月にかけたと書いてありました。
ケンブリッジ大学教授でフィールズ賞受賞者のアラン・ベーカーさんが 「ゴールドバッハの予想は証明されるかもしれない」と語ったと ニューヨーク・タイムスの記事にあります。とね。
皆さんは、ゴールドバッハの予想は何であったかご存じの方も多いでしょう。
「4以上の任意の偶数は2個の素数の和となっている」という予想です。
さらに、当然かもしれませんが、ゴールドバッハの予想はリーマン予想とも 関連があります。
例えば、1997年に、「一般のリーマン予想」(代数体についてのリーマン予想にあたる) を仮定すると、7以上の任意の奇数が3個の素数の和として表されることが証明されて いるようです。ゴールドバッハの予想が正しければ当然これも正しくなるので、 是非ともはっきりさせたい大切な予想でした。
反例探しにもつながるコンピュ-タによる計算も進められており、 400兆以下の偶数については確認済みだといいます。

| NO.854 | 2000.9.14. | 水の流れ | ゴールドバッハ予想(2) |
昨日「イギリスとアメリカの出版社がゴールドバッハの予想が解けたら1億円
(正確には100万ドル)の懸賞金を2000年3月にかけた」と載せましたが、
理系への数学10月号をよく読んでみると、対象者がアメリカかイギリスの国籍を有する人
と書いてあることを書き忘れました。
さらに、期限(2年?)つきだそうです。追加しておきます。

| NO.855 | 2000.9.14. | もんさん | 2つのツボ |
昔私が読んだ本で面白い問題があったのを思い出したので紹介します。
2つのツボがあります
黒い石と白い石がそれぞれ100個ずつ、混ざって入っています
(ツボには100個ずつと言うわけではありません)
私はツボの中身の石をを自由に移動させる事ができ、
移動した後で目隠しをされ、ツボをシャッフルされます。
(この時ツボの中にかならず石が入っているように移動します)
その後好きな方のツボを選びツボの中の石を1つ取ります。
私は白を選びたいのですが、あなたならどのように
ツボの中の石を移動しますか?

| NO.856 | 2000.9.19. | 水の流れ | ゴールドバッハ予想(3) |
1999年2月号の数学セミナーにゴールドバッハの予想の原稿がありましたので、
ここから引用します。(一部前の原稿と整合性を持たせてあります)
ゴールドバッハ(1690~1764)の予想について、歴史的な事を書きます。 1742年6月7日付けのオイラーへの手紙の中で、ゴールドバッハが述べた観察が、 後に『ゴールドバッハ予想』と呼ばれるようになった問題であり、 それは20世紀末に近い今日もなお、完全に解決されていない難問の1つである。
・・・任意の整数は2つの素数の和として表され、いくらでも多くの素数の和として表されるから、 2より大きい整数は3つの素数の和として表される・・・
ただ、この時代は1も素数の1つとして考えていたのです。
6=3+3、6=5+1,6=1+1+1+1+1+1、6=2+2+2、 6=3+2+1のように表していた。
9=7+2、9=3+3+3、9=5+2+2のようです。
これに対して、オイラーは、同年6月30日付けの返書の中で、 「4以上の任意の偶数は2個の素数の和となっている」が正しいなら、 7以上の任意の奇数が3個の素数の和として表されることを証明が書きてありました。
それによると、「2n+1=2(nー1)+3から明らかであろう」とね。 今では、素数として1を認めないので、ゴールドバッハの予想を次のように述べ直しています。
① 6以上の任意の偶数は、2個の奇素数の和として表される。
② 9以上の任意の奇数は、3個の奇素数の和として表される。
そこで、①ならば②であるから、①を証明すれば良いのですが、歴史の流れはその逆で、 ②の研究とその成功、そして①への応用と未完成というのが現状です。
ゴールドバッハと同じように観察した人達は他にもいます。 デカルトも「整数は1個か2個、または3個の素数の和である」ことに気づいているし、 「ウェアリング」も、彼の著書(1770年)の中に①と②について述べている。 リュカも1891年の著書の中にも書いてあります。
オイラー以降、多くの数学者がゴールドバッハ予想に興味を引かれ考察を重ねて行ったが、 そのほとんどが数値的な実験、すなわち、かなり大きな数についてまで予想が正しいこと を検証するにしか達していなかった。
たとえば、カントールなどの素数表を作り、 1000以下の偶数について①を検証(1894~1895)しています。 続きは、次ぎにします。

 E-mail
E-mail
 戻る
戻る