コロキウム室

確率分布については次の解釈もできます。

１）Ｘがー１になる確率は２／３です

２）３枚目のカードが始めの２枚のカードの間にあるとき、
その値の条件付き期待値は、対称性から（ｎ＋１）／２です。

３）Ｘの期待値は
（−１）×（２／３）＋{（ｎ＋１）／２}×（１／３） より、（ｎ−３）／６になります。

ある高校生から以下のような問題を出題されました。

1. ９だけを９回つかって、１をつくるにはどうしたらいいでしょう。 （ルートはなしで、出切るだけ簡単に。）
   
   
2. 地球を北極南極の立て向きに回る星があります。これは、１時間で 地球を一周します。東京の上空を通ってから 何時間後に再び東京の上空を通るでしょう？
   
   

ｎを自然数とするとき、（ｎ＋１）から２ｎまでの連続するｎ個の整数の積を １から始まるｎ個の奇数の積で割った値を求めてください、ということでした。
式でかくと次のようになります。

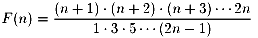
試しにいくつか代入してみます。

n=1 のとき、Ｆ(１)＝２/１＝２

n=2 のとき、Ｆ(２)＝(３･４)/(１･３)＝４

n=3 のとき、Ｆ(３)＝(４･５･６)/(１･２･３)＝８

どうも、Ｆ(ｎ)＝２^ｎではないかという予想がたちます。

分数の分子と分母の個数が同じ、分母は奇数だけ・・・と眺めていて次のことを考えました。
ここに偶数を補ったらどうなるか？
分子については、（ｎ＋１）から始まるというのも不自然なので、１から始めたらどうなるか？

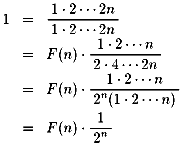
従って、Ｆ(ｎ)＝２^ｎ

1. ９だけを９回つかって、１をつくると言う問題ですが、私が考えた解答を１つ。
   
   ９÷９＋（９−９）×（９＋９＋９＋９＋９）＝１
   
   
2. その星(人工衛星？)は、１時間で１周するとして、地球は自転するから １周してきたときにそこは東京ではないですよね。
   東京が再び同じ場所に戻ってくるのは２４時間後ですから答えは２４時間後。
   実は、時間後に地球が半周したところで、東京の位置はその星の軌道と重なります。 しかし、ちょうど真上というわけにはいかないと思います。
   従って答えは２４時間後と考えたわけです。

「４面体、および６面体に内接する球の体積、外接する球の体積を求めたい」
という問題に関して解答または、参考書、文献等ご存知の方はいませんでしょうか？
指定するのは、各？面体の頂点の座標のみ（４面体ならば、４つの頂点の座標。 ６面体ならば８つの頂点の座標）です。

さて、算太さんからの問題について、１つの方法をお知らせします。

1. ４面体の外接球について：
   これは求める球の方程式を　ｘ^２＋ｙ^２＋ｚ^２＋Ａｘ＋Ｂｙ＋Ｃｚ＋Ｄ＝０　とおいて、
   ４つの頂点の座標を代入して、Ａ，Ｂ，Ｃ，Ｄを決定してください。
   
   
2. ４面体の内接球について：
   まず、３点の通る平面方程式を　ａｘ＋ｂｙ＋ｃｚ＋ｄ＝０　とおいて ３点の座標を代入します。
   ａ：ｂ：ｃ：ｄの比を求めます。 このように４つの平面方程式を求めます。
   次ぎに、求める内接球の中心をＰ（ｐ，ｑ，ｒ）とおいて、 後は、この４つの平面に至る距離が等しいとおきます。
   これは、例の点と平面との距離の公式に代入します。
   ただ、絶対値が入っていますから、　｜□｜＝｜△｜＝｜○｜＝｜◎｜　とね。
   ここで、中心Ｐはそれぞれ４つの平面の正領域か負領域かを見定めてください。
   そして、絶対値をはずして　３元ｐ、ｑ、ｒの連立方程式の計算を行います。
   
   
3. ６面体の外接球について：
   これは、一般的には必ずしも存在するとは限りません。 平行６面体なら可能ですね。
   
   
4. ６面体の内接球について：
   これも、一般的には必ずしも存在するとは限りません。

平成１２年の夏の大会を同じく調べました。ご覧下さい。
夏の全国高校野球は和歌山県の智弁和歌山高校が、 春決勝戦に東海大相模高校に敗れた無念さを胸に、 ３年ぶり２回目の優勝しました。 おめでとうございます。
さて、高校野球は先取点の入ったテームが勝つとよく言われます。 今回を例にして、分析しました。
また、ファンにとって、逆転につぐ逆転の試合は忘れられない感動を与えます。

1. （１）先取点が入って、同点にされてもそのまま終わった試合を�@
2. （２）先取点が入って、逆転して（同点になっても）終わった試合を�A
3. （３）先取点が入って、逆転されても再逆転して終わった試合を�B
   

また、この丸数字の決まったイニングは１回から３回で２５試合 このうち�@のチームが２１チームあります。 ４回から６回で１１試合、７回から９回で１０試合、延長戦の場合が２試合でした。

また、この夏の大会は、先攻をとって勝った試合が２８試合、 後攻が勝った試合が２０試合ありました。必ずしも後攻が有利とはいかなかったようです。

さらに、この暑い中で待たされていることもあって、 １回の表で得点のあったのが１６試合・裏で得点があったのが１０試合もありました。
前半、１回から３回まで両チームが得点のなかったのが、たった１０試合しかありませんでした。

さて、ここで、前回と同じく、野球の試合を行ったとき 「９回裏までのあいだに逆転または勝ち越しが何回起こるか」と言う頻度が、 ”まれにしか起こらないこと”の１例です。 先制点を挙げたチームがそのまま逃げ切ってしまえば、１回も逆転、 勝ち越しがなかったことになる。
そこで、例として、決勝戦の智弁和歌山高校と東海大浦安との得点経過でみます。

２回の表の２点は先制点だから、勝ち越しとは言わない。
３回の裏の２点は逆転だからカウント１します。
４回の表の１点は同点ですので、カウントはしません。
５回の裏の２点は勝ち越しだからカウント２します。
６回の表の２点はこれも同点ですので、カウントはしません
６回の裏の１点は勝ち越しだからカウント３します
８回の表の５点は再逆転ですので、カウント４します
以上、逆転または勝ち越しが回数として４回をカウントします。
この試合が動きの激しい試合であったことを意味しています。

同じようにカウント４の試合は、愛媛県丹原高校と青森県光星学園との試合も８対１０で、 逆転・再逆転・再々逆転・再々々逆転の好試合でした。

逆転・勝ち越しが起った回数

回数	２０００年春のセンバツ	２０００年夏の大会
０　　回	１６試合	２７試合
１　　回	７試合	１５試合
２　　回	５試合	３試合
３　　回	２試合	１試合
４　　回	１試合	２試合

上の表がポアソン分布をしているかをみてみます。
ちょっと、数学の専門的な式になりますが、ポアソン分布の確率密度関数は

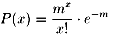　　です。

ここで、ｘは逆転または勝ち越しの回数を代入、ｍはデータの平均値で、この場合は

ｍ＝（１×１５＋２×３＋３×１＋４×２）／４８＝３２／４８＝０．６６６６…

これは、2000年夏の大会は、逆転または勝ち越しが１試合平均０．６６６６回 起こったことを意味しています。
以外と少ないと感じました。皆さんは、どのように思われますか？

逆転・勝ち越しが起こる確率	理論値	実際の試合数
０回　０．５１３４×４８	２４．６４３	２７
１回　０．３４２３×４８	１６．４３０	１５
２回　０．１１４１×４８	５．４７７	３
３回　０．０２５４×４８	１．２１９	１
４回　０．００４２×３１	０．２０２	２

以上、これで、全国大会春・夏４回目の統計でした。

E-mail 戻る