これを有理数表示しますと、1.8=9/5となります。
x>0に対して、指数が有理数の場合m>0ととり、 次のように定義します。
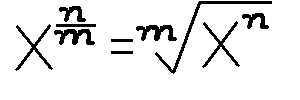
従って、xの1.8乗、つまり9/5乗は、 xを9乗して、5乗根をとればいいわけです。
ところが、ル-ト計算(2乗根)しかできない電卓では、 5乗根は計算できません。
できるのはmが2の何乗かの形にかける時のみということになります。
Weekend Mathematics/コロキウム室/1997/NO.6
NO.39 10/1 Junko
この春からゴルフを始めました。
今日は、箱根湯ノ花ゴルフ場に行ってきました。
コ-スに出るのはこれで3回目です。
スコア? はきかないでください。
でも、おもしろいなあと感じ始めています。
もっと練習して上手になりたいな。
今日のコ-スは箱根駒ヶ岳のふもとの相模湾が一望できるところです。
もっとも、私には景色を楽しむ余裕は
ほとんどなかったですけれど・・・。
NO.40 10/2 みかん
1年は1月1日より始まるのに、年度は4月から始まる、
学校(日本の)も4月から始まる。
外国では学校は9月から始まるようになっているようです。
何故、一年の始まる日が幾つかに別れているのでしょう?
そこにはどのような意味があるのですか?
NO.41 10/6 山漁師の六太夫
さて、また難問が出されたのでお教え願えませんか?
これは、仕事上で使うのですが、若い子から質問されても、
可能かどうか即答できなかったのでご相談します。
Xの1.8乗を、四則演算と平方根だけで
式に出きるのでしょうか?
1.8は固定の数字です。
ご存じかどうか解りませんが、
シーケンサー(PLC プログ ラマブル コントローラー)で、
機械の制御に使うのですが、演算機能が限定されているらしく、
どれほど長い式になっても大丈夫なのですが、
いかんせん 上記の四則演算と平方根しか
使用できないらしく
(今時の1,000円以下で売っている電卓レベル)、
可能なら式を、
不可能ならその理由が知りたいと思っています。
NO.42 10/11 わたあめ
X の 1.8 乗 が 四則演算とroot計算で出来るかとの事ですが、
一般的には出来ない事は明らかですね。
1.8 の時だけ出来るかというのですが、
root は 2分の1乗 、1.8 は 5分の9乗ですから
5を2でを用いて表すことが必要になりますが、
5と2は素数なので 乗除演算
(分母であるから加減算は出来ない)
のみで表す事は出来ないので「不可能」というのが
答えではないでしょうか?
ただし、 近似計算ならば可能であり、
実業的にはさしつかえありません。
というより、実務面で必要な実数は普通誤差 1 から 0.1%、
特殊な時でも 0.01%です。
実用上は十分なので近似計算値を使うのがあたりまえです。
特殊な現場では場合に応じてその範囲を決めています。
NO.43 10/12 Junko
xの1.8乗について詳しく説明しましょう。
これを有理数表示しますと、1.8=9/5となります。
x>0に対して、指数が有理数の場合m>0ととり、
次のように定義します。
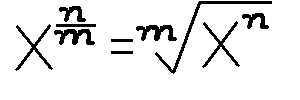
従って、xの1.8乗、つまり9/5乗は、
xを9乗して、5乗根をとればいいわけです。
ところが、ル-ト計算(2乗根)しかできない電卓では、
5乗根は計算できません。
できるのはmが2の何乗かの形にかける時のみということになります。
わたあめさんのご指摘通り、近似計算ならば話は別です。
私はテイラ-展開を利用して近似することを考えました。
テイラ-(Taylor)の定理
f(x)はある区間Iでn回微分可能な関数であるとする。
aはIに属する1つの点とする。
このとき、Iに属する任意のxに対して、xとaとの間にある
適当なξを選べば(ξはギリシア文字でクシ-と読みます。)
f(x)=f(a)+f'(a)(x-a)+f''(a)/2!・(x-a)2+f'''(a)/3!・(x-a)3+ ・・・+f(n-1)(a)/(n-1)!・(x-a)n-1+Rn ①が成り立つ。
f(x)=f(a)+f'(a)(x-a)+f''(a)/2!・(x-a)2+f'''(a)/3!・(x-a)3+ ・・・+f(n-1)(a)/(n-1)!・(x-a)n-1+・・・ ③という無限級数表示が得られます。
そこで0<x<2の時、f(x)=x1.8=x9/5がa=1として、
テイラ-展開できることを示します。
f(x)=x9/5、f(1)=1
f'(x)=9/5・x4/5、f'(1)=9/5
f''(x)=9/5・4/5・x-1/5、f''(1)=9/5・4/5
f'''(x)=9/5・4/5・(-1/5)・x-6/5、f'''(1)=9/5・4/5・(-1/5)
・・・
ですから、
f(x)=1
+9/5・(x-1)
+9/5・4/5・1/2!・(x-1)2
+9/5・4/5・(-1/5)・1/3!・(x-1)3
+9/5・4/5・(-1/5)・(-6/5)・1/4!・(x-1)4
+・・・
+9/5・4/5・(-1/5)・・・((19-5n)/5)・1/(n-1)!・(x-1)n-1
+Rn
となります。Rn=f(n)(ξ)/n!・(x-1)n
=9/5・4/5・(-1/5)・・・((14-5n)/5)ξ(9-5n)/5/n!・(x-1)n
=9/5・4/5・(-1/5)・・・((14-5n)/5)/n!・ξ9/5・ξ-n・(x-1)n
=((14-5・1)/(5・1))・((14-5・2)/(5・2))・((14-5・3)/(5・3))・・・((14-5・n)/(5・n))・ξ9/5・ξ-n・(x-1)n
=(14/5-1)・(14/(5・2)-1)・(14/(5・3)-1)・・・・(14/(5・n)-1)・ξ9/5・(1/ξ)n・(x-1)n
n→∞とした時にRn→0を示します。
まず、0<x-1<1、
ξはxとa(=1)との間の値ですから、
1<ξ<x
0<1/ξ<1
|Rn| =|14/5-1|・|14/(5・2)-1|・|14/(5・3)-1|・・・・|14/(5・n)-1|・|ξ|9/5・|1/ξ|n・|x-1|n
=C・|14/(5・2)-1|・|14/(5・3)-1|・・・・|14/(5・n)-1|・|1/ξ|n・|x-1|n
(ただし、C=|14/5-1|・|ξ|9/5で定数。)
<C・|1/ξ|n・|x-1|n→0 (n→∞)
(n≧2のとき、|14/(5・n)-1|<1なので)
|Rn| =|14/5-1|・|14/(5・2)-1|・|14/(5・3)-1|・・・・|14/(5・n)-1|・|ξ|9/5・|1/ξ|n・|x-1|n
=C・|14/(5・2)-1|・|14/(5・3)-1|・・・・|14/(5・n)-1|・|1/ξ|n・|x-1|n
<C・|(x-1)/ξ|n→0 (n→∞)
この部分については実は未解決(?)なのです。
0<x<1/2のときは、ξの取り方によっては必ずしも
-1<(x-1)/ξとはなりません。
従って、上記のようなやり方では証明できません。
|14/5-1|・|14/(5・2)-1|・|14/(5・3)-1|・・・・|14/(5・n)-1|の部分を抱き込んでいかなければならないのだと思います。 どなたかアドバイス願います。
不完全ながら 0<x<2の時(1/2<x<2についてはいいですよね。)
f(x)=x1.8=x9/5がa=1として、
テイラ-展開できたとして、
f(x)=1
+9/5・(x-1)
+9/5・4/5・1/2!・(x-1)2
+9/5・4/5・(-1/5)・1/3!・(x-1)3
+9/5・4/5・(-1/5)・(-6/5)・1/4!・(x-1)4
+・・・
+9/5・4/5・(-1/5)・・・((19-5n)/5)・1/(n-1)!・(x-1)n-1
+・・・
を計算(加減乗除だけ)することで近似できるわけです。また、2以上のxについては、次のような工夫をします。
x<m5を満たす自然数mを探してきます。
x9/5=(m5・x/m5)9/5 =m9・(x/m5)9/5ここで、x/m5<1なので、 m9を別に計算してかけることでできるわけです。
ただし、このテイラ-展開による近似はx=1の近くでは、
かなり正確な値を求めることができますが、
遠くになると(0や2の近く)誤差が大きいようです。
NO.44 10/13 Junko
xの1.8乗を、四則演算と平方根だけで近似できるかという話です。
root計算ができるということは、
x1/mのmが
2の何乗かの形にかける時だけです。
そこで、1.8を2進数表示すればよいわけです。
1.8を2進数表示する具体的な方法を示します。
1の位は1です。1.8-1=0.8を次に考えます。
少数第1位は、0.8を2倍すると1.6となり、1を越えるので1です。
1.6-1=0.6を次に考えます。
少数第2位は、0.6を2倍すると1.2となり、1を越えるので1です。
1.2-1=0.2を次に考えます。
少数第3位は、0.2を2倍すると0.4となり、1を越えないので0です。
0.4を次に考えます。
少数第4位は、0.4を2倍すると0.8となり、1を越えないので0です。
0.8を次に考えます。
以下同じ様に続けます。
1.8=1.11001100・・・(二)と表示する事ができます。
これは、1.8=1+(1/2)+(1/4)+(1/32)+(1/64)+・・・を意味します。
従って、
x1.8=x1+(1/2)+(1/4)+(1/32)+(1/64)+・・・ =x1・x(1/2)・x(1/4)・x(1/32)・x(1/64)・・・というわけで、これはroot計算とかけ算のみで近似できることになります。
NO.45 10/16 影法師
NO40について
南半球のオーストラリアやニュージーランドでは、
新学期は2月に始まります。
夏休みは12月と1月です。
そうすると、地球上の始まりは、
1月、2月、4月、9月の4通りがあることになります。
本当にどうしてでしょう?
NO.46 10/17 God
私は、愛知県名古屋市に住んでいまして
サラリーマンをしております。
面積を求める問題ですが、
なかなか難しく私の手には負えません。
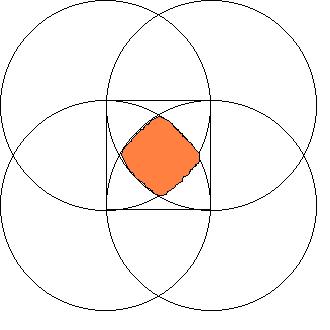
問題:半径Aの円が4つあり、
それが図のように重なっています。
その時、すべての円が重なる
(色が着けてある)部分の面積の求め方は?
NO.47 10/17 Junko
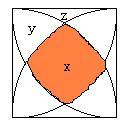
円の半径、つまり中央にある正方形の1辺の長さを
rとします。
下の図のように、それぞれの部分の面積を
x、y、zと設定します。
xを求めればよいわけです。
まず、正方形に注目すると、
r2=x+4y+4z・・・①
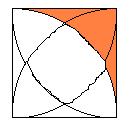
また、下の図のオレンジの部分に注目すると、
正方形から1/4円を差し引けばいいわけですから
r2-πr2/4=y+2z・・・②
また、下の図のオレンジの部分に注目すると、
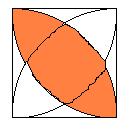
1/4円2つから正方形を差し引けばいいわけですから
(πr2/4)×2-r2=x+2y・・・③
ただし、これは①②から導くこともできます。
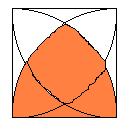
さて、次に下の図のオレンジの部分の面積を具体的に求めてみます。
これは、x+2y+zにあたりますので、これがわかれば③とあわせて、
zの値が求まることになります。
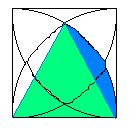
下の図のように補助線を2本ひくと、
緑の正三角形(各辺は円の半径ですから長さはすべてr)と、
青の部分が2つに分けられます。
まず緑の正三角形の面積ですが、
底辺r、高さ(SQR(3)/2)rですから、
(SQR(3)/4)r2となります。
一方、青の部分は1/6の扇形(60゜ですから)の面積から
正三角形の面積をひくことで求められます。
つまり、πr2/6-(SQR(3)/4)r2です。
従って、
x+2y+z=(πr2/6-(SQR(3)/4)r2)×2+(SQR(3)/4)r2
x+2y+z=πr2/3-(SQR(3)/4)r2・・・④
先程書いたように、③④よりzの値を求めることができます。
z=(1-π/6-(SQR(3)/4))r2
これを、②に代入することにより、
y=(-1+π/12-(SQR(3)/2))r2
更にこれを①に代入して、
x=(1+π/3-SQR(3))r2
もっと、すっきりした解答があれば、とも思うのですが・・・。
NO.48 10/22 God
早速の回答ありがとうございました。
なるほど・・・って感じですね。
ところで、ついでにどうですか?
黒塗りの角度を求める問題です。
解いてみてください。
どこかの中学入試問題らしいです。

 戻る
戻る