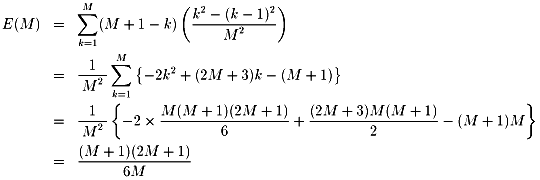
Mが大きくなると、当然得点の期待値E(M)も大きくなることがわかります。
Weekend Mathematics/コロキウム室/1999.4〜6/NO.59
| NO.501 | '99 5/27 | Junko | ダーツの期待値(3) |
一般化して半径M(Mは整数)の円で考えてみました。
つまり中心がOで、半径Mの円板を的として、
同心円上に、半径(M−1),(M−2),…、2,1の円が書いてあります。
得点は小さい円環(一番小さいのは円)から順に、
M点、(M−1)点、(M−2)点、…、最後は1点とします。
得点の期待値をE(M)とします。
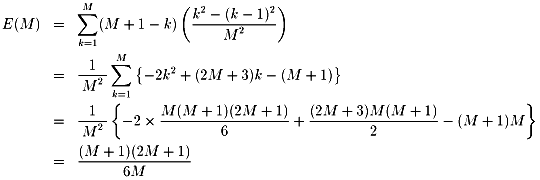
Mが大きくなると、当然得点の期待値E(M)も大きくなることがわかります。
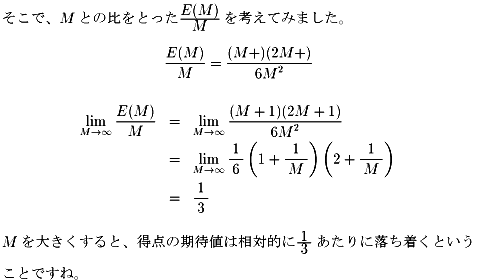
得点の分配と、同心円の区分けをどちらも等差数列(増加の程度が1次的、変な表現ですが・・・?)
で設定していますが、これを変えるとまたおもしろい結果が得られるかもしれませんね。

| NO.502 | '99 5/27 | 数楽者 | 置換積分(10) |
モンテカルロ法は、乱数を用いた手法一般に付けられた名前です。
乱数を用いるとは、ある意味でサイコロを振ることに対応します。
そこで、賭博で有名な場所「モンテカルロ」(F1でも有名です)をとって、
モンテカルロ法と名づけました。(車のレースではないです。)
コロキウムでも紹介されていますが

| NO.503 | '99 5/28 | 浜田 明巳 | 置換積分(11) |
モンテカルロ法についてですが,
πを求めるプログラムはいろいろな言語の解説書に載っています.
今回の大阪府立大学の問題の答を求めるプログラムは次の通りです.
これはQBASICで作ってあります.
QBASICはWINDOWS98や95のシステムCDROMの中の
OLDMSDOSというフォルダの中にあります.
このフォルダの中のファイルをすべてハードディスクにコピーし,
DOSプロンプトを立ち上げ,USモードにして,
QBASICを立ち上げればOKです.
具体的に私の場合だとこうしています.
DOSプロンプトを立ち上げ,
>cd \qbasic (+enter) (QBASICというフォルダの中に収納してあります) >us (+enter) (USモードにします) >qbasic (+enter) (QBASICを立ち上げます)という風にします.終わったら,
>jp (+enter) (日本語モードに戻します) >exit (+enter) (DOSプロンプトから戻ります)です.こんな役立つプログラム言語が98や95に標準装備されている (つまりただで)とは,すばらしい限りです. これは一昔前のQUICK BASICと同じと考えていいでしょう.
'97oosaka.qb SCREEN 12: CLS : RANDOMIZE TIMER kk = 49: xc = 320 + 2 * kk: yc = 200: pi = 3.14159: w = pi / 180 iro0 = 7: iro1 = 2: max = 1000000 DEF fnx (x) = xc + kk * x: DEF fny (y) = yc - kk * y n = 0: k = 0: t1$ = "Press any key to start": t2$ = "Press any key to quit" LINE (fnx(2 * SQR(2)), fny(4))-(fnx(-2 * SQR(2)), fny(-4)), iro0, B PSET (fnx(2), fny(0)), iro1 FOR t = 1 TO 360 LINE -(fnx(3 * COS(t * w) - COS(3 * t * w)), fny(3 * SIN(t * w) - SIN(3 * t * w))), iro1 NEXT: PAINT (fnx(0), fny(0)), iro1 LOCATE 1, 1: PRINT t1$ WHILE INKEY$ = "": WEND: WHILE INKEY$ <> "": WEND LOCATE 1, 1: PRINT SPC(LEN(t1$)); LOCATE 28, 1: PRINT t2$ WHILE n <= max AND INKEY$ = "": n = n + 1 k = k - (POINT(fnx(2 * SQR(2) * (2 * RND - 1)), fny(4 * (2 * RND - 1))) = iro1) s = k / n * 2 * SQR(2) * 2 * 4 * 2 LOCATE 1, 1: PRINT n; "kai shikou" PRINT USING "S=###.###### * pi"; s / pi WEND LOCATE 28, 1: PRINT SPC(LEN(t2$)); : END

| NO.504 | '99 5/30 | 水の流れ | フェルマ−の大定理 (2) |
信頼される国内の某大学院数理科学研究科からのメールによると、
私はワイルズの証明について、それを検討したわけではありませんが、 私の信頼する多くの数学者の意見は、ワイルズにより証明は完結したというもので、 私はそれを疑ってはいません. 証明をフォローした人はたくさんいると思います.ここ数年の「数学」の論説の中に解説があると思いますので、それと参考文献をあわせて読めば理解できると思います.という確かな返事を頂きました。

 E-mail
E-mail
 戻る
戻る