
Weekend Mathematics/コロキウム室/1999.1〜3/NO.44
NO.366 '99 2/25 水の流れ バレンタインデーの贈り物(1)
太郎さんは、バレンタインデーに教え子から贈り物が届きました。
包装紙をはずしてみると、正方形の箱が出てきました。
振ってみてもカタカタ音がしません。
太郎さんは嬉しそうに、ふたを開けてみると、
1辺が10cmの正三角形のチョコレートが現れました。
そこで、太郎さんは正三角形のチョコレートが正方形の箱にカタカタ音が
しないように一体何センチの正方形だったか知りたくなりました。
また、どのように入っていたかも教えてください。
皆さんも、考えてください。
<出 典 :「正方形に内接する正三角形」と題して、
1987年ハンガリーの数学オリンピック出ていたのを改題しました。>

NO.367 '99 2/25 月の光 ゼーター関数物語(17)


NO.368 '99 2/25 水の流れ ゼーター関数物語(18)
「ゼーター関数ζ(2)物語第6夜の始まり、始まり。
昨晩、こんな証明を出しましたね。皆さんは容易に証明できましたね。
『 1+1/4+1/9+1/16+・・・<2 を証明しましょう。』
この結果、一般に数列a(n)について、単調増加で上に有界な数列は
収束しますから、ヤコブは何らかの有限な数に収束することを示しましたが、
ベルヌーイ兄弟にはその和の正確な値を出すことはできませんでした。
ヤコブは”今もって私たちの必死の探求の目をかいくぐっている、
その答えを教えてくれる人があるならば、私たちは多いに感謝する・・・”
と言い訳をしています。
ベルヌーイ兄弟は何もアイデアももっていませんでした。
それどころか、かのライプニッツ
その人さえ明らかに手に負えない問題だったのです。
この級数、1+1/4+1/9+1/16+・・・の正確な和を求める問題は大変
難解で、捕まえどころのない数値を出すためにはベルヌーイ兄弟以上の
天才的能力が必要でした。
面白いことに、この問題は1734年、他でもないヨハン・ベルヌーイのもとで
数学を学んだ一人の若者によって解決されました。
その生徒こそ、偉大なるレオンハルト・オイラーその人でした。
この驚異的な人物は1707年、スイスのバーゼルに生まれました。
当然ながら、幼いときからのその天才ぶりを発揮し、
牧師である父親は息子をあの高名なヨハン・ベル
ヌーイのもとで学べるように奔走したのでした。
1727年、オイラーはロシアのセントペテルスブルグ大学に
医学と生理学のポストに就きました。
その後、1733年、ついにオイラー
にも数学教授の椅子が巡ってきました。
不幸なことに1730年代の中頃から右目の視力が
落ち始め、まもなくまったくみえなくなってしましました。
オイラーがセントペテルスブルグ大学での初年度、
1734年に発表したのがゼーター関数
ζ(2)=1+1/4+1/9+1/16+・・・の値でした。
このとき、彼はこう語っています。
”・・・私は予想もしなかったエレガントな式を発見した。
・・・それもπを用いてのものである。
オイラーの偉大なところは同じ式を2種類の方法で表現して、
結びつけるところにあります。
どこまでも異なる2つの見地から1つの目標を見出していく能力が、
彼の最も深遠で美しい論証を特徴づけています。
さて、ここで、第6夜の問題です。
手始めに、次の無限級数と無限積が等しいことを証明する必要があります。
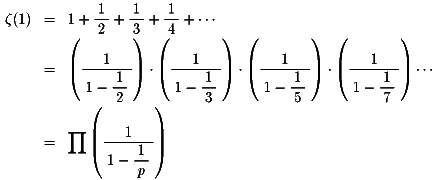
ただし、右辺はすべての素数pにわたる無限積を表します。
この感覚をつけておかないと、随所にでてきます。
今夜はこれで終わりです。ちなみに、上のことが分かった人はNO.359の
「素数の逆数の総和」の証明は容易にできるでしょう。

NO.369 '99 2/25 みや ゼーター関数物語(19)


 E-mail
E-mail
 戻る
戻る