NO.2010 一筆書きの問題(3) 2012.2.12. 迷子の雄猫
以下、A-(3)-Bという記述は、A点からB点へ向かうルートの数が、
その時点で3通りあることを示すものとする。
A-(3)-B-(3)-C-(3)-A-(2)-B-(2)-C-(2)-A-(1)-B-(1)-C-(1)-A
A-(3)-B-(3)-C-(3)-A-(2)-B-(2)-C-(1)-B-(1)-A-(2)-C-(1)-A
A-(3)-B-(3)-C-(3)-A-(2)-B-(1)-A-(2)-C-(2)-B-(1)-C-(1)-A
など、結局はAB間を3回、BC間を3回、CA間を3回通ることになる。
結果、回り方それぞれについて3*3*3*2*2*2*1*1*1通り=216通りの回り方がある。
回り方はa2個、b3個、c3個を同じ文字が隣接しないよう一列に並べる方法と同じであるので、
*a*a****はbcbcかcbcbとb,cの組み合わせで2*2=4通り
*a**a***はbcbかcbcとcbかbcの組み合わせで2*2=4通り
*a***a**はbcbかcbcとcbかbcの組み合わせで2*2=4通り
*a****a*はbcbcかcbcbとb,cの組み合わせで2*2=4通り
**a*a***はbcbかcbcとcbかbcの組み合わせで2*2=4通り
**a**a**はbcかcbとbcかcbとbcかcbの組み合わせで2*2*2=8通り
**a***a*はbcbかcbcとcbかbcの組み合わせで2*2=4通り
***a*a**はbcbかcbcとcbかbcの組み合わせで2*2=4通り
***a**a*はbcbかcbcとcbかbcの組み合わせで2*2=4通り
****a*a*はbcbcかcbcbとb,cの組み合わせで2*2=4通り
合計44通り
よって求めるルートの数は9504通り
#意外に多かった・・。
NO.2009 一筆書きの問題(2) 2012.2.12. 夜ふかしのつらいおじさん
点Aからは6本(偶数)の道が出ているので、Aから出るとAに戻ってきます。
Aから出てAに戻ってくるとき、各点は6本の道があるので、途中Aは2回、Bは3回、Cは3回経由します。
つまり、A4個、B3個、C3個の並べ方を考えればよいことになります。
ただし、両端はAで、途中同じアルファベットが並んではいけません。
AとAの間に入るアルファベットの個数をx,y,z(自然数)とすると、x+y+z=6です。
はじめに、x,y,zにあらかじめ1ずつ割り振って、
x,y,zの3個から重複を許して3個組み合わせる場合の数を数えると、
3H3=5C3=10より、
AとAの間に入るアルファベットの個数のパターンは、次の10通りです。
(1)1,1,4 (2)1,2,3 (3)1,3,2 (4)1,4,1 (5)2,1,3
(6)2,2,2 (7)2,3,1 (8)3,1,2 (9)3,2,1 (10)4,1,1
次にその間にBとCを入れることを考えます。
左右対称になる並び方がないことから、左端のAの右にBがくるものだけを書き出してみます。
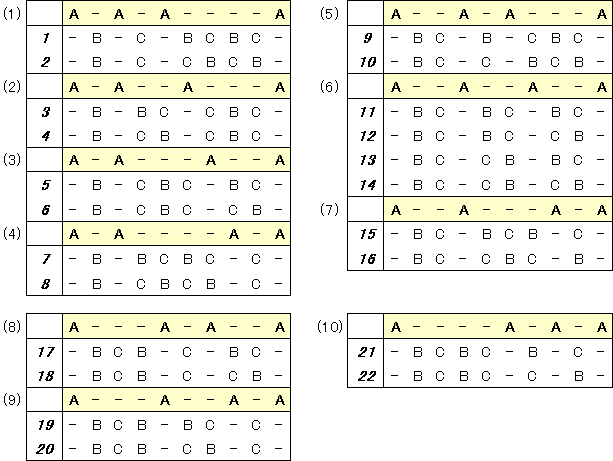
BとCを交換したものを考えると、22×2=44通りになります。
2つの地点の間には3本の道があるので1回目にそこを通るときには3通り、
2回目には2通り、3回目には1通りの方法があります。
以上から、一筆書きの方法は、
44×(3!)3=44×6×6×6=9504通りです。
NO.2008 放物線上の点 2012.2.12. 水の流れ
第270回数学的な応募問題
問題1:
(1)x2 の係数が2である放物線上にx座標が1,2,4である点A,B,Cがある。このとき、三角形ABCの面積を求めよ。
(2)x2 の係数がaで下に凸の放物線上にx座標がα、β、γ(α<β<γ)である点A,B,Cがある。このとき、三角形ABCの面積をa、α、β、γで表せ。
問題2:傾きがmと―mである2直線がある放物線と異なる4点で交わるとき、この4点が同一円周上にあることを証明せよ。
注:この記事に関する投稿の掲載は、2012年2月27日以降とします。
NO.2007 面積の最小(3) 2012.2.12. Ryu1128
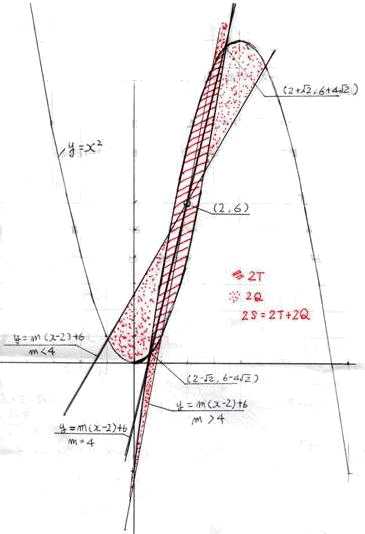
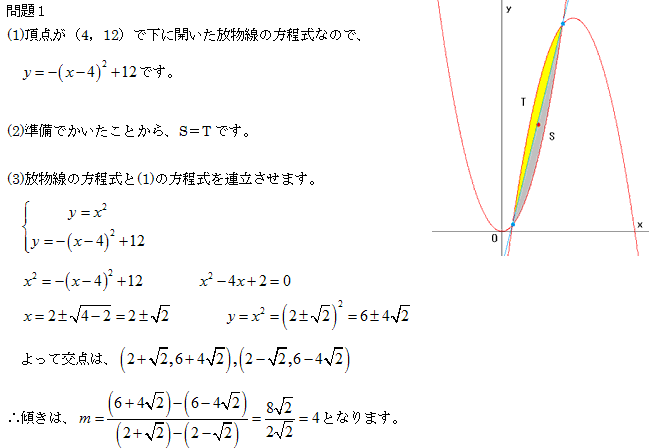
問題1
準備
y=m(x-2)+6 はy-6=m(x-2) と変形できるので、(2,6)を不動点とした直線群です。
(1)y = x2 を y = f(x)とし点対称に移したときの関数を Y = g(X)とします。
座標は次の通りです。
X=(2-x)+2=-x+4 x=-X+4
Y=(6-y)+6=-y+12 y=-Y+12
y=x2 なので
-Y+12 = (-X+4) 2
記号を戻してy= g (x)とし整理すると
y= g (x) = -(4-x) 2+12
これは、(4,12)を頂点とした凸の放物線になります。
(2)y = f(x) とy = g (x)を連立して交点を求めると
(2±√2, 6±4√2)
となります。
交点も当然(2,6)に対して点対象なので準備で述べた直線に乗ります。
(このとき直線はm=4です)
よってTは y = f(x) と y = g (x) で囲まれた部分の1/2となります。
図で示すとおり直線が交点を通らない場合(m≠4)y = f(x)とy = g (x)と直線で囲ま
れる部分をQとし次の関係が成り立ちます。
2S = 2T+2Q
よってS≧Tで等号が成り立つのはQ=0即ちm=4の場合です。
(3)
(2)で述べたとおりSを最小にするmは4です。
m=((6+4√2)- (6-4√2))/(( 2+√2)-(2-√2))=4
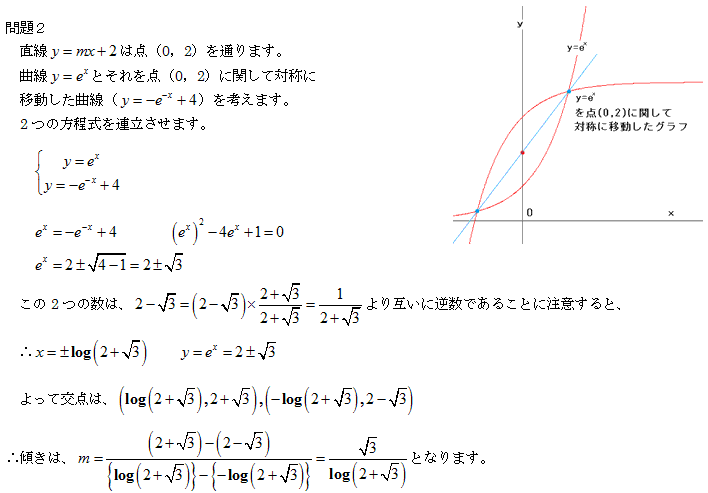
問題2
準備
y=mx+2はy-2=mxと変形できるので、(0,2)を不動点とした直線群です。
問題1と同様の議論が成り立つので
(1)
y = g (x) = -4-e-x
(2)
y = f(x)とy = g (x)を連立して交点を求めると
(ex+e-x)/2=2
coshx=2
x= cosh-12=log(2±√3)
y=2±√3
(3)
Sを最小にするのはy=f(x)とy= g (x)の交点を結ぶ直線であることがわかっているの
で
m= ((2+√3)- (2-√3))/(log( 2+√3)- log(2-√3))=√3/ log( 2+√3)
NO.2006 面積の最小(2) 2012.2.12. 夜ふかしのつらいおじさん
●準備
曲線( y = f(x) )が直線( y = mx + n)で切り取られる部分の面積は、
曲線から直線を引いた式( y = f(x) - (mx + n) )が表す曲線とx軸とが囲む部分の面積(S)と同じです。
つまり、左図の桃色の図形の面積と空色の図形の面積(S)とは同じです。
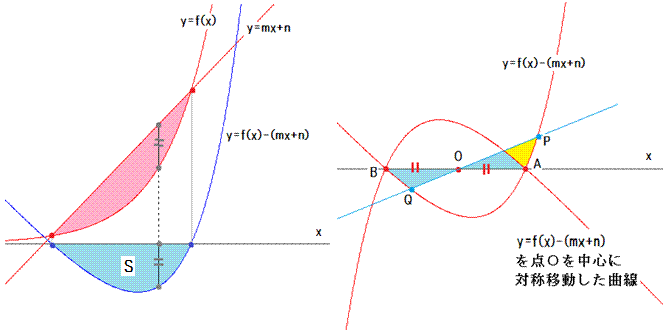
左図の y = f(x) - (mx + n) の曲線がx軸を切り取ってできる弦の中点 O に関して対称に移動すると、
右図のようになります。
弦の中点 O を通る直線が曲線を切り取る部分の面積(S')はSより右図の黄色の部分だけ大きくなります。
S' は、Sに比べ O,B,Q に囲まれた部分(水色)が減り、O,A,Pに囲まれた部分(水色と黄色)が増えます。
水色の部分が、2つの曲線が点 O に関して対称の位置にあるので合同となり面積も等しいからです。
右図で点Oを通る直線が曲線を切りとるとき、水平の場合が面積の最小となります。
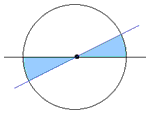
切り取る直線の傾きに関係なく面積が変わらないのは、点対称で閉じた図形の場合です。
分かりやすいのは、円です。
●問題1の普通の解答
この問題の誘導は、とてもすばらしいと思います。
なかなか思いつきません。
まず、誘導がないときの解をかきます。
この方法は放物線のときにしか通用しません。