NO.2005 一筆書きの問題 2012.1.22. スモークマン
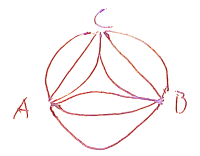
Aから一筆書きのルートは何通り?
ColloquiumNO.278
|
問題1:直線y=m(x−2)+6と放物線y=x2で囲まれた部分の面積Sを最小にするmの値を次の方法で求めよ。
(1)y=x2を点(2,6)に関して対称に移したときの方程式を求めよ。
(2)上の2放物線の交点を通る直線とy=x2で囲まれた部分の面積をTとするとき、SとTの大小を調べよ。
(3)mの値を求めよ。
問題2:直線y=mx+2(m>0)と曲線y=exで 囲まれた部分の面積Sを最小にするmの値を求めよ。
注:この記事に関する投稿の掲載は、2012年2月6日以降とします。
準備

問題1 図のように正四面体をおきます。
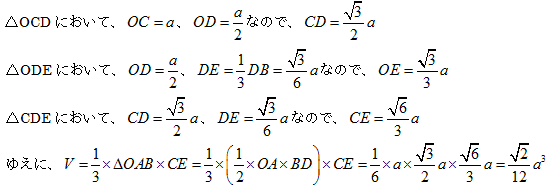
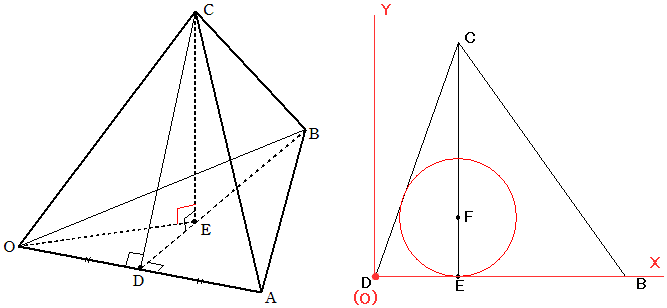
(2) 平面BCDを右の方からみると、正四面体OABCに内接する球は、直線DBとDCに接します。
xy平面上に、△BCDを、点Dが原点、点Bがx軸にのるようにおくと、
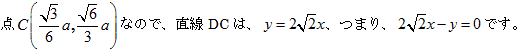


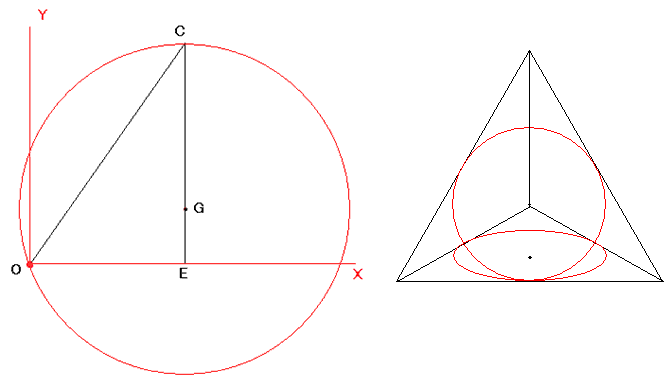
(4) 側面の正三角形に内接する円を底面に正射影するということは、縦方向に3分の1に圧縮するというこ
とです。
図は、正四面体を真上から見たものです。
底面の正三角形に内接する円と側面の正三角形に内接する円をかいています。

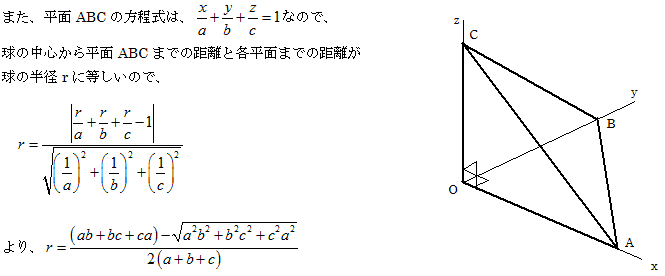
問題2 図のように四面体を空間座標の中に置きます。
(1) 四面体に内接する球がxy平面、yz平面、zx平面に接することから、
内接する球の半径rを用いて、中心は (r,r,r)とおけます。

平面の直線による分割について
平面の分割数=1+(直線の個数)+(交点の個数)が成り立つ。
但し、異なるn本の直線が、同じ共有点を持つとき、交点の個数を1ではなくてn−1個と数える。
件名のような公式を見つけました。
13 + 23 + ・・ + 1003
= 101 C 4 + 4*102 C 4 + 103 C 4
これらの係数はオイラリアン数です。
宇宙人の数学
ア・ラ・カルト編 「07 冪乗と二項係数」 第5節
