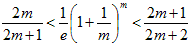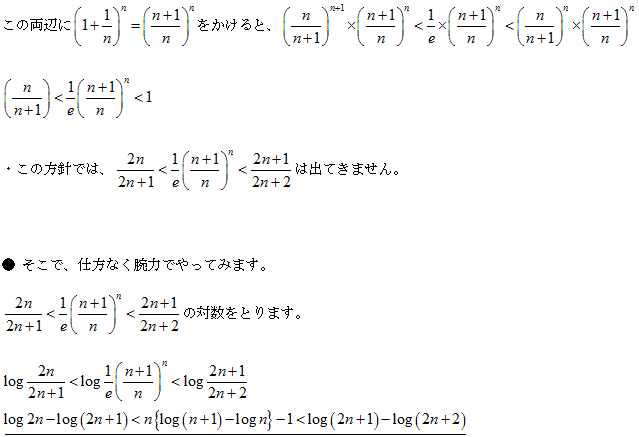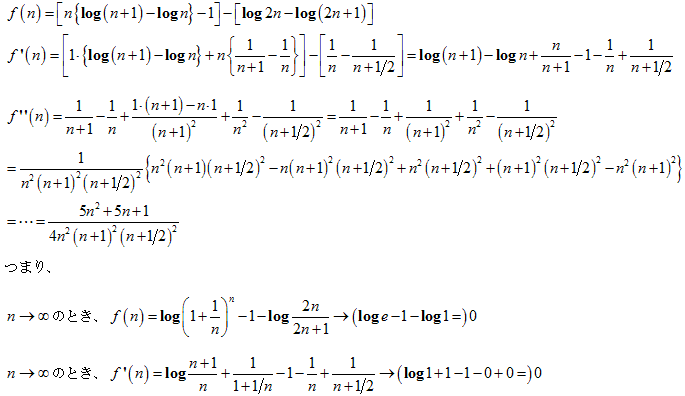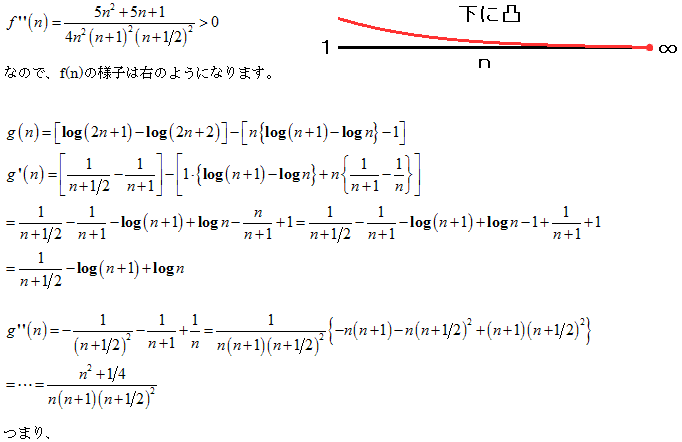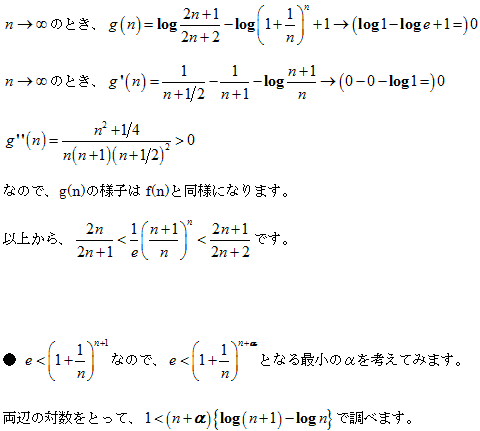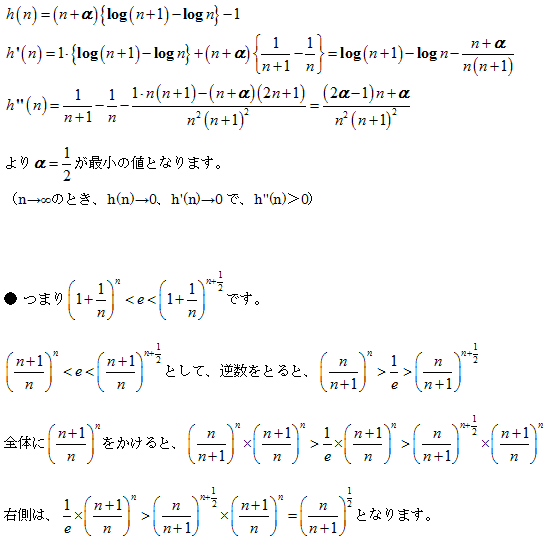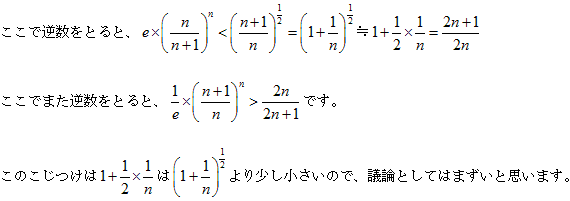NO.2000 四面体の内接球 2011.12.26. 水の流れ
第268回数学的な応募問題
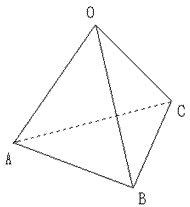
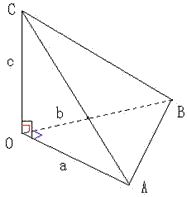
問題1: 一辺の長さがaの正四面体OABCにおいて
(1)正四面体の体積 V をaを用いて表せ。
(2)正四面体に内接する球の半径 r をaを用いて表せ。
(3)正四面体に外接する球の半径 R をaを用いて表せ。
(4)△OABに内接する円の平面ABCへの正射影の面積を求めよ。
問題2:OA=a , OB=b , OC=c で∠AOB=∠BOC==COA=90°
さらに、b=a+cとなる四面体OABCにおいて
(1)四面体に内接する球の半径 r をa、c を用いて表せ。
(2)四面体に外接する球の半径 R をa、c を用いて表せ。
注:この記事に関する投稿の掲載は、2012年1月16日以降とします。
NO.1999 マルファティの円(2) 2011.12.26. 夜ふかしのつらいおじさん
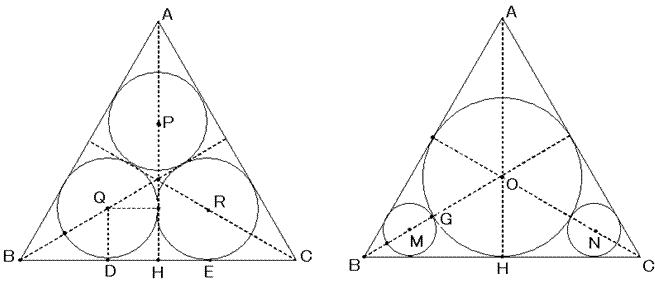
(1)正三角形の1つの内角は60°です。
正三角形の重心、内心、(垂心)、(外心)は同じ点になります。(図のO)
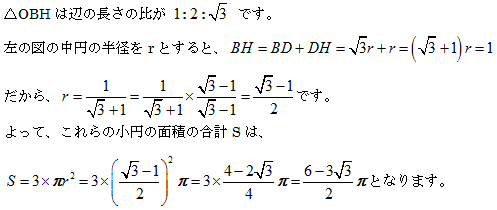
(2)右の図の大円の半径をs、小円の半径をtとすると、
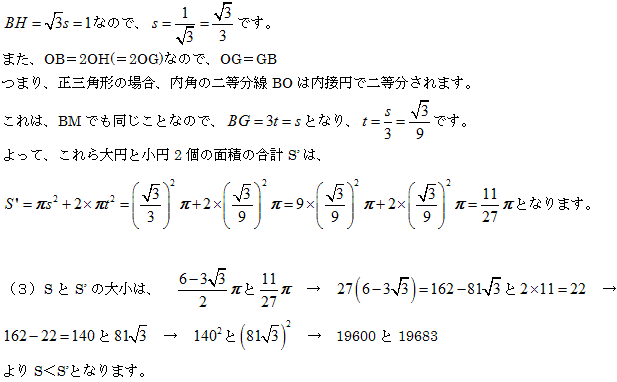
NO.1998 オイラーの多面体定理の拡張(予想)(3) 2011.12.11. 数学マニア
定義の追加修正します。(すいません)
膜を持たない点は、P=要点となる。
膜をもたない辺は、r=小さな輪を持つ。
従って、膜を一つも持たないグラフのときは、
全ての点は、要点になる。したがって、V=P
全ての辺は、小さな輪を持つ。したがって、E=r
そうすると、膜を持たないときは、明らかに成立する。
イメージとして、点が大きくて、小さなリングが引っかかっている。

よって、膜を持たない多角形のサイクルは、点と辺の数が等しくなり
F−E=0、−r+P=0 一致します。
平面と膜は同義ですが、曲線による面もいえるので膜がいいかなと(記号はFですが)
辺の間に全て膜があるとき
V(2)-E(3)+F(3)-C(1)=1,f(1)-r(0)-R(0)+P(0)=1
オイラーの標数は、結局、穴の数(Rではない)によって分類されている。
平面の場合(白いところは、膜がない)

この図で、穴の数(5)から、オイラーの標数を計算すると1−5=−4
定理から、V(16)-E(24)+F(4)-C(0)=-4,予想から、f(4)-r(8)-R(0)+P(0)=-4
となり、それぞれが等しいことが分かります。
空間の場合は、入れ子状態などがあり、複雑になっています。
Aの空洞とBの空洞が独立した空洞(トンネルの入り口のイメージ)
(A空洞からBの空洞に直接、他の空洞に出ないで抜けることができないとき)
Aの空洞とBの空洞が従属した空洞
(A空洞からBの空洞に直接、他の空洞に出ないで抜けることができるとき)
A1空洞とA1も含め最大N個の空洞が従属なとき、その空洞の個数をN−1個とする。
Rは、周りを膜で囲まれている空洞の個数かつ、
各独立な空洞についての、従属な空洞の個数の全ての和とする。
空間の例
立方体を9個並べたものを、上から見た図です。
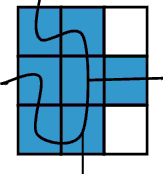
図のように、通ることができるところの膜がないものとします。白いところは胞を持つ
つまり、膜が、10枚減っています。このときR=4−1=3となります。
オイラー数は、V(32)-E(64)+F(32)-C(2)=-2
一方、f(1)-r(0)-R(3)+P(0)=-2となり、一致する。
上の空洞の入り口=A、左をB、下をC、右をDとすると現在4つの入り口がつながって、
つまり従属しているので、4−1=3=R。もし一つ膜がついてBCとADがつながないとき、
独立でそれぞれの数2−1と2−1で合わせて2=Rとなり膜がひとつ増えることとRが一つ減る事が対応しています。
他に、ドーナツ状の空洞も、1サイクルで1個と数えRにカウントします。
単純な場合は、成立すると思いますが、反例があれば、教えてください。
NO.1997 マルファティの円 2011.12.5. 水の流れ
第267回数学的な応募問題
日本実業出版社の「数検の完全対策1〜3級」にあった面白い問題を見つけました。
一辺の長さが2の正三角形の内部に互いに重ならない3個の円を作ります。
(1)3円が互いに外接し、それぞれ2辺ずつに接するとき、これらの円の面積の和を求めなさい。
(2)正三角形の内接円および2辺に接し、内接円に外接する2個の円の面積の和を求め なさい。
(3)(1)と(2)の和はどちらが大きいですか。
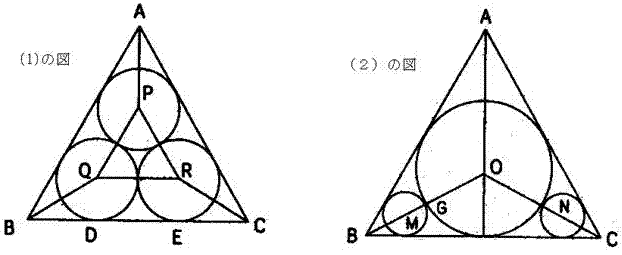
付記:(1)がイタリアの学者であるマルファティの円と言われ、
マルファティ自身は3個の円の面積の和が最大になると1803年に提唱したが,
しかし,安島直円がこの問題を与えその解答を述べたのはマルファティの論文よりも約30年前のことである.
今日ではどのような三角形についてもマルファティの円は最大面積を与えるものではないことが証明されている.
それが(2)のようなときです。
注:この記事に関する投稿の掲載は、2011年12月26日以降とします。
NO.1996 モローの不等式(4) 2011.12.5. DDT
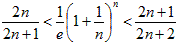 (1)
(1)
(1)をn整数で示せ、という問題なので、n≠0,n≠−1とします。
最初にn>0とします。(1)の最左辺<中辺を移項すると、
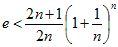 (2)
(2)
となります、(2)の右辺をf(n)とすると、
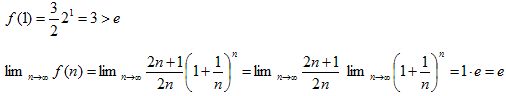
なので、f(n)がnについて単調減少なら、(2)成立です。
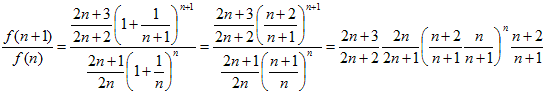
と変形できます。最右辺のn乗の中身は、
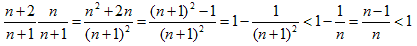
が成り立つので、
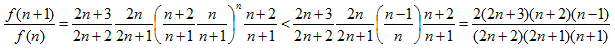 (3)
(3)
です。(3)の最右辺の分子−分母は、
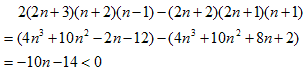
になるので、
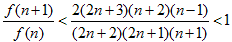
よって、f(n)がnについて単調減少で、(2)成立。
同様に、(1)の中辺<最右辺を移項すると、
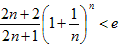 (4)
(4)
になります。(4)の左辺をg(n)とすると、
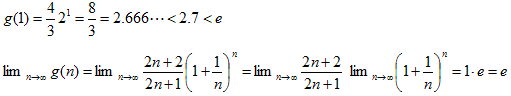
なので、g(n)がnについて単調増加なら、(4)成立です。
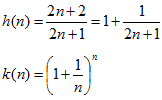
とすれば、g(n)=h(n)k(n)なので、hとkが単調増加なら、gも単調増加です。
h(n)の定義式から、h(n)は明らかに単調増加。
k(n)については2項定理で、
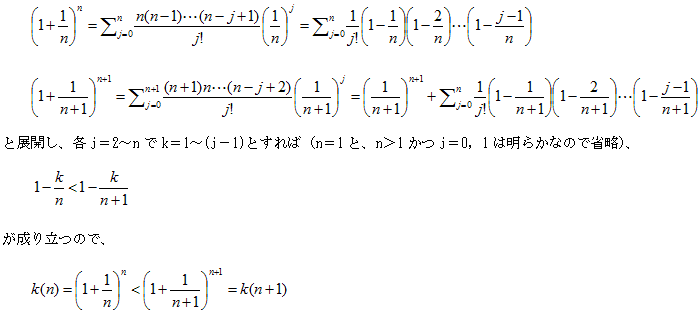
よりk(n)も単調増加。よって(4)成立。(2)と(4)成立なので、n>0について(1)成立。
次にn>−1の場合は、m>1としてn=−mとすれば、(1)は、
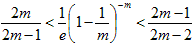
となりますが、m>0として、m→m+1と番号をずらせば、
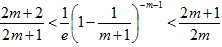
となり、
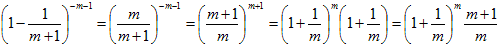
なので、
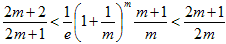
から、
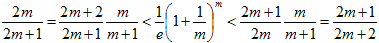 (5)
(5)
を示せば良い事になりますが、m>1の範囲では(1)、
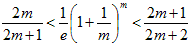
が成り立ち、これは(5)そのものです。従ってn<−1の時も(1)成立。
NO.1995 モローの不等式(3) 2011.12.5. 夜ふかしのつらいおじさん


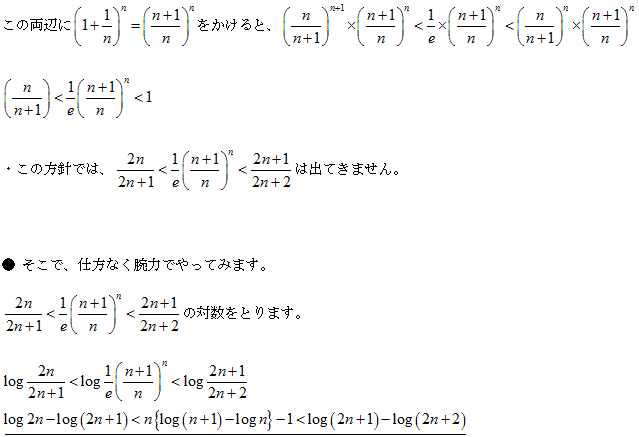
として、下線の式を考えることにします。
nを普通の変数のように考えます。
f(n)=中辺−左辺、g(n)=右辺−中辺として、それぞれが正になるかを調べます。
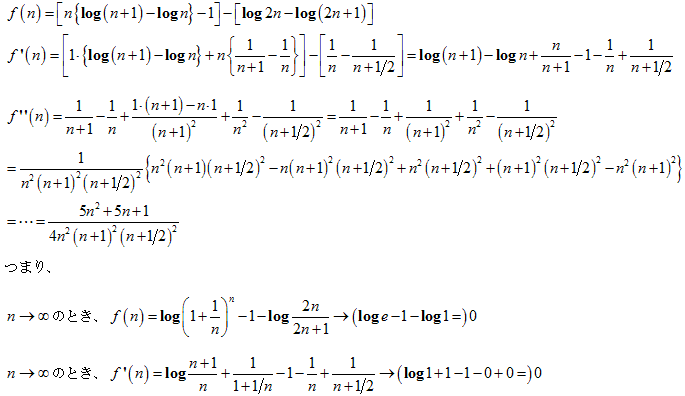
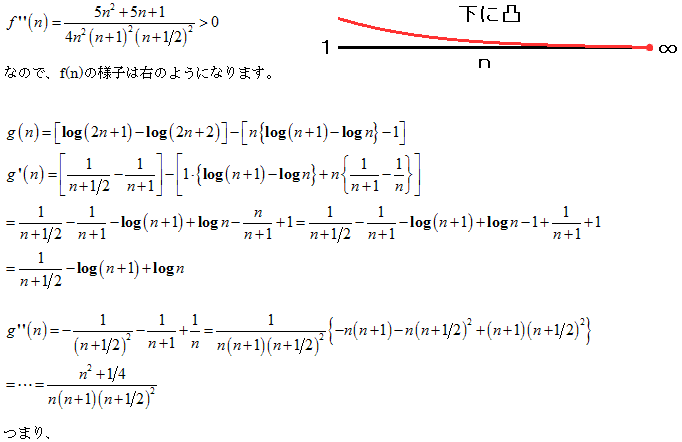
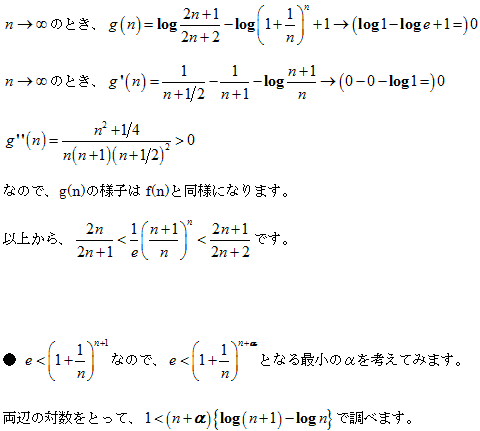
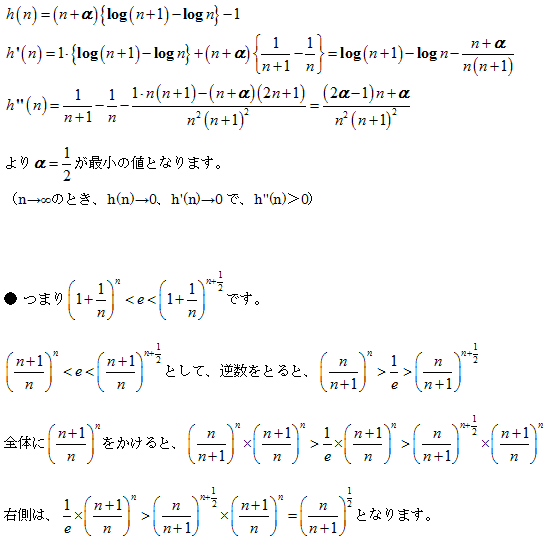
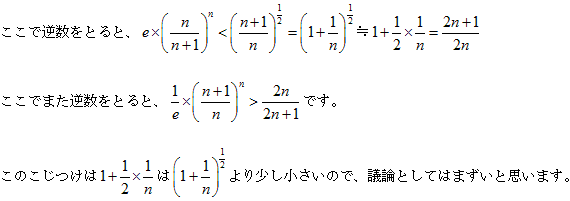
しかし、2nの式を出すのはこんな感覚かなと思います。
NO.1994 モローの不等式(2) 2011.12.5. 浦岡
2n / ( 2n+1 )<( 1/e ) ( 1 + 1/n ) n<( 2n+1 ) / ( 2n+2 ) …☆
2 / ( 2 + 1/n )<( 1/e ) ( 1 + 1/n ) n<( 2 + 1/n ) / ( 2 + 2/n )
1/n = x (0<x<1)とおき、
2 / ( 2+x )<( 1/e ) ( 1+x ) ( 1/x )<( 2+x ) / ( 2+2x )
両辺の自然対数をとり、
log { 2 / ( 2+x ) }<log { ( 1/e ) ( 1+x ) (1/x) }<log { ( 2+x ) / ( 2+2x ) }
log { 2 / ( 2+x ) }<-1 + (1/x) log ( 1+x )<log { ( 2+x ) / ( 2+2x ) }
xlog { 2 / ( 2+x ) }<log ( 1+x ) - x<xlog { ( 2+x ) / ( 2+2x ) } …★
ここで、f(x) = xlog { 2 / ( 2+x ) }, g(x) = log ( 1+x ) - x, h(x) = xlog { ( 2+x ) / ( 2+2x ) }
とおき、不等式★を示す。
f’(x) = log { 2 / ( 2+x ) } - x/( 2+x ), g’(x) = 1/(1+x) - 1,
h’(x) = log { ( 2+x ) / ( 2+2x ) } - x/ ( 1+x ) ( 2+x )
f”(x) = -( x+4 ) / ( 2+x )2, g”(x) = -1 / ( 1+x )2,
h”(x) = -1 / ( 1+x ) ( 2+x ) -1 / ( 1+x )2 + 2 / ( 2+x )2
h”(x) - g”(x) = x / { ( 2+x )2 } ( 1+x )>0,
g”(x) - f”(x) = (x3 + 5x2 +5x ) /
{ ( 1+x )2 }{ ( 2+x )2 }>0 より
f”(x)<g”(x)<h”(x)
また、f’(0) = g’(0) = h’(0) = 0 より f’(x)<g’(x)<h’(x)
さらに、f(0) = g(0) = h(0) = 0 より f(x)<g(x)<h(x) …★
∴所望の不等式☆が成り立つことが示された。



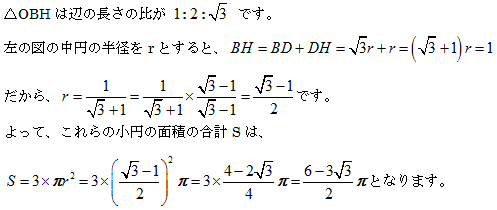
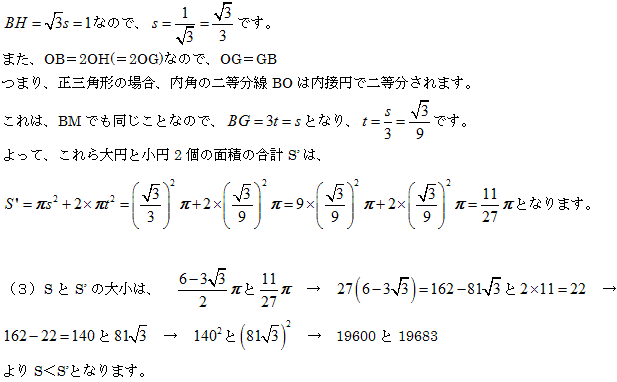





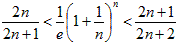 (1)
(1)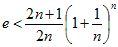 (2)
(2)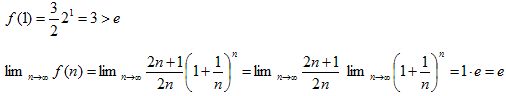
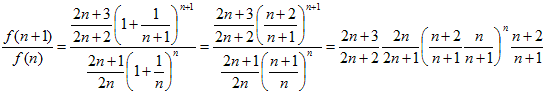
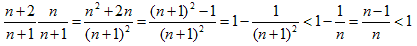
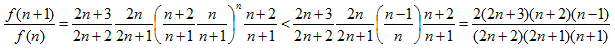 (3)
(3)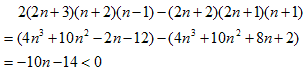
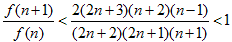
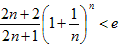 (4)
(4)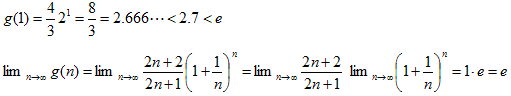
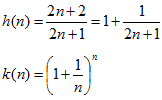
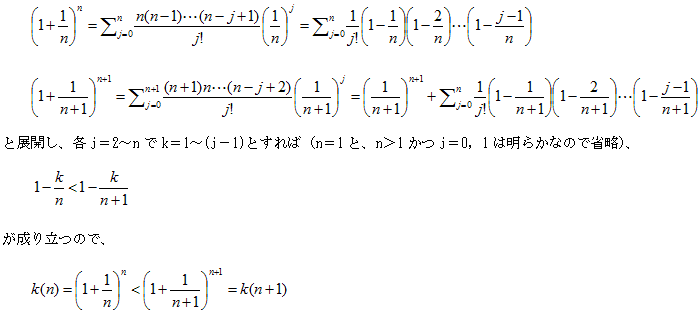
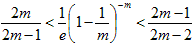
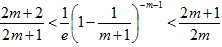
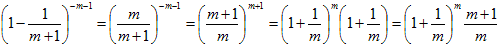
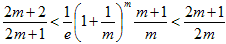
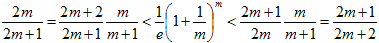 (5)
(5)