NO.1993丂丂丂丂丂僆僀儔乕偺懡柺懱掕棟偺奼挘(梊憐)(2)丂丂丂2011.11.28.丂丂栭傆偐偟偺偮傜偄偍偠偝傫
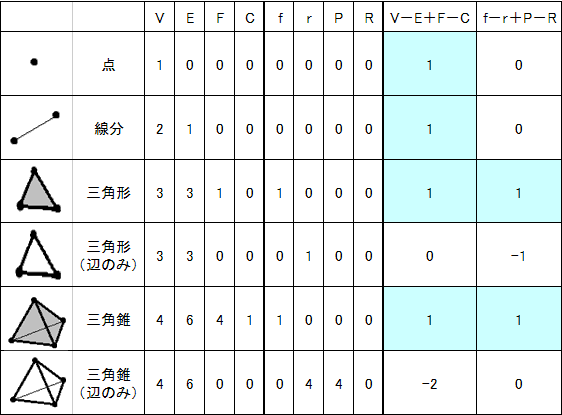
仠倁乮vertex乯丗揰丄俤乮edge乯丗曈丄俥乮face乯丗柺丂偲偟偰
晛捠偺偲傜偊曽偱丄僆僀儔乕偺懡柺懱掕棟乮曈偱楢寢偟偨侾偮偺扨懱偵偮偄偰乯偑丄惉傝棫偭偰偄傑偡丅
暯柺恾宍偺偲偒丄倁2亅俤2亄俥2亖侾丂丂
撌懡柺懱偺偲偒丄倁3亅俤3亄俥3亖俀
乮揧偊帤偼丄倁2摍丗暯柺恾宍丄丂倁3摍丗棫懱恾宍偺偲偒傪帵偟傑偡乯
丂乮暯柺恾宍偺応崌偼丄侾師尦偺慄忬偺応崌傕娷傫偱偄傑偡乯
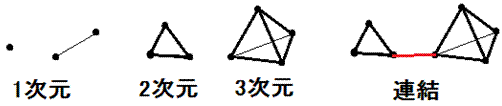
暯柺恾宍偲棫懱懡柺懱偺恾宍傪曈乮E乯偱楢寢偟偰傒傞偲丄 偲傝偁偊偢丄
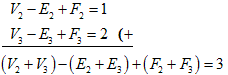
偲側傝傑偡偑丄楢寢偺偨傔偺曈乮俤乯偑侾偮憹偊傞偺偱丄椉曈偐傜侾傪堷偔偲丄
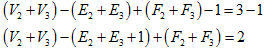
偲側傝丄棫懱恾宍偺幃偼暯柺恾宍偲曈偱楢寢偝傟偰傕惉棫偟傑偡丅
忋偺恾偱偼丄倁亅俤亄俥亖俈亅侾侽亄俆亖俀
師偺恾偺傛偆偵揰乮倁乯傗曈乮俤乯偱暯柺恾宍偲棫懱恾宍偑楢寢偟偰偄偰傕惉棫偟傑偡丅
嵍偺応崌丗倁亅俤亄俥亖俇亅俋亄俆亖俀乮曈偱楢寢偵斾傋丄曈俤偲揰倁偑偲傕偵侾偢偮尭乯
塃偺応崌丗倁亅俤亄俥亖俆亅俉亄俆亖俀乮忋偺応崌偵斾傋丄曈俤偲揰倁偑偲傕偵侾偢偮尭乯

仠暯柺恾宍偲棫懱懡柺懱偺摑崌傪峫偊傑偡丅
丒揥奐恾傪慻傒棫偰偨偲峫偊傞偲丄廳側傝傪峫偊側偗傟偽側傝傑偣傫丅
捀揰倁偼俀尭傝丄曈俤偼俁尭傝傑偡丅
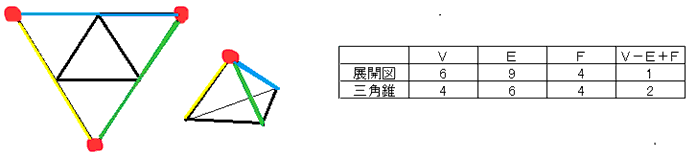
丒曄宍偡傞揥奐恾偱侾偮偺捀揰傪堷偭挘偭偰侾偮柺俥傪壛偊偨偲峫偊偰傕傛偄偲巚偄傑偡丅
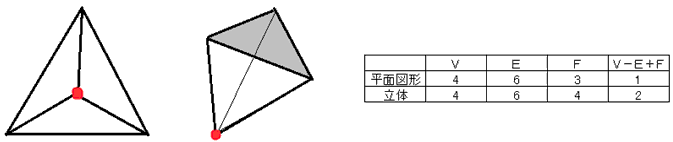
丒暯柺恾宍偲棫懱懡柺懱偺嬫暿偼暵偠偨嬻娫偑偁傞偐側偄偐偺堘偄偱偡丅
偩偐傜丄朎乮暯柺偵埻傑傟偨晹暘乯偺撈棫偟偨屄悢俠傪峫偊傟偽椙偄偲巚偄傑偡丅
丂乮俠偼cell偺僀儊乕僕偐側偲巚偄傑偡乯
丒偙傟偱懳徾偑暯柺恾宍偐棫懱懡柺懱偐傪婥偵偡傞昁梫偑側偔側傝傑偡丅
丒奼挘偟偨僆僀儔乕偺懡柺懱掕棟乮C傪朎偺屄悢偲偟偰乯
丂丂V亅E亄F亅C亖侾ゥゥゥ(*)
仠1990偺暥復偺拞偵
丂丂俠丗朎乮枌偵埻傑傟偨晹暘乯偺撈棫偟偨屄悢
丂丂倖丗楢寢偟偨枌乮揰傑偨偼曈偱椬傝崌偆乯偺撈棫偟偨屄悢
丂丂倰丗彫偝偄椫乮堦偮偺曈偵堦偮偐偗丄偼偢傟側偄乯偺屄悢
丂丂俹丗梫偺揰乮枌傪帩偨側偄俁偮埲忋偺曈偺廤傑偭偨揰乯偺屄悢
丂丂俼丗戝偒側椫乮枌偵埻傑傟偨堦偮偺寠偵堦偮偐偗丄偼偢傟側偄乯偺屄悢
偲偁傝傑偡丅
偦偟偰丄師偺傛偆側椺偑偁傝傑偡丅
丂椺侾丂棫曽懱偺丄忋偲壓偺枌偺傒傪寚偄偨偲偒
丂椺俀丂棫曽懱偺丄忋偲壓偺枌偺傒傪巆偟偨偲偒
丂椺俁丂棫曽懱偺丄椬傝崌偆俁偮偺枌傪巆偟偨偲偒
忋偺恾偼椺侾丄壓偺恾偼椺俁偺偨傔偵偁傝傑偡丅
椺侾偺乽枌乿偼暯柺偲摨媊偩偲巚偄傑偡丅
倖偼乽楢寢偟偨枌乮揰傑偨偼曈偱椬傝崌偆乯偺撈棫偟偨屄悢乿偲偁傝傑偡偑丄
乽楢寢偟偨暯柺偺屄悢乿偲偟偨曽偑暘偐傝傗偡偄偲巚偄傑偡丅
仠忋偺傛偆側偙偲傪峫偊傞偺偼丄侾屄偺楢寢偟偨扨懱傪尒傞偺偵晹暘揑偵堎側傞亀栚亁傪梡偄傞偲偄偆偙偲偱偡丅
丂嘆侾師尦偺栚丗亀曈E偵偦偭偰偟偐擣幆偱偒側偄栚亁
丂嘇俀師尦偺栚丗亀曈E偲柺F偵偦偭偰擣幆偱偒傞栚亁
丂嘊俁師尦偺栚丗亀晛捠偺栚亁
丒俁師尦偺栚偱嶰妏宍傪尒傞偲丄V亅E亄F亅C亖俁亅俁亄侾亅侽亖侾偲側傝丄乮*乯偼惉棫偟偰偄傑偡丅
丒俀師尦偺栚偱嶰妏宍傪尒偰傕丄V亅E亄F亅C亖俁亅俁亄侾亅侽亖侾偲側傝丄乮*乯偼惉棫偟偰偄傑偡丅
丒偲偙傠偑侾師尦偺栚偱尒傞偲丄V亅E亄F亅C亖俁亅俁亄侽亅侽亖侽偲側傝丄乮*乯偼惉棫偟傑偣傫丅
偦偙偱曗惓偺偨傔偵r偑昁梫偵側傝傑偡丅
偟偐偟丄V丄E丄F丄C偼偦偺栚偱尒偰偄傞偺偵丄倰偼俁師尦偺栚偱尒偰偄傞偲偄偆偙偲偵側傝傑偡丅
丂丂V亅E亄F亅C亄倰亖侾ゥゥゥ(**)
仠師偵嶰妏悕傪尒偰傒傑偡丅
丒俁師尦偺栚偱嶰妏悕傪尒傞偲丄V亅E亄F亅C亄倰亖係亅俇亄係亅侾亄侽亖侾偲側傝丄乮**乯偼惉棫偟偰偄傑偡丅
丒俀師尦偺栚偱嶰妏悕傪尒偰傕丄V亅E亄F亅C亄倰亖係亅俇亄係亅侾亄侽亖侾偲側傝丄乮**乯偼惉棫偟偰偄傑偡丅
丂乮俀師尦偺栚偱攇慄偺抣傪挷傋傞偺偼擄偟偄偺偐傕偟傟傑偣傫乯
丒偲偙傠偑侾師尦偺栚偱尒傞偲丄V亅E亄F亅C亄倰亖係亅俇亄侽亅侽亄係亖俀偲側傝丄乮**乯偼惉棫偟傑偣傫丅
仸丂偙偺曽恓偱奼挘偟偰偄偔偺偼擄偟偄偺偱偼側偄偱偟傚偆偐丅
仠丂婎杮揑側恾宍傊偺偁偰偼傔
丂丂V亅E亄F亅C亖倖亅倰亄P亅Rゥゥゥ(***)
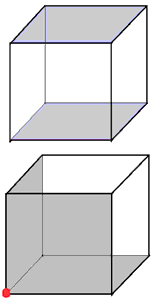
椺偊偽丄師偺傛偆側恾宍偵棙梡偟偰傒傞偲丄悈怓偺晹暘偼偆傑偔偄偭偰偄傑偡丅乮(*)偑惉棫乯
偟偐偟丄悈怓埲奜偼丄(***)偑偆傑偔偄偭偰偄傑偣傫丅