NO.1988�@�@�@�@log2n�̍ő吮���@�@�@�@�@2011.10.24.�@���̗���
���N�̍H�w�@��w������肩����肵�ďo�肵�܂����B
�@
���F���̋L���Ɋւ��铊�e�̌f�ڂ́A2011�N11��14���ȍ~�Ƃ��܂��B
ColloquiumNO.275
|
���N�̍H�w�@��w������肩����肵�ďo�肵�܂����B
�@
���F���̋L���Ɋւ��铊�e�̌f�ڂ́A2011�N11��14���ȍ~�Ƃ��܂��B
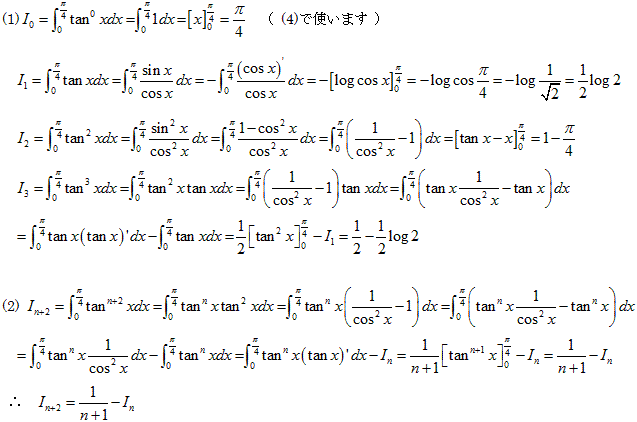
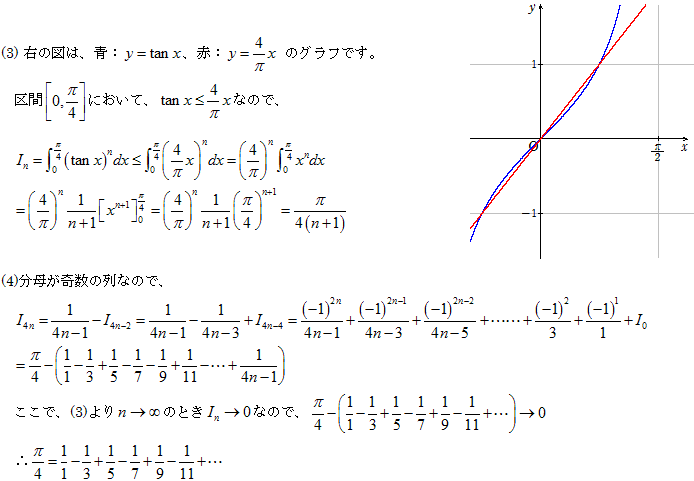
(5)���ʂ������Ă���̂� y=tan -1 x �̃}�N���[�����W�J���l���܂��B
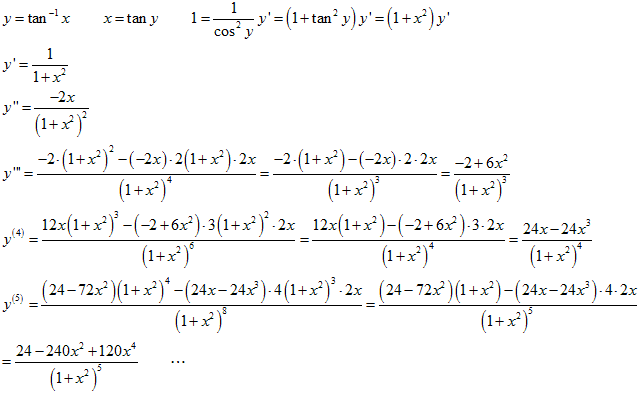
�܂��āA
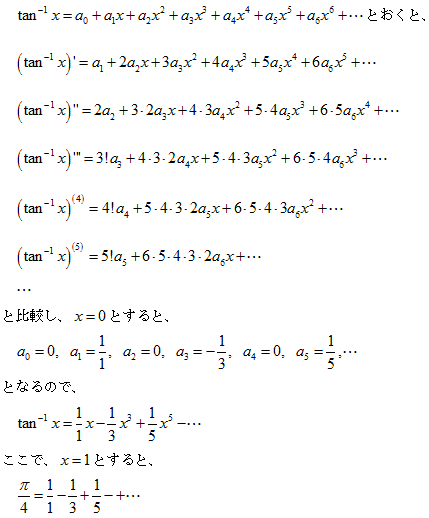
�ƂȂ�悤�ł����A�O���̕����̓����̌v�Z�����ł��B
x��0�Ƃ���̂ŁA�O�������̓����̒萔���̒l�����ŏ\���Ȃ̂ł����A�ȒP�ł͂���܂���B

�@�@�W=�Q�~�S ( ���~�Q���W�ɂ��Ĕ����猩��E�E�̂͂������ɔ����H)
�@
�܂��͂W=|�Q�~�S| (�}�b�`�_���Z������_������)
���ɂ�
�@�@�U�~�Q���P�Q
�@�@�X x �Q���O

�����ŁA�W�J�̌��ʂŌW���̏��������Ɏ��̂悤�ɂ����܂��B

���������� �Ȃ�A�`���a���b���c���d���e���f �͖��炩�ł��B
�����ŁA���������� �Ƃ��܂��B
���̂Ƃ��A�`�C�a�C�b�C�c�C�d�C�e�C�f �̑召���l���܂��B

�ȏォ��A �ƂȂ�܂��B
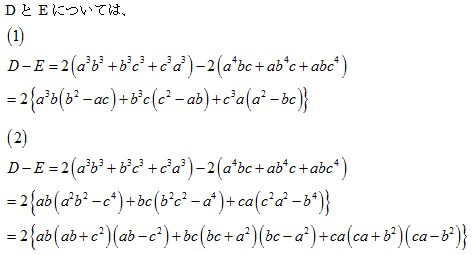
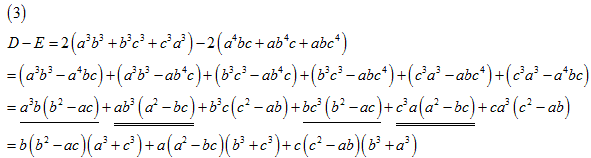
�召�W�̑������l���܂��B
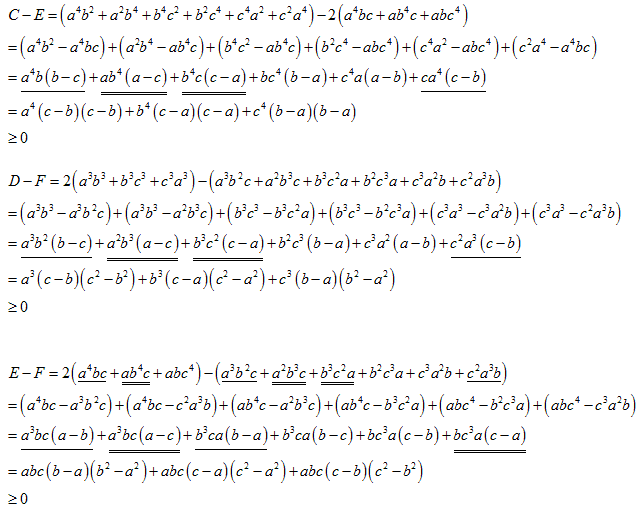
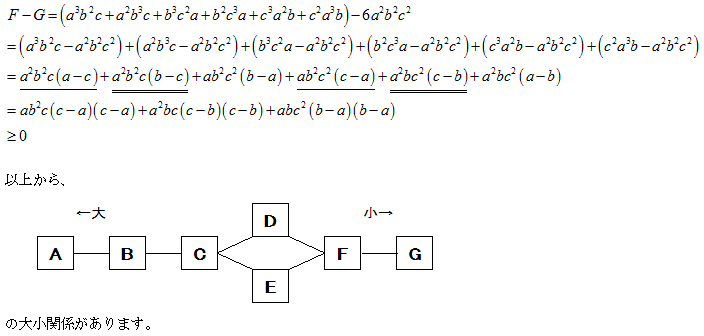
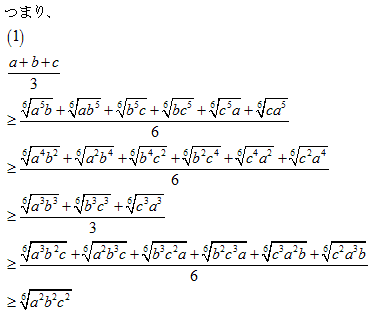

�@�U + �Q = �W
�@�U x �O = �O
�@�T x �Q = �P�O
�F�lK���璸�Ղ������̂ł���
�@�U�~�Q���W
�@�U �� �Q �{ �W
�� ���g������...
�@�W x �Q���R
�@�R x �Q���W
����ɒlj�
�@�O x �Q �� �X
�@�X x �Q �� �X
�@�X x �Q �� �O
�@�U x �R �� �O
�@�U x �R �� �X
�@�U > -�Q-�W
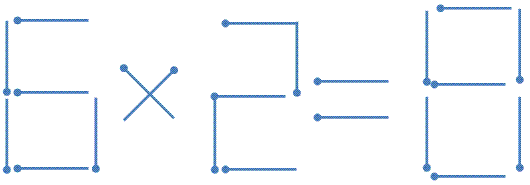
�}�b�`�_���ł��B�Q�{�̃}�b�`���ړ����āA�������藧�悤�ɂ��Ă��������B�i���ł��A���ł��I�j
�R�捪�̂Ƃ�
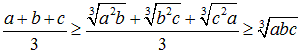
�S�捪�̂Ƃ��A
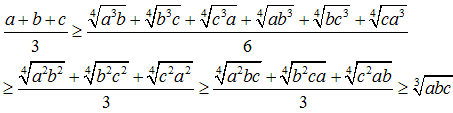
�T�捪�̂Ƃ��A
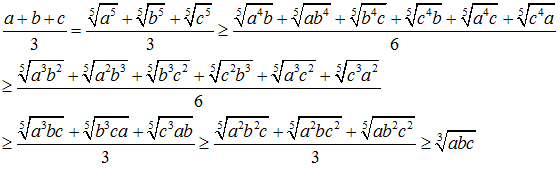
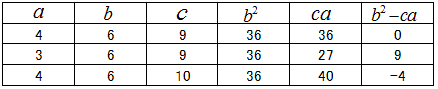
���̕s�����̗�́A
(a+b+c)5�@��W�J���A�Ώ̎����Ƃɕ�����B
�����̕������~���ɕ����āA�s�����̗��B
(5,0,0) (4,1,0) (3,2,0) (3,1,1) (2,2,1)
�����A���̕��@�i�~�p�ɕ��ׂ�j�́A�U���ȏオ�S�����łȂ����ߐ��藧���܂���B
(4,1,1) (3,3,0) �ł͑召�W��܂�Ȃ��B
���[�A�w�b�h�̕s�����̏��������A���藧���܂��B
