NO.1981丂丂丂丂丂丂儔僀僾僯僢僣O儗僑儕乕媺悢丂丂丂2011.9.26.丂悈偺棳傟
僗僐僢僩儔儞僪偺悢妛幰僌儗僑儕乕乮1638乣1675乯偼丄1671擭33嵨偺偲偒丄 栤戣偺摍幃傪敪尒偟偨丅僪僀僣偺執戝側揤嵥悢妛幰儔僀僾僯僢僣乮1646乣1716乯傕丄 傑偨丄摨偠摍幃傪1674擭偵撈椡偱敪尒偟偰偄傞丅崱夞偼偦偺徹柧偱偡丅

拲丗偙偺婰帠偵娭偡傞搳峞偺宖嵹偼丄2011擭10寧24擔埲崀偲偟傑偡丅
ColloquiumNO.274
|
僗僐僢僩儔儞僪偺悢妛幰僌儗僑儕乕乮1638乣1675乯偼丄1671擭33嵨偺偲偒丄 栤戣偺摍幃傪敪尒偟偨丅僪僀僣偺執戝側揤嵥悢妛幰儔僀僾僯僢僣乮1646乣1716乯傕丄 傑偨丄摨偠摍幃傪1674擭偵撈椡偱敪尒偟偰偄傞丅崱夞偼偦偺徹柧偱偡丅

拲丗偙偺婰帠偵娭偡傞搳峞偺宖嵹偼丄2011擭10寧24擔埲崀偲偟傑偡丅
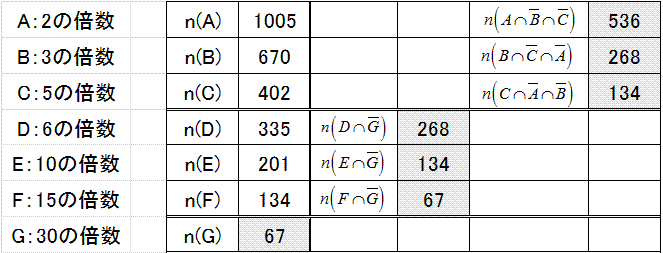
仠壓偺昞偺傛偆偵丄2011傑偱偺偦傟偧傟偺悢偺屄悢傪悢偊傑偡丅
戣堄偺偵傛傝2011埲壓偺崌惉悢偼2011埲壓偺慺悢偲扨埵悢1傪堷偄偰
丂丂2011-305-1 亖1705屄
彫妛惗棳偵峫偊傑偡
2丄3丄5偺攞悢傪寁嶼偟岞攞悢傪堷偗偽2,3,5偵偐偐傞崌惉悢偺屄悢偑寁嶼偱偒傑偡丅
偙傟傪1705偐傜堷偗偽夝摎偵側傝傑偡丅
2011埲壓偵2丄3丄5偺攞悢乮偮傑傝妱傝愗傟傞悢)偼偄偔偮偁傞偐
丂丂
| 2偺攞悢 | 2011/2亖1005+0.5 | 1005屄丒(1) |
| 3偺攞悢 | 2011/3亖670+0.3 | 670屄丒(2) |
| 5偺攞悢 | 2011/5亖402+0.2 | 402屄丒(3) |
| 丂 | 寁2077屄丒(4) |
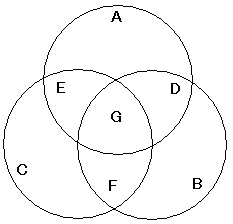
(4)偵偼2,3丒2,5丒3,5偺嫟捠偺攞悢乮岞攞悢)偮傑傝妱傝愗傟傞悢偑娷傑傟傞偺偱 偦偺僟僽偭偨屄悢乮堷偒偡偓偨屄悢)傪丄懌偝側偗傟偽側傝傑偣傫丅 偦偺悢偼壓婰(8)偵側傝傑偡丅
丂丂
| 忋婰偺撪2偲3偺岞攞悢偼丄6偺悢乮2,3,5偑慺悢乯 | 2011/6亖355+0.16 | 335屄丒(5) |
| 忋婰偺撪3偲5偺岞攞悢偼丄15偺攞悢 | 2011/15亖134+0.06 | 134屄丒(6) |
| 忋婰偺撪2偲5偺岞攞悢偼丄10偺攞悢 | 2011/10亖201+0.1 | 201屄丒(7) |
| 丂 | 寁 | 670屄丒(8) |
(8)偱懌偟偨嫟捠偺攞悢乮岞攞悢)偵傕嫟捠偺攞悢乮岞攞悢偺岞攞悢乯娷傑傟傞偺偱偦偺僟僽偭偨屄悢乮懌偟偡偓偨屄悢)傪丄堷偐側偗傟偽側傝傑偣傫丅偦偺悢偼壓婰(9)偵側傝傑偡丅
丂丂
| 忋婰偺撪2偲3偲5偺岞攞悢偼丄30偺攞悢 | 2011/30亖67+0.03 | 67屄丒(9) |
| 2,3,5傪場悢偲偡傞崌惉悢偼 | (4)-(8)+(9) | 1474屄丒(10) |
| 偙傟傪2011埲壓偺崌惉悢1705屄偐傜堷偔偲 | 1705-(10)亖 | 231屄丒丒夞摎 |
仠壓偺昞偺傛偆偵丄2011傑偱偺偦傟偧傟偺悢偺屄悢傪悢偊傑偡丅
傑偢丄慺悢偲弨慺悢偺崌寁偺屄悢偼丄侾偑慺悢偱傕崌惉悢偱傕側偄偙偲偵拲堄偟偰丄
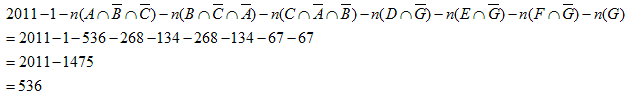
 2011傑偱偺慺悢偑丄305屄偁傞偲偄偆偙偲側偺偱丄
2011傑偱偺慺悢偑丄305屄偁傞偲偄偆偙偲側偺偱丄
丂536亅305亖231偲側傝傑偡丅
堦晹廋惓丂9/26
婏悢揰偑丄侽屄偺偲偒丄慡偰偺揰偐傜堦昅彂偒偑壜擻偱僒僀僋儖傪偮偔傞丅
婏悢揰偑丄俀屄偺偲偒丄婏悢揰偐傜巒傔偰婏悢揰偱廔傢傞堦昅彂偒偑壜擻丅
婏悢揰偑丄俀値屄乮値亜侾乯偺偲偒丄堦昅彂偒偼晄壜擻丅扐偟値夞偱壜擻丅
婏悢揰偑丄婏悢屄偺僌儔僼偼懚嵼偟側偄丅
偙傟傜傪偛専徹偔偩偝偄丅
