NO.1958 五次方程式(3) 2011.7.28. 夜ふかしのつらいおじさん
(1)次のように変形して下線の方程式を解きます。
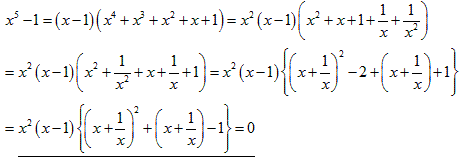
x=0は解ではありません。
x=1 は解です。
2次方程式の解の公式から、
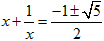
両辺を2x倍すると、
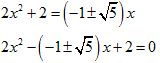
2次方程式の解の公式から、
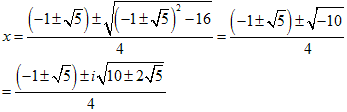
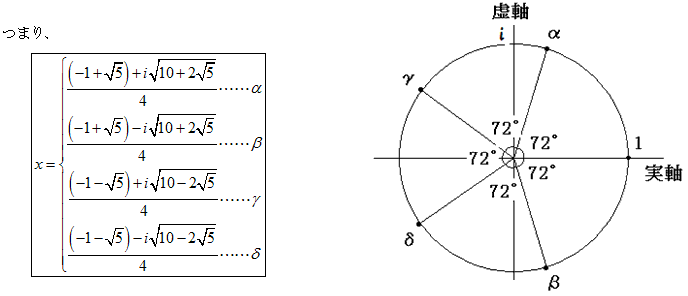
が解です。(αとβ、γとδは互いに共役です)
(2)次のように考えます。
(-x)5-1=0
-x5-1=0
x5+1=0
つまり、(1)の解の(−1)倍が(2)の解なので、
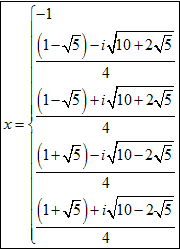
(1)の解とは、複素数平面内で原点対称です。
NO.1957 五次方程式(2) 2011.7.28. 浜田 明巳
1.x5−1=0から,
(x−1)(x4+x3+x2+x+1)=0
∴x=1,または,x4+x3+x2+x+1=0
後半の方程式において,x=0とすると1=0となり矛盾する.
∴x≠0
両辺をx2(≠0)で割ると,
x2+x+1+1/x+1/x2=0
∴(x2+1/x2)+(x+1/x)+1=0………(1)
ここで,t=x+1/xとすると,
t2=x2+2+1/x2
∴x2+1/x2=t2−2
(1)から,
(t2−2)+t+1=0
∴t2+t−1=0
∴t={−1±(1+4)1/2}/2=(−1±51/2)/2
∴x+1/x=(−1±51/2)/2
∴2x2−(−1±51/2)x+2=0
∴x=[(−1±51/2)+{(−1±51/2)2−16}1/2]/4,
[(−1±51/2)−{(−1±51/2)2−16}1/2]/4(複号同順)
∴x={−1±51/2+(1干2・51/2+5−16)1/2}/4,
{−1±51/2−(1干2・51/2+5−16)1/2}/4(複号同順)
∴x={−1±51/2+(−10干2・51/2)1/2}/4,
{−1±51/2−(−10干2・51/2)1/2}/4(複号同順)
∴x={−1+51/2+i(10+2・51/2)1/2}/4,
{−1−51/2+i(10−2・51/2)1/2}/4,
{−1+51/2−i(10+2・51/2)1/2}/4,
{−1−51/2−i(10−2・51/2)1/2}/4
まとめると,
x=1,{−1+51/2±i(10+2・51/2)1/2}/4,
{−1−51/2±i(10−2・51/2)1/2}/4
(参考)方程式
ax3+bx2+bx+a=0(a≠0)
ax4+bx3+cx2+bx+a=0(a≠0)
・・・
は,その昔,相反方程式と呼ばれ,必ずどの問題集にも載っていました.
2.x5+1=0において,t=−xとすると,
(−t)5+1=0
∴t5−1=0
故にtは問題1の方程式の解と一致する.
∴x=−1,{1−51/2±i(10+2・51/2)1/2}/4,
{1+51/2±i(10−2・51/2)1/2}/4
NO.1956 不等式の列 2011.7.28. 数学マニア
不等式の列について考えてみました。他にも列を作る不等式があれば、教えてください。
(1)項数が2個のとき、
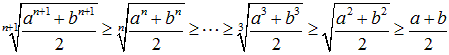
が成り立ちます。
(2)項数が3個以上のときも、同様の不等式の列が存在する。
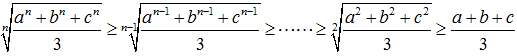
(1) (2)の証明についてお願いします。
(1) の の結果より、簡単に
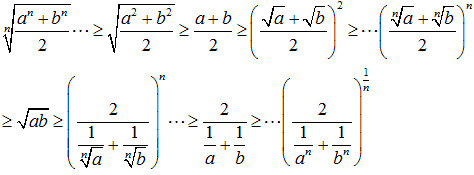
NO.1955 五次方程式 2011.7.25. K.F.
一般の五次方程式が代数的に解けないことはノルウェーの数学者アーベルが証明しました。
ただし、「代数的に」解けないのであって、他の方法で解ける場合もあります。
最も単純な部類の五次方程式の問題です。
次の(1)、(2)の五次方程式を解いてください。
(1) X5−1=0 (2)X5+1=0
NO.1954 カテナリー 2011.7.25. 水の流れ
第261回数学的な応募問題
職場の数学科の先生から(5)の問題を頂きました。
過去問を見ていたら、秋田大学の入試問題(1996年)がありました。興味が持ちましたから、改題して出題します。

注:この記事に関する投稿の掲載は、2011年8月15日以降とします。
NO.1953 ベルヌーイの不等式(2) 2011.7.25. 夜ふかしのつらいおじさん
問題1
tn−nt+(n−1)≧0 の左辺について考えます。
n=2のとき、 t2−2t+1=(t−1)2(1)
n=3のとき、 t3−3t+2=(t−1)2(1t+2)
n=4のとき、 t4−4t+3=(t−1)2(1t2+2t+3)
なので、次のように予想できます。
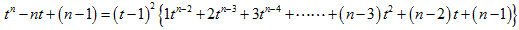
右辺の中括弧{ }の中の各項は、係数と指数の合計が n−1 になっています。
これは、次のように式を展開することで確かめられます。
(t−1)2=t2−2t+1 より
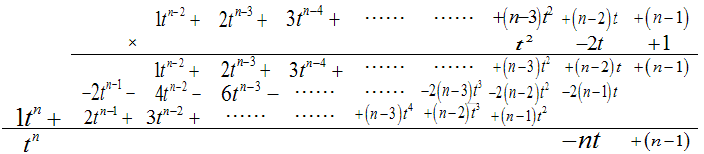
さて、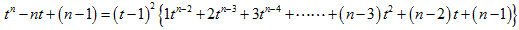 が確かめられました。
が確かめられました。
 右辺について、平方部分は負にはなりません。
右辺について、平方部分は負にはなりません。
また中括弧{ }の中は、t が正なので正です。
よって、証明されました。
tn−nt+(n−1)≧0
この不等式はいろいろな形で表現できますが、
tn≧nt−(n−1)
の形が意味をとりやすいと思います。
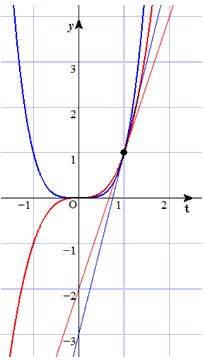
曲線 y=tn の上の点(1, 1)における接線が、
y=nt−(n−1)
ということです。
右の図で
赤は、 y=t3と接線 y=3t−2
青は、 y=t4と接線 y=4t−3
問題2
問題1の式を次のように表すことにします。
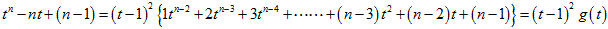
中括弧{ }の部分を とします。
そして、次の形で使います。
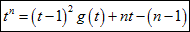
すると、t=4 として、
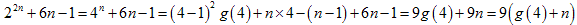
となるので9で割り切れます。
なお、数学的帰納法をためしてみると、
n=1 とすると、(与式) =22×1+6×1-1=9となり、9で割り切れます。
次に、22n+6n-1=9N と仮定すると、( 22n=9N-6n+1 として使います)
n+1 のとき、
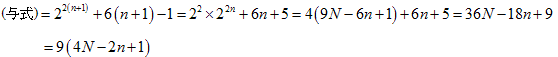
となり、示されます。
問題3
問題2で使った式を使います。
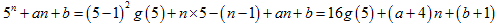
となるので、a+4=16 、b+1=16 なら、この数は16で割り切れます。
つまり、a=12 、b=15 です。
問題4
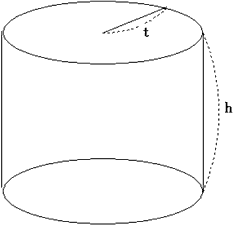 その1
その1
図のように直円柱の底面の半径を t、高さを h とします。
この円柱の体積 V が 2π なので、

さて、表面積Sは、
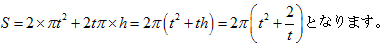
この最小値を考えます。
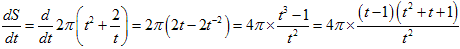
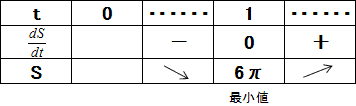
上のような増減表になるので、表面積は 6πが最小値です。
よって、底面積はπ、半径は1です。
その2
次の不等式を使います。
tn≧nt−(n−1) t
等号は、t=1のときです。
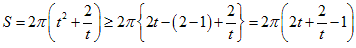
ここで、右辺の括弧( )の中に、相加平均と相乗平均の関係を使います。
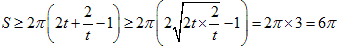
等号は、t=1のときです。
つまり、半径が1になるのでその1と同じ結果になります。
●おまけ
この不等式は n 次を一気に1次にまで引き下げてくれます。
評価を大変楽にしてくれます。

n が自然数ならば、どの項も正であるのは明らかなので、連続する2項の比を調べます。
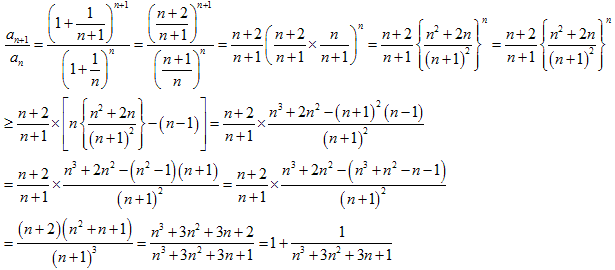
より単調増加と分かります。
NO.1952 相乗平均(3) 2011.7.17. 数学マニア

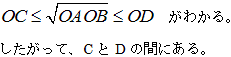
NO.1951 不等式の問題(3) 2011.7.17. 夜ふかしのつらいおじさん
● は正の実数とします。
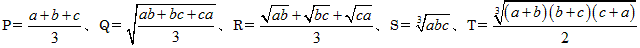
とおきます。
公式の確認をしておきます。
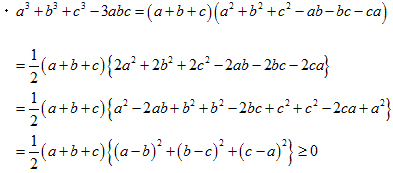
●P≧Qについて
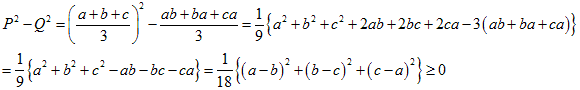
●Q≧Rについて
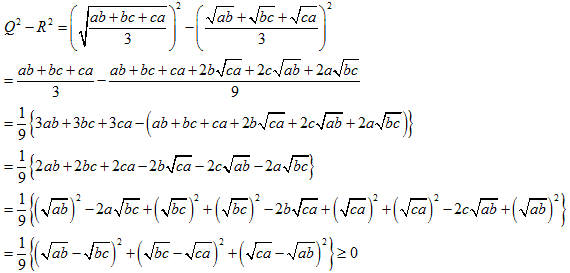
●R≧Sについて(3数の相加平均相乗平均の関係より)
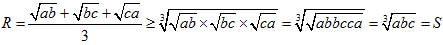
★★以上からP≧Q≧R≧S
つまり、 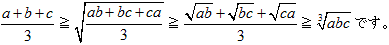
●P≧Tについて
a+b=A,b+c=B,c+a=C とおきます。
すると、(a+b)+(b+c)+(c+a)=2(a+b+c) となります。
よって次の2つの比較をします。
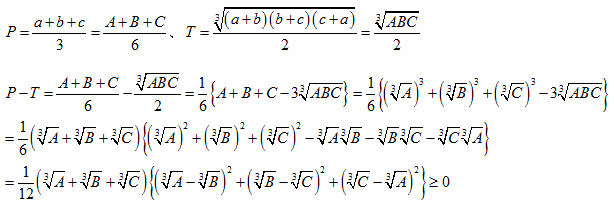
●T≧Qについて。
これは面倒で腕力がいります
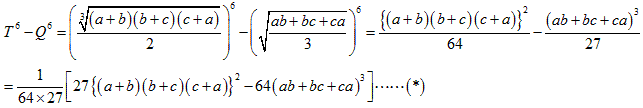
これを f(a,b,c),g(a,b,c),h(a,b,c)を正とし 、(a-b)2f(a,b,c), (b-c)2g(a,b,c),(c-a)2h(a,b,c) の形にしていきます
(*)の大括弧[ ]の中は、展開して、
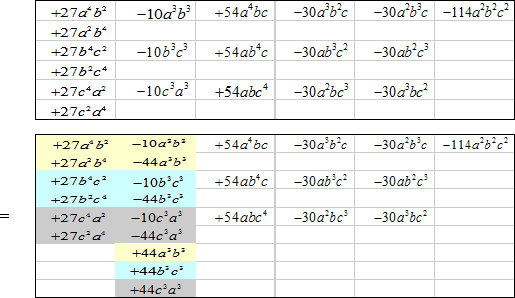
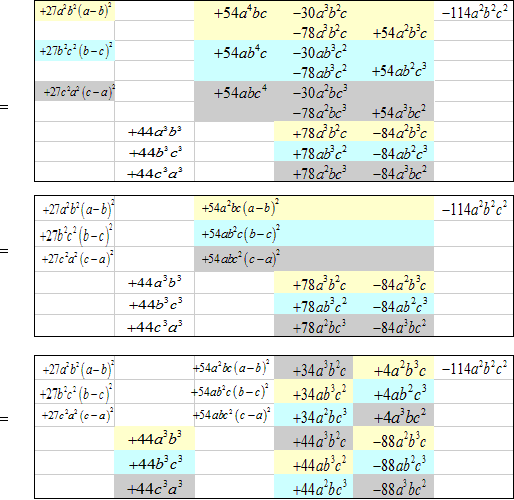
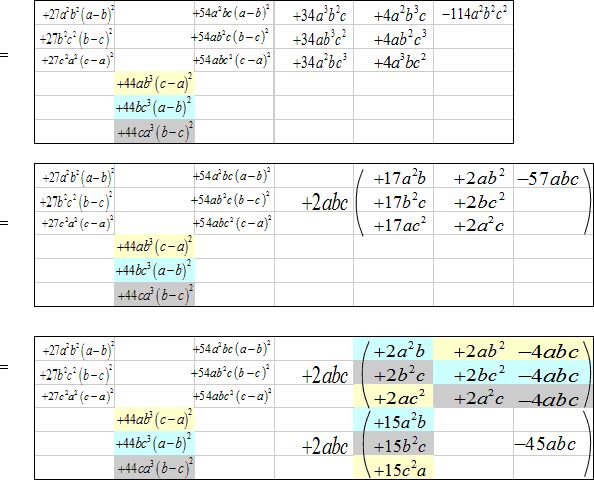
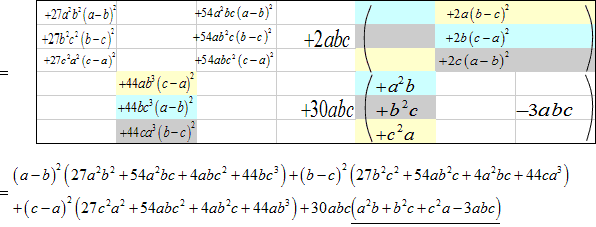
ここで下線部分は、相加平均と相乗平均の関係から、
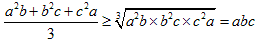
となるので負にはなりません。
以上から、T≧Qがいえました。
★★以上から、P≧T≧Qです。
つまり、 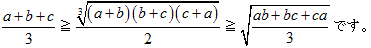
NO.1950 不等式の問題(2) 2011.7.10. スモークマン
一部修正 7/13
考えたことになるのかどうかわからねど...^^;...
以下のように...Orz...
順序だけは…数値計算で…^^;v…
a=1,b=2, c=4
7/3>√((2+8+4)/3)>√5>(3√2+2)/3>2
7>3√(14/3)=6.48...>2+3√2=6.24…>6
3*与式=3*(3*6*5)(1/3)/2=3*90(1/3)/2=6.72…
つまり…
(a+b+c)/3 ≧{(a+b)(b+c)(c+a)}(1/3)/2 ≧√{(ab+bc+ca)/3}≧…
となることがわかる Orz〜
対称式を使って考えるんだろうけど…
たとえば…
(√(a+b)+√(b+c)+√(c+a))/3
数値計算で…(√3+√6+√5)=6.41…
なので…右から3番目になる…^^;v
NO.1949 不等式の問題 2011.7.6. 数学マニア
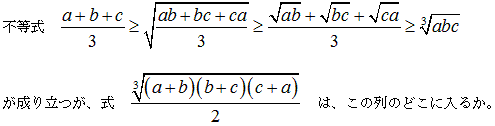
またこのような、式が、他にあれば、教えてください。
NO.1948 ベルヌーイの不等式 2011.7.6. 水の流れ
第260回数学的な応募問題
職場の数学科の先生から生徒が利用している家庭用参考書にある次の質問を受けました。
(それは問題2です)その問題を解くために必要な考えがベルヌーイの不等式です。
問題1
ベルヌーイの不等式 tn−nt+(n−1)≧0
ただし、t>0 ,nは2以上の自然数とする。これを証明せよ。
問題2
nを自然数とするとき、22n+6n−1が9で割りきれることを証明せよ。
ただし、数学的帰納法を用いないでください。
問題3
nを自然数とするとき、5n+an+bが16で割りきれるような16以下の自然数a,bを求めよ。
【出展:1997年一橋大学の入試問題】
問題4
体積が2πの直円柱の中で表面積が最小となる直円柱の底面と半径を求めよ。
【出展:2001年東京女子医科大学の入試問題】
解法として、微分を使った方法、相加平均・相乗平均の利用があります。そして、他の方法でも考えてください。
注:この記事に関する投稿の掲載は、2011年7月25日以降とします。
NO.1947 根軸(2) 2011.7.6. 夜ふかしのつらいおじさん
 問題1
問題1
・直線の決定条件は、
(1)異なる2点(通る2点)
(2)1点と向き(通る点と傾き)
です。
・k についての恒等式 kA+B=0 が満たされる条件は、A=B=0 です。
2円 、x2+y2=1、(x-2)2+(y-3)2=9
は交点を持ちます。
よって、k についての方程式
k(x2+y2-1)+{(x-2)2+(y-3)2-9}=0
のグラフは、2円の交点を通ります。
k=-1 とすると、-4x-6y+5=0
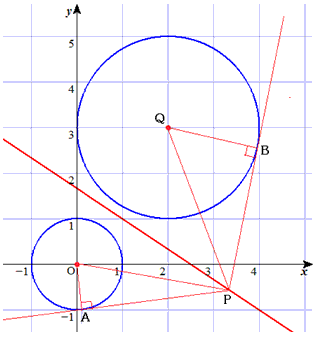 問題2
問題2
図のように2点A、Bをとり、円(2)の中心をQとします。
点Pの座標を (x,y) とすると、
それぞれの直角三角形について、
PA2=OP2−OA2=x2+y2-1
PB2=OP2−OB2=(x-2)2+(y-3)2-4
よって、PA2=PB2 とし整理します。
x2+y2-1=(x-2)2+(y-3)2-4
-2x-3y+5=0

問題3
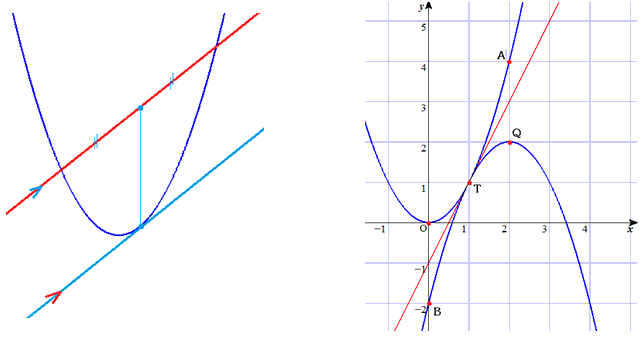
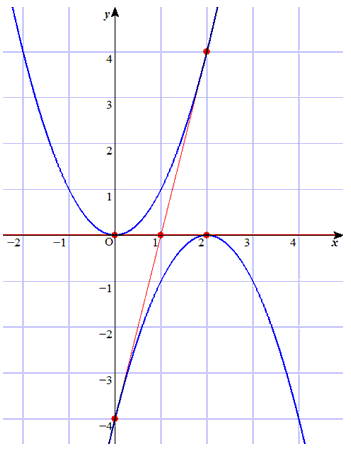
・放物線の形は、x2 の係数で決まります。
( x2の係数の絶対値が等しい2次関数のグラフの形はすべて合同です)
・2次関数のグラフ上の2点の平均変化率は、
その2点の中点から 軸に下した垂線とグラフの交点における微分係数と等しくなります。
以上を頭に置くと、次の図から共通接線は、 y=2x-1です。
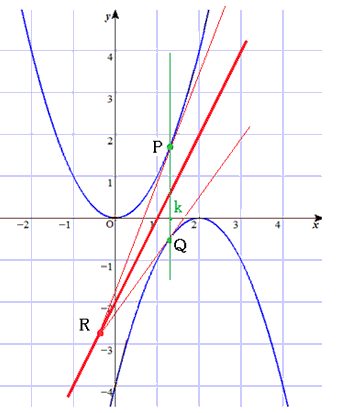
問題5
y=x2・・・(1)
y=-x2+4x-4=-(x-2)2 ・・・(2)
まず、(1)のグラフ上の点A(a,a2) での接線は、
y'=2x より、y-a2=2a(x-a)
整理して、y=2ax-a2 ・・・(3)
次に、(2)のグラフ上の点B(a,-(a-2)2) での接線は、y'=-2(x-2)2 より、
y-{-(a-2)2}=-2(a-2)(x-a)
整理して、y=-2(a-2)x+a2-4 ・・・(4)
(3)、(4)を連立させて、
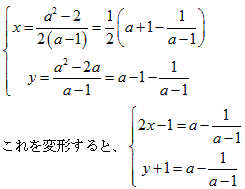
よって、y+1=2x-1 整理して、y=2x-2
・・・・・・・・・・・・・・・・・・・・・・・・
問題4
y=x2・・・(1)
y=-x2+4x-4=-(x-2)2 ・・・(2)
それぞれの点A(a,a2) 、B(b,-(b-2)2) での接線は、
問題5より
y=2ax-a2 ・・・(3)
y=-2(b-2)x+b2-4 ・・・(4)
(3)と(4)との交点Pの座標は、
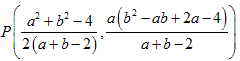
PA=PBなので、
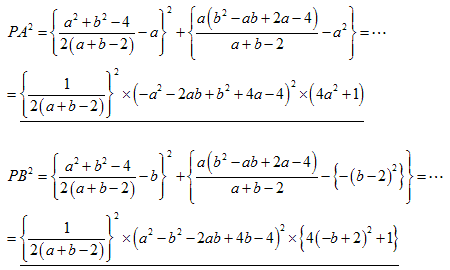
比較して、
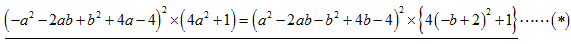
となります。
(*)を満たす、 からなる、
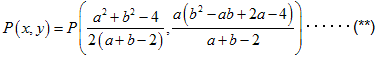 ・・・・・・(**)
・・・・・・(**)
の軌跡が、求めるものです。
この軌跡を求める計算は、簡単ではありません。
aを決め、エクセルの威力を使って、(*)を満たす bの値を求め、x,y を計算してみます。
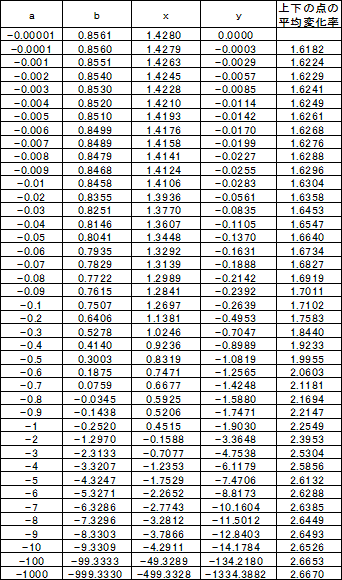
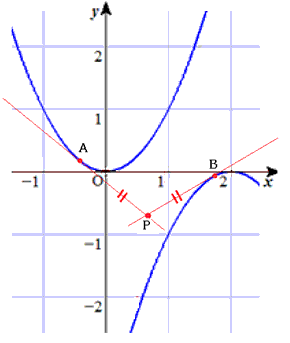
2つの放物線の2点A(a,a2) 、B(b,-(b-2)2) での接線の、
交点P(x,y) の様子を3つ左の図にかきました。
表の点Pをいくつか赤点でプロットし、灰色のスプライン曲線でつないだものが右の図です。
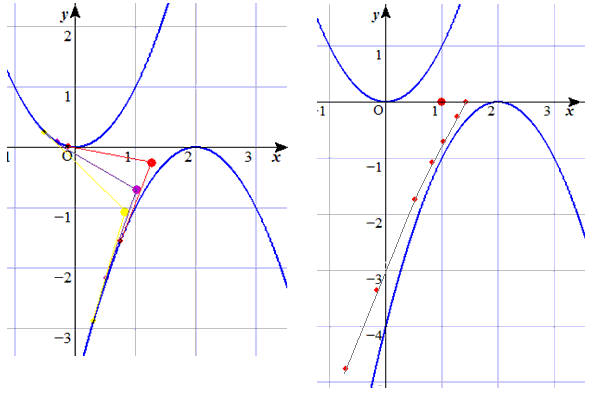
また、点(1,0)に関して点対称な図形も求める軌跡になります。
点(1,0)が題意を満たすのは明らかですが、この方法ではでてきません。
この点は、a=0,b=2 または、a=2,b=0 のときの共通接線で、接点間の中点です。
(**)の式のx や yについて、(a,b)→(0,2) や (a,b)→(2,0)の極限を考えてもでてきません。
問題4について以上です。
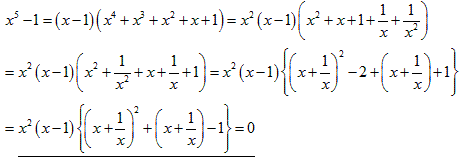
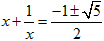
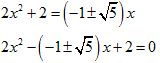
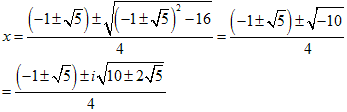
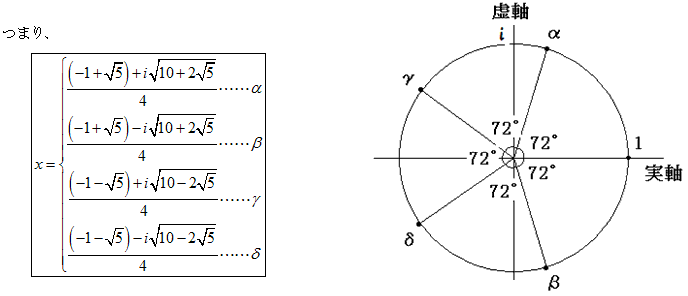
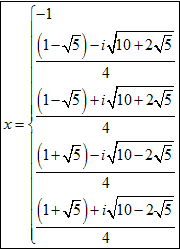
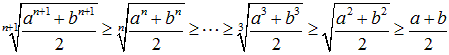
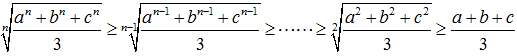
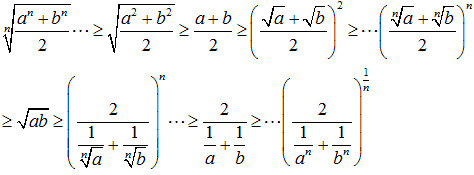

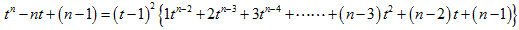
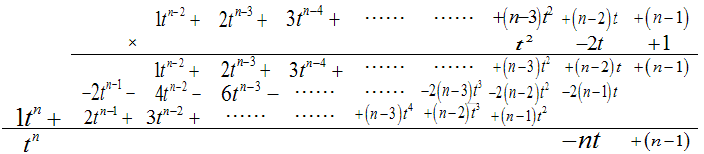
 右辺について、平方部分は負にはなりません。
右辺について、平方部分は負にはなりません。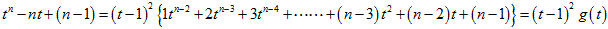
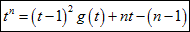
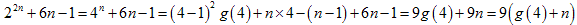
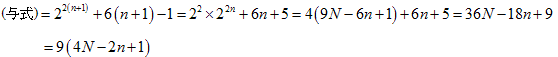
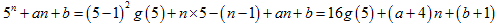
 その1
その1
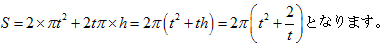
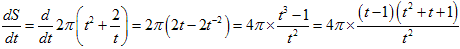

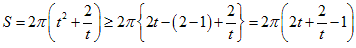
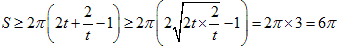

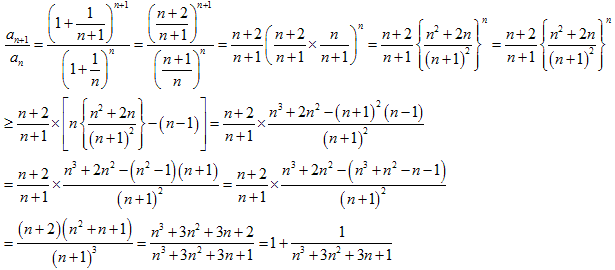
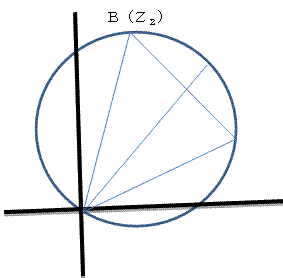

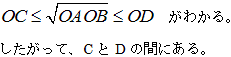
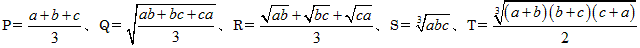
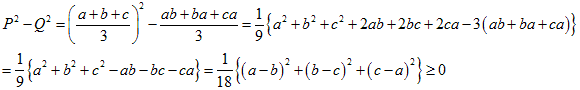
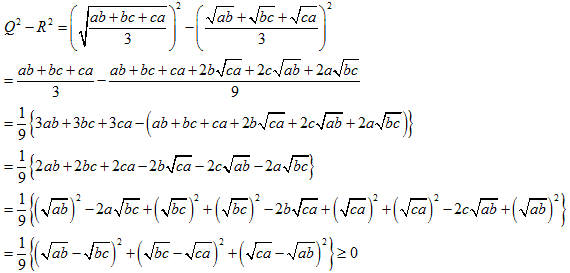
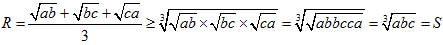
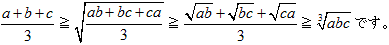
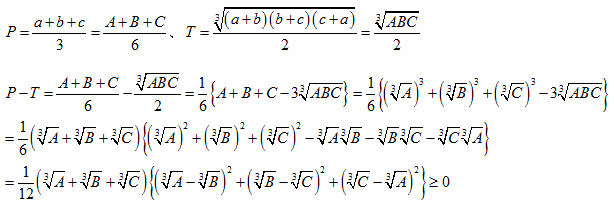
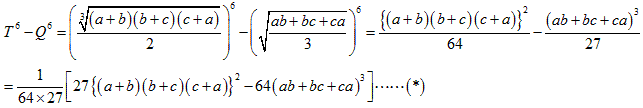




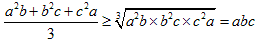
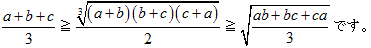
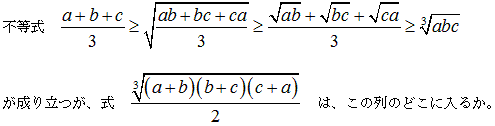
 問題1
問題1 問題2
問題2

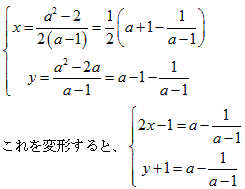

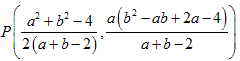
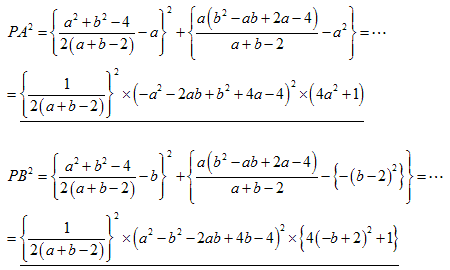
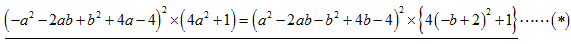
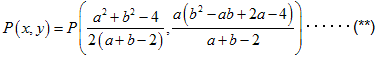 ・・・・・・(**)
・・・・・・(**)


