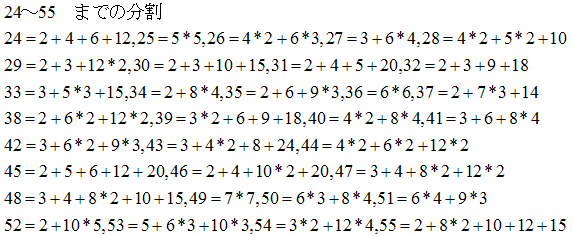NO.1938 行列の変換(2) 2011.5.22. 夜ふかしのつらいおじさん
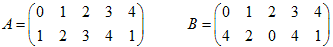
AとBを比べ2行目について、
(1) Aは1が二つ、Bは4が二つです。(互換、(1 4)が必要です)
(2) Aは3があって0がなく、Bは0があって3がないことです。(互換、(0 3)が必要です)
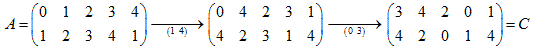
これで、2行目の数がBと同じになりました。
2行目に3がないので、3を使わないような互換でBに近づけます。
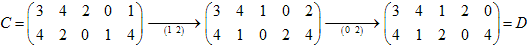
これで上下の組み合わせがBと同じになりました。
あとは列の入れ替えでBにします。
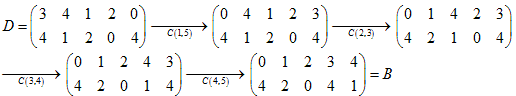
NO.1937 束 2011.5.22. 水の流れ
第258回数学的な応募問題
「大学への数学」のショートプログラムを読んでいたら面白い問題がありました。
紹介します。
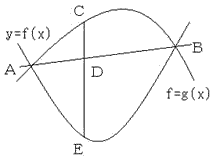
問題1:二次の係数がそれぞれ2、−1の2次関数のグラフを下図のようにそれぞれ
y=f(x)、y=g(x)とする。図でCDEはy軸に平行な線分とする
とき、CD:DE比を求めよ。
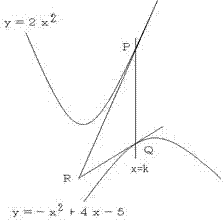
問題2:下図で、y=2x2・・・(1) y=−x2+4x−5・・・(2)と直線x=kの交点を
P,Qとする。Pにおける(1)の接線とQにおける(2)の接線の交点をRとするとき、
Rの軌跡の方程式を求めよ。ただし、軌跡の限界は求めなくて良い。
注:この記事に関する投稿の掲載は、2011年6月13日以降とします。
NO.1936 はさみうちの原理(2) 2011.5.16. 夜ふかしのつらいおじさん
(1)下のグラフを見れば、方程式の解の個数は2k個であることが分かります。
赤: y=x、
青: y=2πsinx (k=1)、緑: y=4πsinx (k=2)、紫:y=6πsinx (k=3)、空色: y=8πsinx (k=4)、
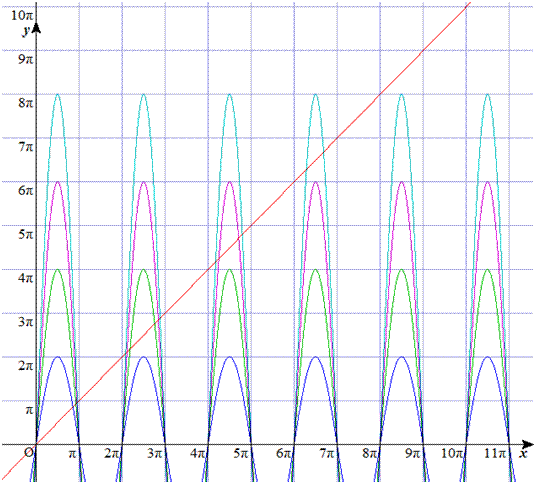
(2) (1)の図をみると、y=2πksinx と y=x のグラフは一つの山で2ヶ所ずつ交わっています。
解を小さい順に xnとすると、i 番目の山では、x2i−1n とx2i の2個の解があります。
この2個は、2π(i−1)=2πi−2π と 2π(i−1)+π=2πi−π の間にあります。
よって、
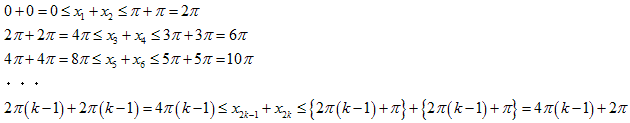
これらの式を辺々加えると、
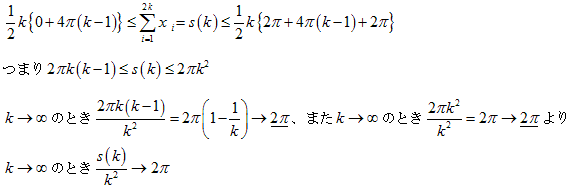
NO.1935 行列の変換 2011.5.5. 数学マニア
以下の数の並びがある。次の条件(1)(2)で、Aの並びをBの並びにしなさい。
(1)横に、上下一緒に交換することができる。
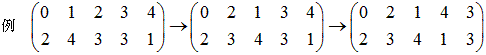
(2)数字を交換することができる。
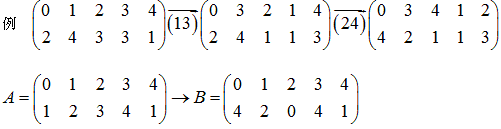
NO.1934 整数の分割(3) 2011.5.5. 数学マニア
23が不可能であることの証明
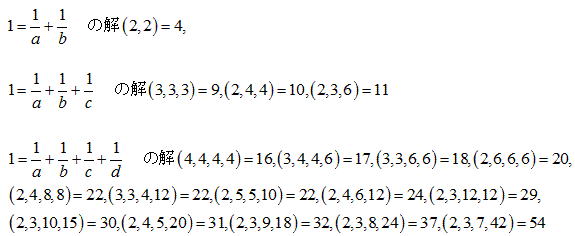
相加相乗平均の不等式から、一般に
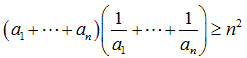 が成り立つので、n が5以上のとき
が成り立つので、n が5以上のとき
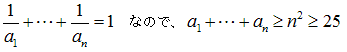 なので、23は不可能です。
なので、23は不可能です。
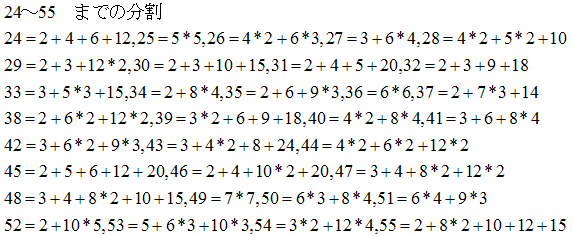
たけちゃんの証明(帰納的に求める方法)完璧な解答です。
分母の和がN(>55)となる解が欲しいとき,
24からN-1までについての解が得られているならば,
Nが偶数のとき,
1/2+(1/2)*(分母の和が(N-2)/2の単位分数の和),
Nが奇数のとき,
1/3+1/6+(1/2)*(分母の和が(N-9)/2の単位分数の和)
「23より大きな数は、適当な分割が存在し、その逆数の和を1にすることができる」
5≦n のとき、n2≦k≦(n+1)2ならば、
k は n 個以下の分割で逆数和を1にすることが可能であることがわかりました。
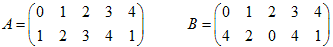
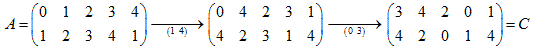
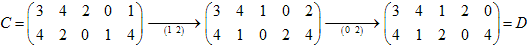
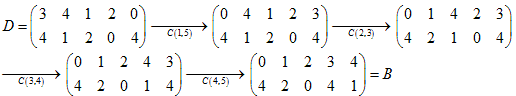



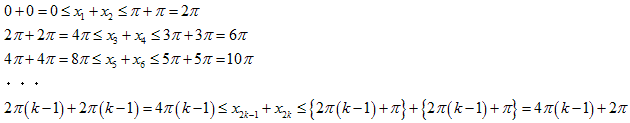
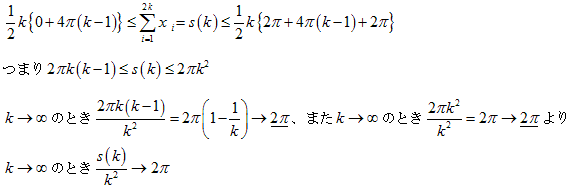
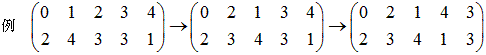
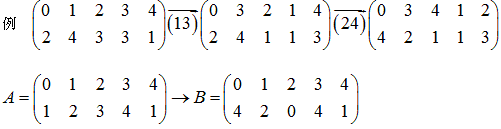
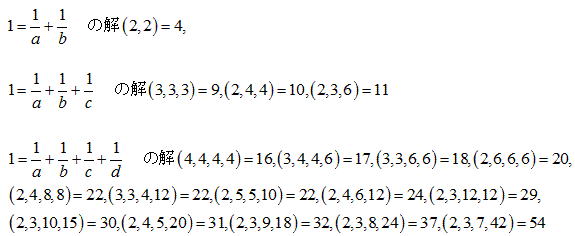
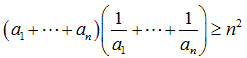 が成り立つので、n が5以上のとき
が成り立つので、n が5以上のとき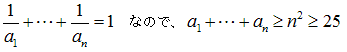 なので、23は不可能です。
なので、23は不可能です。