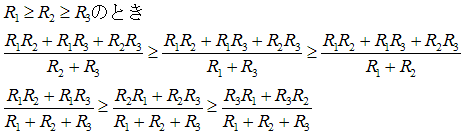NO.1933�@�@�@�@�@�@�͂��݂����̌����@ �@�@�@�@2011.4.25.�@�@���̗���
�ߋ��̑�w������肩��o�肵�܂��B

���F���̋L���Ɋւ��铊�e�̌f�ڂ́A2011�N5��16���ȍ~�Ƃ��܂��B
ColloquiumNO.268
|
�ߋ��̑�w������肩��o�肵�܂��B

���F���̋L���Ɋւ��铊�e�̌f�ڂ́A2011�N5��16���ȍ~�Ƃ��܂��B
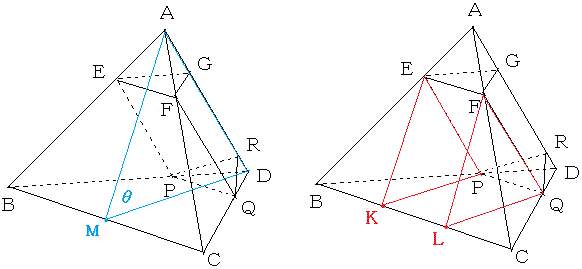
���}�̂悤�ɕ�BC�̒��_��M�A3��������_���AK�AL�Ƃ��܂��B
�܂��A��AMD���ƂƂ��܂��B
�E�}�̂悤�ɐԐF�̕⏕���������ƁA��EFQP�Ő����钸�_�`���܂܂Ȃ����̕����́A
�O�p��EKP-FLQ��2�̎O�p��EBKP�AFLCQ�ɕ�����܂��B
����2�̎O�p���́A��EKP��FLQ���҂�����d�Ȃ�悤�ɕ��s�ړ�����ƁA���l�ʑ̂ɂȂ�܂��B
���̐��l�ʑ̂������l�ʑ��Ƃ������Ƃɂ��܂��B
�����l�ʑ��̕ӂ̒����͂��Ƃ̐��l�ʑ�ABCD��2�^3�ł��B
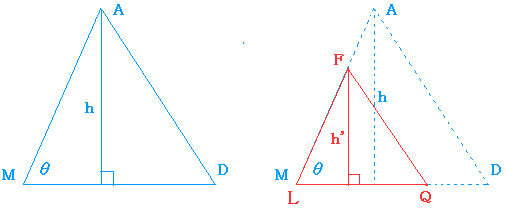
����MAD�Ɓ�LFQ�ɂ��Ē��ׂ܂��B
MD���ӂƂ����Ƃ��̍�����h�Ƃ��܂��B
�@�@�@
�w�����̌����̕����̒l�́A
�@�@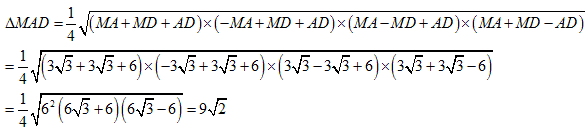
����āA
�@�@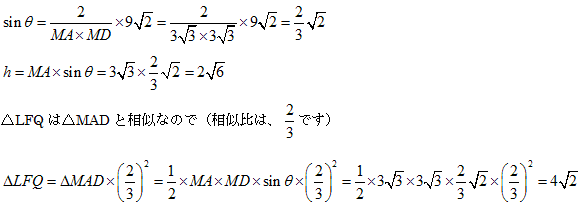
���O�p��EKP-FLQ�������l�ʑ��ɂ��Ē��ׂ܂��B
�O�p��EKP-FLQ�̑̐ς�V1�Ƃ���ƁA
�@�@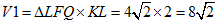
���l�ʑ�ABCD�̑̐ς�V�Ƃ���ƁA
�@�@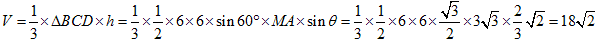
�����l�ʑ��̕ӂ̒����͂��Ƃ̐��l�ʑ�ABCD��2�^3�ł��B
����Ē����l�ʑ̖̂ʐς�V2�Ƃ���ƁA
�@�@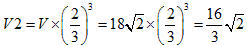
���ȏォ�狁�߂�̐�V3�́A���Ƃ̐��l�ʑ́iV�j����
�O�p��EKP-FLQ�iV1�j�ƒ����l�ʑ́iV2�j�������āA
�@�@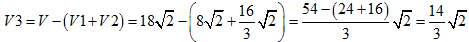
�����ɕ�AB���P�F(x�|1)�ɕ�����_��E�Ƃ��܂��B
�i���̂Ƃ�������l�ł��j
�i��AB�͔�ł�����1�{(x�|1)��x�ɓ�����܂��j
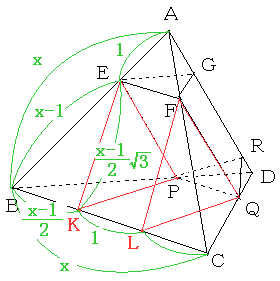
�i�ΐF�́A���ۂ̒����ł͂Ȃ��A��AB��x�Ƃ����Ƃ��̔�̒l�j
���O�p��EKP-FLQ�̐ςׂ܂��B
�@�@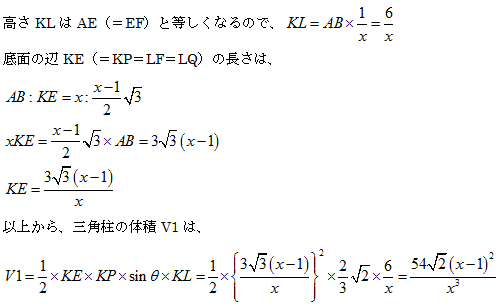
�ȏォ��A�O�p���̑̐�V1�́A
�@�@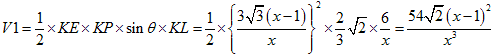
�������l�ʑ��̑̐�V2�́A
�@�@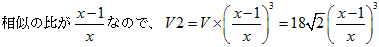
������āA�����^�̑̐�T�́A
�@�@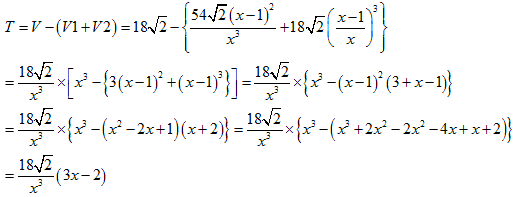
�䂦�ɁA
�@�@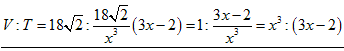
���O���̖��́Ax��3�̏ꍇ�ł��B
�@�@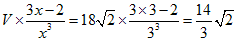
�̂悤�ɁA�͂��߂̖��̓����ƈ�v���܂��B
�i�Q�j�ɂ��čl���܂��B
�� a,b �𐳂̐����Ƃ��Aa��b �Ƃ��܂��B
����̘a��������2�̒P�ʕ����̘a���l���܂��B
���̂Ƃ��Aab�@���@(a-1)(b+1) �ł��B
�@�@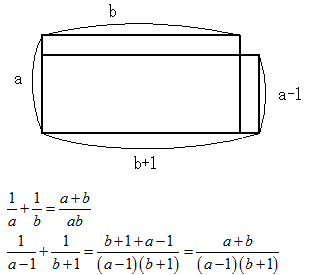
����āA���̌��ʂ܂��B
�@�@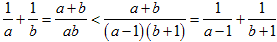
�܂�A�����2���̍����傫��2�̕����̘a�̕����傫���Ƃ������Ƃł��B
�i�����2���̍���������2�̕����̘a�̕����������j
���a��23�ɂȂ�悤��2�ȏ�̐����̑g�ݍ��킹���l���܂��B
���̍ہA�����Ȃ�ׂ����낦�܂��B�i���ʓ��͍���傫���������́j
(1) 11�{12�A�i2�{21�j�@�@�@(2) 7�{8�{8�A�@�@�@(3) 5�{6�{6�{6�@�@�@(4) 4�{4�{5�{5�{5
(5) 3�{4�{4�{4�{4�{4�@�@�@(6) 3�{3�{3�{3�{3�{4�{4�@�@�@(7) 2�{3�{3�{3�{3�{3�{3�{3
(8) 2�{2�{2�{2�{3�{3�{3�{3�{3�@�@�@(9) 2�{2�{2�{2�{2�{2�{2�{3�{3�{3
(10) 2�{2�{2�{2�{2�{2�{2�{2�{2�{2�{3
�E(4)����(10)�̏ꍇ�́A
�@�@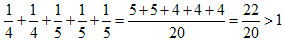
�̂悤�ɁA�P�ʕ����̘a���P���܂��B
�i����̘a��23�ɂȂ�悤�ȑ��̒P�ʕ����̘a�͂�����傫���Ȃ�j
�E(1)�̏ꍇ�́A���ʓ��̕����l���āA
�@�@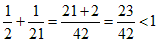
�̂悤��2�̒P�ʕ����̘a��1�������܂���B
�i����̘a��23�ɂȂ�悤�ȑ��̒P�ʕ����̘a�͂����菬�����Ȃ�j
�E(2)�̏ꍇ�i3�̐����̘a��23�̂Ƃ��j���ׂ������ׂ܂��B
a)2�{2�{19�@�@�@b)2�{3�{18�@�@�@c)2�{4�{17�@�@�@d)2�{5�{16�@�@�@e)2�{6�{15�@�@�@f)2�{7�{14
g)2�{8�{13�@�@�@h)2�{9�{12�@�@�@i)2�{10�{11�@�@�@j)3�{3�{17�@�@�@k)3�{4�{16�@�@�@l)3�{5�{15
m)3�{6�{14�@�@�@n)3�{7�{13�@�@�@o)3�{8�{12�@�@�@p)3�{9�{11�@�@�@q)3�{10�{10�@�@�@r)4�{4�{15
s)4�{5�{14�@�@�@t)4�{6�{13�@�@�@u)4�{7�{12�@�@�@v)4�{8�{11�@�@�@w)4�{9�{10�@�@�@x)5�{5�{13
y)5�{6�{12�@�@�@z)5�{7�{11�@�@�@aa)5�{8�{10�@�@�@ab)5�{9�{9�@�@�@ac)6�{6�{11�@�@�@ad)6�{7�{10
ae)6�{8�{9�@�@�@af)7�{7�{9�@�@�@ag)7�{8�{8
a)�̏ꍇ�́A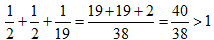 �̂悤��1���Ă��܂��܂��B
�̂悤��1���Ă��܂��܂��B
b)����ag)�̏ꍇ�́A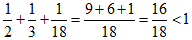 �̂悤��1�ɂƂǂ��܂���B
�̂悤��1�ɂƂǂ��܂���B
�i����̘a��23�ɂȂ�悤�ȑ��̒P�ʕ����̘a�͂����菬�����Ȃ�j
���c��̂́A(3)�̏ꍇ�i4�̐����̘a��23�̂Ƃ��j�ł��B
a)2�{2�{2�{17�@�@�@b)2�{2�{3�{16�@�@�@c)2�{2�{4�{15�@�@�@d)2�{2�{5�{14�@�@�@e)2�{2�{6�{13
f)2�{2�{7�{12�@�@�@g)2�{2�{8�{11�@�@�@h)2�{2�{9�{10�@�@�@i)2�{3�{3�{15�@�@�@j)2�{3�{4�{14
k)2�{3�{5�{13�@�@�@l)2�{3�{6�{12�@�@�@m)2�{3�{7�{11�@�@�@n)2�{3�{8�{10�@�@�@o)2�{3�{9�{9
p)2�{4�{4�{13�@�@�@q)2�{4�{5�{12�@�@�@r)2�{4�{6�{11
s)2�{4�{7�{10�@�@�@t)2�{4�{8�{9�@�@�@u)2�{5�{5�{11�@�@�@v)2�{5�{6�{10�@�@�@w)2�{5�{7�{9
x)2�{5�{8�{8�@�@�@y)2�{6�{6�{9�@�@�@z)2�{6�{7�{8�@�@�@aa)2�{7�{7�{7�@�@�@ab)3�{3�{3�{14
ac)3�{3�{4�{13�@�@�@ad)3�{3�{5�{12�@�@�@ae)3�{3�{6�{11�@�@�@af)3�{3�{7�{10�@�@�@ag)3�{3�{8�{9
ah)3�{4�{4�{12�@�@�@ai)3�{4�{5�{11�@�@�@aj)3�{4�{6�{10�@�@�@ak)3�{4�{7�{9�@�@�@al)3�{4�{8�{8
am)3�{5�{5�{10�@�@�@an)3�{5�{6�{9�@�@�@ao)3�{5�{7�{8�@�@�@ ap)3�{6�{6�{8�@�@�@ aq)3�{6�{7�{7
ar)4�{4�{4�{11�@�@�@as)4�{4�{5�{10�@�@�@at)4�{4�{6�{9�@�@�@au)4�{4�{7�{8�@�@�@av)4�{5�{5�{9
aw)4�{5�{6�{8�@�@�@ax)4�{5�{7�{7�@�@�@ay)4�{6�{6�{7�@�@�@az)5�{5�{5�{8�@�@�@ba)5�{5�{6�{7
bb)5�{6�{6�{6
a)����r)�܂ł́A
�@�@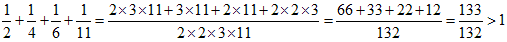
�ƂȂ�A1�ȏ�ł��B
ac)����bb)�܂ł́A
�@�@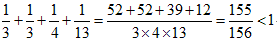
�ƂȂ�A1�ȉ��ł��B
s)����ab)�܂ł͈�ЂƂ��ׂ܂��B
�@�@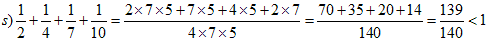
t)��s)�����������̂łP�ɂ͂Ȃ�܂���B
�@�@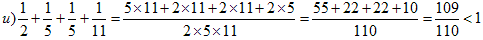
v)�Aw)�Ax)��u)��菬�����̂łP�ɂ͂Ȃ�܂���B
�@�@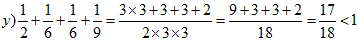
z)�Aaa)��y)��菬�����̂łP�ɂ͂Ȃ�܂���B
ab)�͖��炩�ɂP���傫���ł��B
�܂�A(3)�̏ꍇ�ɂ��K������̂�����܂���B
�i�P�j�ɂ��čl���܂��B
�藝�u�V�V�ȏ�̑傫�Ȑ����́A�K���ȕ��������݂��āA�����������̋t���i�P�ʕ����j�̘a��1�ɂ��邱�Ƃ��ł���v
�Ƃ������Ƃł����A���łV�V���������Ȑ����V�U�Ő������邱�Ƃ�������Ă��܂��B
������ƕςȊ����ł��B
�Q�S����V�T�܂ł̐����ɂ��Ē��ׂĂ݂�Ƃ��ׂđ�ӂ���������܂��B
����āA�Q�R�������ɂȂ�܂��B
�Q�S����V�T�܂ł̗�
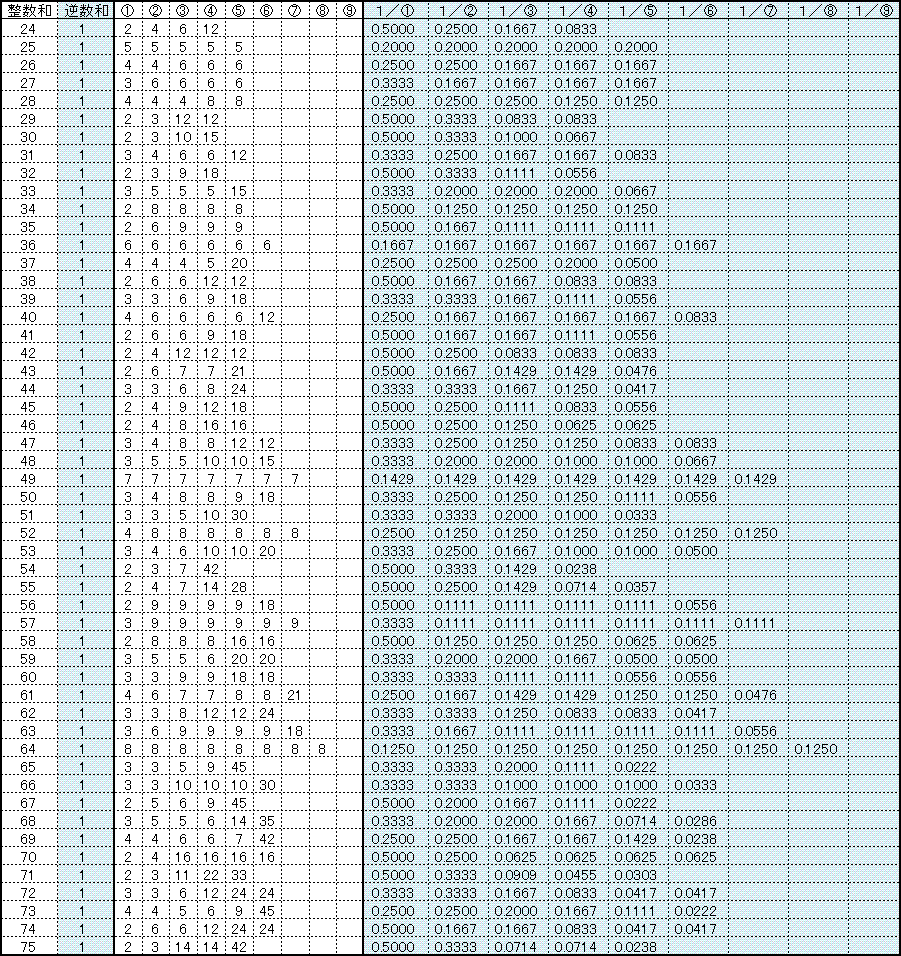
1997�N�̐R�w�@�������̖������肵�ďo�肵�܂��B
1�ӂ��U�����̐��l�ʑ̂`�|�a�b�c������A�ӂ`�a�C�`�b�C�c�a�C�c�b���P�F�Q�ɓ�������_�����ꂼ��d�C�e�C�o�C�p�Ƃ����B
�ʂd�e�p�o�Ő����钸�_�`���܂ޑ��̕����̑̐ς����߂�B
���Ȃ݂ɁA�d�e�C�o�p��ʂ�A�ʂd�o�p�e�Ɛ����Ȗʂ��`�c�ƌ����_�����ꂼ��f�C�q�Ƃ��܂��B
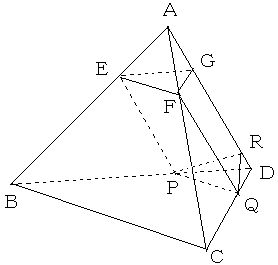
�܂��A��ʂɐ��l�ʑ̂`�|�a�b�c�̑̐ς��u�Ƃ��A
�ӂ`�a�C�`�b�C�c�a�C�c�b���P�F�i���|�P�j�ɓ�������_�����ꂼ��d�C�e�C�o�C�p�Ƃ����A
�ʂd�e�p�o�Ő����钸�_�`���܂ޑ��̕����̑̐ς��s�Ƃ����Ƃ��A�u�F�s�̔�����ŕ\���B
���F���̋L���Ɋւ��铊�e�̌f�ڂ́A2011�N4��25���ȍ~�Ƃ��܂��B
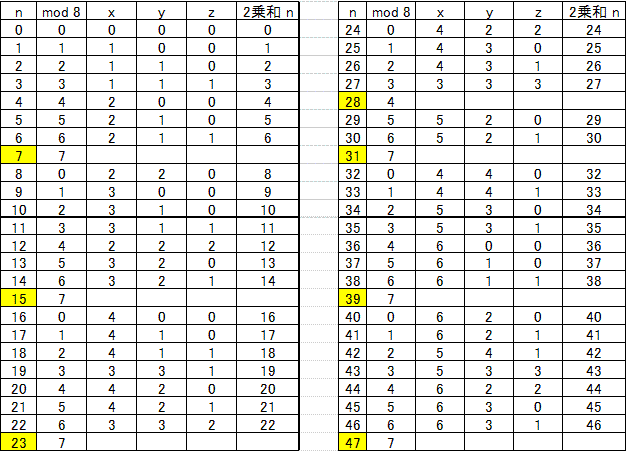
�i�P�j7,15,23,28,31,39,���
�@�@
�i���̑g�ݍ��킹������ꍇ������܂��j
�i�Q�j0,1,4
�����R����4�̔{�������Ƃɕ��ނ���ƁA�o4k�|3�C4k�|2�C4k�|1�C4k�p��4��ނ̃^�C�v�ɕ�����܂��B
���ꂼ��2�悷��ƁA
�@�@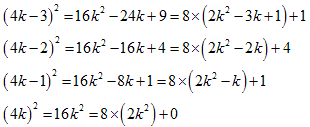
����Ď��R�������̕�����8�Ŋ������Ƃ��̗]��ŕ��ނ���Ǝ���3��ނɕ�����܂��B
�E�]��0�@�����@���R����4�̔{���̋����̂Ƃ��@�@�@�o4, 8, 12, 16, ��� �p���y�O�z�ŕ\�����Ƃɂ��܂�
�E�]��1�@�����@���R������̂Ƃ��@�@�@�@�@�@�@�@�o1, 3, 5, 7, 9, ��� �p���y�P�z�ŕ\�����Ƃɂ��܂�
�E�]��4�@�����@���R����4�̔{���łȂ������̂Ƃ��@�o2, 6, 10, 14, ��� �p���y�S�z�ŕ\�����Ƃɂ��܂�
�i�R�j�l�@
��8�Ŋ������Ƃ��̗]�肪7�ɂȂ�o7, 15, 23, 31, ����p�Ȃǂ́A3�̕������̘a�ŕ\�����Ƃ͂ł��܂���B���Ȃ��Ƃ�4���K�v�ł��B
�Ⴆ�A
�@�@�@�@�@ �y�S�z�{�y�P�z�{�y�P�z�{�y�P�z�̌`
�y�P�z�{�y�P�z�{�y�P�z�{�y�P�z�{�y�P�z�{�y�P�z�{�y�P�z�̌`
�@�@�@�@�@�y�P�z�{�y�S�z�{�y�P�z�{�y�P�z�̌`
�@�y�S�z�{�y�S�z�{�y�S�z�{�y�P�z�{�y�P�z�{�y�P�z�̌`
�@�@�@�@�@�y�P�z�{�y�P�z�{�y�S�z�{�y�P�z�̌`
�@�@�@�y�O�z�{�y�S�z�{�y�P�z�{�y�P�z�{�y�P�z�̌`
�@�@�@�@�@�y�P�z�{�y�S�z�{�y�P�z�{�y�P�z�̌`
�@�@�@�@�@�y�S�z�{�y�P�z�{�y�P�z�{�y�P�z�̌`������
�y�O�z�A�y�P�z�A�y�S�z�̃O���[�v����3�����ǂ��g�ݍ��킹�Ă��a�́o7, 15, 23, 31, ����p�ɂȂ�܂���B
��28�́A8�Ŋ������Ƃ��̗]�肪4�ł��B
�����ŁA
�@�y�S�z�{�y�O�z�{�y�O�z�̌`�̏ꍇ�A
�A�y�S�z�{�y�S�z�{�y�S�z�̌`�̏ꍇ���l�����܂��B
�y�O�z�F�o4, 8, 12, 16, ����p�A�y�S�z�F�o2, 6, 10, 14, ����p�̐������ꂼ�ꕽ������ƁA
�o16, 64, 144, ����p�A�@ �@�o4, 36, 100, ����p�ł��B
�������A
�A �S�z�{�y�O�z�{�y�O�z�A
�A�y�S�z�{�y�S�z�{�y�S�z�̂悤�ɑg�ݍ��킹�Ęa��28�ɂ͂��邱�Ƃ͂ł��܂���B
������3�̕������̘a�ƂȂ�ɂ́A8�Ŋ������Ƃ��̗]��ŕ��ނ��āA
�E�]��0�̂Ƃ��A�@�y�O�z�{�y�O�z�{�y�O�z�A�y�S�z�{�y�S�z�{�y�O�z
�E�]��1�̂Ƃ��A�@�y�P�z�{�y�O�z�{�y�O�z�A�y�P�z�{�y�S�z�{�y�S�z
�E�]��2�̂Ƃ��A�@�y�Q�z�{�y�O�z�{�y�O�z�A�y�Q�z�{�y�S�z�{�y�S�z�A�y�P�z�{�y�P�z�{�y�O�z
�E�]��3�̂Ƃ��A�@�y�P�z�{�y�P�z�{�y�P�z
�E�]��4�̂Ƃ��A�@�y�S�z�{�y�O�z�{�y�O�z�A�y�S�z�{�y�S�z�{�y�S�z
�E�]��5�̂Ƃ��A�@�y�P�z�{�y�S�z�{�y�O�z
�E�]��6�̂Ƃ��A�@�y�P�z�{�y�P�z�{�y�S�z
�̌`�̐���I�Ԃ̂��K�v�����ł��B
���]�肪3�̂Ƃ��͏ꍇ�������Ă��܂��B�o3,11,19,27,�������p
�Ex�Ay�Az�̒���1������Ƃ��A���̊3�ɂ���A ��������̂ŁA���̐��ɂȂ�܂��B
�Ex�Ay�Az�̒��ɓ������1�g����Ƃ��A1�����̊�ɁA����1����O�̊�ɂ���ƁA
�ƂȂ�̂ŁA���̐��ɂȂ�܂��B
�Ex�Ay�Az�̒���2�̊�����Ԃ�p�Ⴄ�Ƃ��A�傫���������̊�ɁA������������O�̊�ɂ���ƁA
�ƂȂ�̂ŁAp�{1���̐��ɂȂ�܂��B
�E�A�������̕����̍��ׂ܂��B�ik�Ԗڂ�k�{1�Ԗځj
�ƂȂ�܂��B
����́A ��8�~1��8�������A ��8�~2��16�������A ��8�~3��24�������܂��B
2k�|1��2k�{1�ɑ��₷�ƁA8k�������܂��B
2k�|1��2k�|3�Ɍ��炷�ƁA8(k�|1)�������܂��B
�E�ȏ�̂��Ƃ����g�ݍ��킹��ƁA�Ⴆ�A
�@�@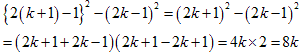
�ƂȂ�܂��B
������Ƃ݂Ă��܂��A8�Ŋ�����3�]�鐔�́A3�̊�̕����a�ŕ\�����Ƃ��ł���Ǝv���܂��B
�藝�u�V�V�ȏ�̑傫�Ȑ����́A�K���ȕ��������݂��āA
�����������̋t���i�P�ʕ����j�̘a��1�ɂ��邱�Ƃ��ł���B�v
���Ƃ��A�������Ă��邻���ł����A���ׂĂ݂��
�@�@�@76 = 2 + 4 + 10 + 20 + 20 + 20
�@�@�@77 = 3 + 4 + 5 + 5 + 60
�@�@�@78 = 2 + 6 + 8 + 10 + 12 + 40
�ƂȂ�A��ӂ��\�ƂȂ�܂����B����ŁA
�@(1) ��ӂ̂��Ƃ��A���藧���Ȃ�����������Ă��������B
�@(2) �V�V�ȉ��ł́A���̂悤�ȕ��������݂��Ȃ���������Ƃ������Ƃł����A�Q�R�͑�ӂ̂��Ƃ��A�s�\�ł��邱�Ƃ������Ă��������B
���̍�����R�ɂ��Ẳ��A�Ē����L��������܂����B
�e��R��S�ĂP�Ƃ�����ʂȏꍇ�ł������A
����͒�R�̒l�����R�ɂƂ����ꍇ�̕s�����ɂ��čl���Ă݂܂����B
�Q�̒�R�l�ɂ��ẮA����ƕ���ŁA���ꂼ��̒l�́A
�@�@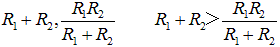
����������B
�R�̒�R�l�ɂ��ẮA����ƕ��g�ݍ��킳��āA���ꂼ��̒l�́A
�@�@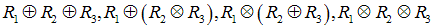
�������v�Z���āA��r����ƎO������
�@�@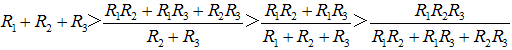
����ƕ���̐�������A��Εs������������܂����B
�@�@