NO.1921 この角何度 2011.2.21. 水の流れ
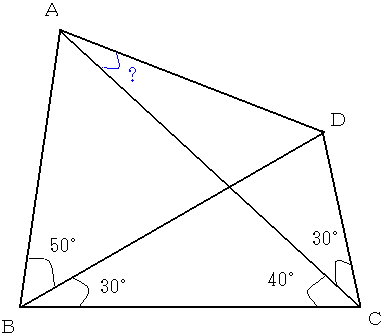
四角形ABCDにおいて、∠ABD=50°,∠DBC=∠ACD=30°,
∠ACB=40°のとき、∠CADは何度か。
注:この記事に関する投稿の掲載は、2011年3月14日以降とします。
ColloquiumNO.266
|
四角形ABCDにおいて、∠ABD=50°,∠DBC=∠ACD=30°,
∠ACB=40°のとき、∠CADは何度か。

注:この記事に関する投稿の掲載は、2011年3月14日以降とします。
● 4|x|+3|y|=12 のグラフは、
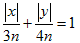 と変形すると、切片が (3n,0),(0,4n),(-3n,0),(0,-4n) であるような菱形です。
と変形すると、切片が (3n,0),(0,4n),(-3n,0),(0,-4n) であるような菱形です。
調べる領域は菱形の内部です。
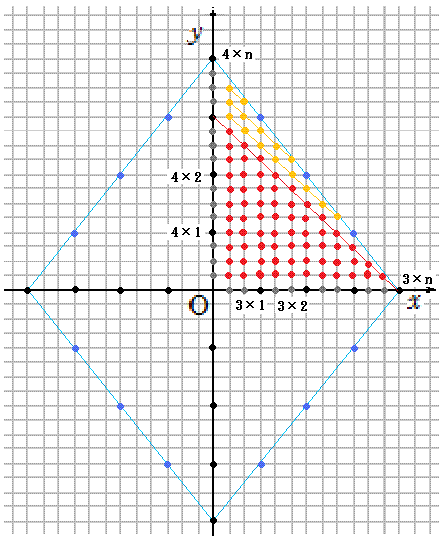
(1)x,yがともに自然数であるときは、第1象限です。
1)図の赤色の部分(傾き-1の赤線以下の部分)
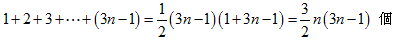
2)図の黄色の部分(傾き-1の線で分類して数える。nが2,3,・・・,nと変わると、3ずつ増える)
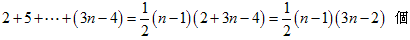
3)図の青色の部分(直線上のところ)
n-1 個
以上から、
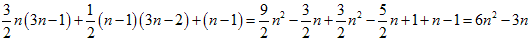
(2)x軸上の点は、3n×2+1個、y軸上の点は、4n×2+1個、原点を重ねて数えているので、計14n+1個
(3)(1)の答えを4倍して(2)の答えを足すと、
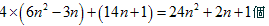
●後半の準備
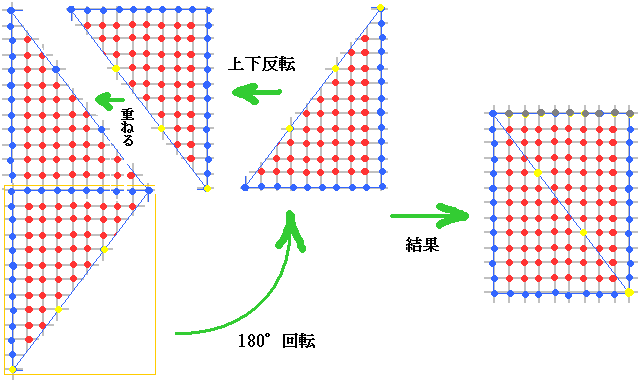
上の図のように元の図形を等積で長方形に変形します。
黄色の点は、数えるべき点が重なってしまう点です。(3個・・・n個)
灰色の点は、数えなくてもよい点です。(9個・・・3n個)
元の三角形では(1+3+5)+(9+11+13)+(17+19+21)+25=124個の点があります。
長方形にすると、10×13+3-9=124
(4)境界線上の点は、
軸上の点 4
軸以外の点 4×(n-1)
合計 4n
(5)面積は菱形なので、対角線の長さの積の半分です。つまり 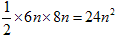
(6)次の図を参考に考えます。
全ての抵抗を1として、抵抗の個数とその時、取りうる抵抗値は、
2個のとき、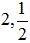
3個のとき、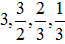
4個のとき、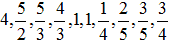
5個のとき、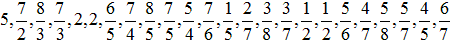
となると思います。抵抗値の逆数が、同じ個数で存在します。
図の回路を代数的に、数式で1対1に表現できます。
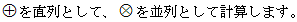
並列が優先で計算され、かっこが優先されるのは通常の計算と同じです。
上の図の計算式は、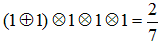
対して、逆数の場合は、 を交換してみると
を交換してみると
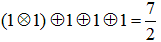 が得られ、数式からすぐに図が作れます。
が得られ、数式からすぐに図が作れます。
「すべての抵抗値を1として、抵抗の個数N個のとき、Aの値を持つ抵抗の回路が存在すれば、
その逆数の値1/Aをもつ、抵抗個数のN個の回路が存在する。」
抵抗の数kについての帰納法で、簡単に証明することができます。
k=2のとき
直列のとき 抵抗値は2、並列のときは、1/2となり正しい。
k=n 以下の数について成り立つとして、
k=n+1のとき、回路の図を式に表したとき、適当に二つに分けることができる。

よって、帰納法の仮定より、全ての個数について命題が成り立つ。
問1
明らかに凸領域、すなわち、その中の任意の2点を結ぶ線分を完全に含んでいる領域に
制限して議論すれば十分である。
問1.の証明のために、次の二つの補助定理を証明する。
補助定理1
下底と上底と高さの等しい全ての台形の中で、その脚の長さの和が最小なのは、等脚台形である。
証明
ABCDを下底BC、上底AD,脚AB、CDの任意の台形とする。
ADの垂直二等分線に関するBの鏡像をB’とし、CB’の中点をC0とする。
CBの延長線上にBB0=CC0となりように点B0をとり、
等脚台形AB0C0Dを作る。
等脚台形の下底と上底と高さは与えられた台形のそれと等しいので、その面積も等しい(fig.1)
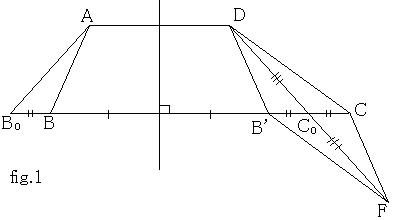
ここで、DC0をその長さだけ延長し、その終点をFとすると、平行四辺形DCFB’が得られる。(fig.1)
その対角線DFの長さは、辺DCとCFの長さの和よりも短い。
DF<DC+CF
ところが、DF=2・DC0=DC0+AB0であり、
CF=DB’=ABだから、
AB0+DC0<AB+DC
となっている。このことから等脚台形のときに、脚の長さの和が最小になることがわかる。
(証明終わり)
補助定理2
円長最小の平面領域には、全ての方向に対して対称軸が存在する。
証明
ここで、与えられた面積Jを持ち、周長が最小の領域を F とし、その円長を u とおく。
領域 F に任意の直線 g を引き、gに垂直な直線で、 F を多くの
十分に細い台形ABCDに分割して、弧状の脚AB、CDを直線分で近似して考える。
分割線・・・、AD、BC、・・・と g との交点から、その分割線上の g の両側に、
弦・・・、AD、BC、・・・の半分の距離の点・・・、A’、D’、B’、C’、・・・をとり、
台形・・・、A’B’C’D’、・・・を考える。
この新しい台形A’B’C’D’は、等脚台形であり、その下底、上底、高さは、
台形ABCDのそれと等しいから、その面積も等しい。
このとき、補助定理1より
A’B’+C’D’≦AB+CD ・・・式1
であり、台形ABCDも等脚台形のときだけ、等号が成立する。
この方法により、 F から対称軸 g をもつ 新たな領域 F’ が得られる。
その面積は、 F と等しいから、その周長も等しくなる。
なぜなら、その値は、u より小さくなれないからである。
つまり、式.1の等号はどこでも成り立つので、全ての台形ABCDは等脚台形になり、
BCの垂直二等分線が F の対称軸になっている。
したがって、周長最小の平面領域 F には、全ての方向に対して対称軸が存在する。(証明終わり)
以上二つの補助定理を利用して、問1の命題が証明できる。
証明
ⅠとⅡを直行する F の対称軸とし、Mをその交点とする。
F の任意の点PのⅠに関する鏡像をP1、
Ⅱに関するP1の鏡像をP’とする。このとき、PMP’は直線であり、
MP’=MP
が成り立つ。このような点Mを領域 F の中心とよぶ。
さらに、 F は1つしか中心を持たない。
仮に、第2の中心Nがあったとする。まず、PMをその長さだけ延長すると、
P’に至る。次にP’Nをその長さだけ延長すると、
F の新たな点P''に至る。さらにP''Mをその長さだけ延長すると、
F の点P'''に至り、P'''Nをその長さだけ延長すると、再び
F の別な点に至る・・・・。
この操作を絵に描いてみるとわかるように、これを繰り返していくと、
F が描かれている紙の範囲を超えて
、どんどん遠くまでいってしまう。
もちろん、これはおかしい。したがって、 F は唯一の中心Mを持つ。
さらにMは、 F のどの対称軸にも含まれていることがわかる、
実際、Mが、 F の対称軸hに含まれないならば、hに関するMの鏡像mと
領域内の任意の点Pの鏡像pが作図できる。
pMをその長さだけ延長して領域内にp'をとり、hに関するp'の鏡像p''を作図する。
ここで、p''は、 F の点であり、Pmp''は直線で、mp''=mPだから、
F が第2の中心mを持つことになってしまう。しかし、これは不可能である。
そこで、点Fを F の境界上の固定点として、Qを F の境界上の任意の点とする。
FQの垂直二等分線は、 F の対称軸の1つだから、Mを通る。したがって、
MQ=MF
つまり、 F の境界上のすべての点はMから等距離にある。
よって、その領域 F は円である。
故に、面積の等しいすべての平面領域の中で、周長が最小になるものは円である。(証明終わり)
問2
問1の結果を利用して、問2の命題が証明できる。
証明
円ではない任意の領域 F の周長 f が円領域 K の周長 k に等しいとする。
また、 F の面積をF、K の面積をKとする。
このとき、F≧Kとすると、 K と同心の円領域 K' で、
その面積がK'=Fであるものを考え、その周長を k' とする。
K' は、 K を含んでいるから、
k'≧k ・・・式.2
である。ところが、 F と K の面積が等しいから、問1の結果より、
k'<fとなり、
k'<k ・・・式.3
を得る。しかし、式.2と式.3は互いに矛盾するから、F≧Kという仮定が間違っていることになる。
したがって、F<Kとなる。
故に、周長の等しいすべての平面領域の中で、面積が最大になるものは円である。(証明終わり)
1.当然と思える問題・その1
当然と思える問題・その1でもそうなのですが、
周長や面積が最大/最小になったり、正なんとか角形になったりするのは、
状況の対称性が本質だと思えます。
例えば、円に内接する三角形の面積最大が、正三角形になるのは、
図-1のように三角形の底辺aを水平に固定して考えれば、
頂点Aを円に沿って動かしたとき、左右の対称軸s上にある点Cで、
面積が極値をとる事はすぐわかります。
何故ならCにおいては、左右からの接近(矢印)による面積の増分が左右対称なので、
増分をdSとすれば、dS=-dSが必要で、dS=0となるからです。CでSが極大値を取り、
しかも唯一の極大値で最大なのは、図から明らかです。これらも円の等方性を利用すれば、
dS=-dSみたいな論拠で、じつは定性的に何とかなりそうです。
結論として、底辺aを固定して考えれば、b=cの二等辺三角形のとき、面積最大となります。
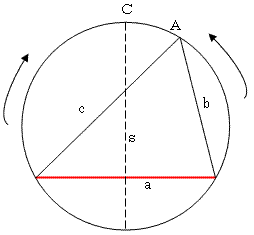 後は円の等方性を利用し、bがaに重なるように回転させれば、a=cです。
従ってb=c=aのときの正三角形で、面積最大となるのがわかります。本質は、
後は円の等方性を利用し、bがaに重なるように回転させれば、a=cです。
従ってb=c=aのときの正三角形で、面積最大となるのがわかります。本質は、
・円の等方性という、対称性.
だと思います。
では、「当然と思える問題・その2.問1.」です。
これも円の等方性を利用すれば何とかなる!、というのが自分の印象です。でも出来ませんでした。
それで腕力に訴え、計算過程を事後に見渡して定性的説明ができないものかと試みましたが・・・。
2.腕力で計算
領域を囲む曲線をCとします。問題の条件は、面積不変ですから、面積Aを定数とします。
面積Aは、C上の線積分で、次のように表せます。
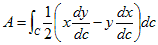 (1)
(1)
ここで曲線Cのパラメータcは、Cの弧長だとします(便利なので)。
Aは定数なので、(1)の(x,y)に関する変分は0です。まずAの(x,y)に関する変分を取ります。
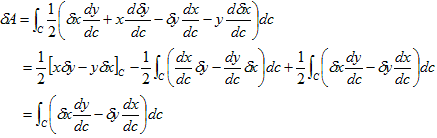 (2)
(2)
(2)の2段目から3段目の移行では、
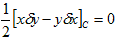 (3)
(3)
を使っています。(3)は、閉曲線Cの起終点での値の差を表し、Cの起終点はCが閉なので同じであり、当然差も0、という話です。
次に変分(δx,δy) について考えます。(δx,δy)は曲線の変分なので、
δx,δyの内の1個は、自由に選べます。例えば通常の変分では、y=f(x)と考えるので、
δx=0かつδy任意です。ここでは、
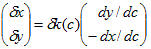 (4)
(4)
と必ず変分を、曲線Cの外法線方向へ向くように制限します。制限できて便利だからです。δk(c)が、実質的な曲線Cの変分です。(4)を使うと(2)は、
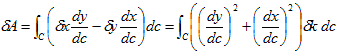
となりますが、cが曲線Cの弧長パラメータなので、
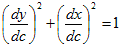 (5)
(5)
が成り立ちます(便利だ!)。よって、
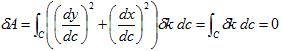 (6)
(6)
です。これはある意味、面積不変の条件から導かれる、当然の結果です。
次に曲線Cの長さは、次式で表されます。
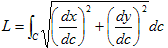 (7)
(7)
これの(x,y)に関する変分をとると、次式が得られます。
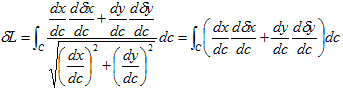
中辺から最右辺への移行に関しては、(5)を使ってます。部分積分し、(3)に関するのと同じ注意のもとで、
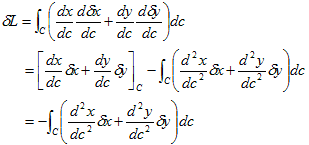
です。さらに(4)を使い、
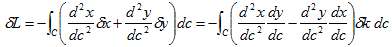 (8)
(8)
となります。
準備OKなので、次の変分問題を考えます。
・(1)不変という制約条件のもとで、(7)を最小化する。 (9)
(9)の必要条件は、次で与えられますが証明しません(出来ません・・・)。
でもラグランジュの未定乗数法です。
[定理]
(1)不変の制約条件のもとで、(7)を最小化する必要条件は、ある定数λが存在し、
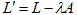 (10)
(10)
の変分が0になる事。
とにかく[定理]を使います。λは定数で、LとAの変分は既に求めてありますから、(10)より
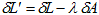
となり、(6)と(8)を代入すれば、
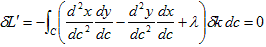
です。変分δkは任意なので、
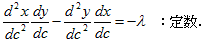 (11)
(11)
が得られます。ここでcがCの弧長パラメータである事を思い出すと、cの関数hがあり、
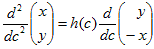 (12)
(12)
となります。cに関する2階微分は常に、Cの接線ベクトルに直行するからです。
これはcの定義から直接導けます(便利だ!)。(12)を(11)に代入すれば、
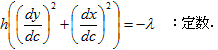
です。これに(5)を考慮すると、
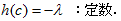 (13)
(13)
という結果になります。この結果には、少々びっくりしました。ポイントは(12)です。
cは曲線Cの弧長パラッメータなので、いまC上の質点mの運動を考えると、(12)の左辺は、
質量mも速度vも全て、1に規格化された状態での質点加速度と考えられます。つまりm=1かつ、
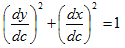
です。(12)は、曲線の局所的な曲率半径に載った円運動の、運動方程式と考えられます。
(12)の左辺は、曲率中心への向心加速度です。一般にはその大きさh(c)が、cの場所ごとに変わるので、
ぐにゃぐにゃな曲線という訳です。
いまそのh(c)が(13)より、曲線の場所cによらず一定です。
このような運動は、円運動しかありません。従ってCは円です。
3.定性的説明求む
2.で、状況の対称性が関係した部分はどこでしょうか?。(11)の左辺がh(c)になるのは、一般的話なので、
右辺が定数になるところに、対称性が関係します。-λの項は、面積の変分、
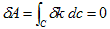 (14)
(14)
から出てきました。(14)中辺を見れば明らかなように、面積の変分は特定の点にも方向にも依存しません。
つまり、
(a)面積の変分は、等方かつ一様性を持つ.
です。これは、面積という量が純粋に図形の内部性質で、図形の形だけで決まるという、当然と言えば当然の結果です。もう一つは、[定理]が使えるためには、面積不変の条件も必要です。それは(14)の=0で表されます。
(b)面積不変の条件も必要.
(a),(b)を合わせると、(13)も考慮して、
・面積不変なら、周の最短曲線の曲率変化は、その場所での面積変化に比例する.
・面積は等方量であるから、そのような曲線は、円しかない.
と言えそうなのですが、1.のようなステップが踏めません。どなたか、幾何学音痴(計算屋)にアドバイスをお願いします・・・。
この問題は任意の有理数の値の抵抗が作れるかを示せば十分だと思います。
「抵抗の個数が、1,2,3,4,5個のとき、それぞれ本質的に異なるものは、1、2、4、10、24通り」あることは調べていませんが、抵抗の個数に制限がないとして任意の抵抗を作れることを見ます。
抵抗は直列につなげば和がその抵抗値になります。
抵抗は並列につなげば逆数の和の逆数が抵抗になります。
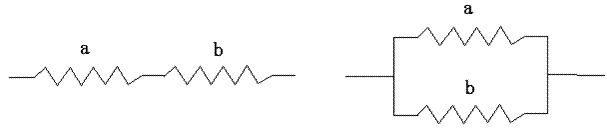
左の図の合成抵抗は、 a+bです。
右の図の合成抵抗は、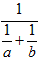 です。
です。
有理数 m/n の抵抗を作ります。
m>nの場合は割り算をして整数部分kと真分数 l/n の部分に分けます。
次に真分数の部分を単位分数 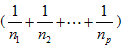 に分けます。
に分けます。
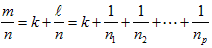
これは次のように抵抗をつなげれば実現できます。
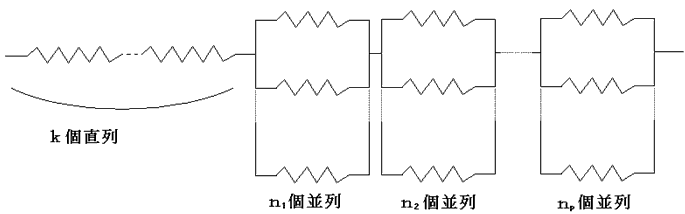
●問2からやります。
先ず、周の長さを一定にしたときn角形のうち面積の最大は正n角形であることをいいます。
次にnが増加すると面積が大きくなることをみます。
するとn→∞の極限として円になります。
問1は問2から簡単に納得できます。
●周の長さが一定の図形の面積
(1)三角形の場合
△ABCの辺ABを固定し、頂点A、Bを焦点とし、AC+BC=一定となるような楕円をかきます。
図のように点C'をとれば、AB+BC+CA=AB+BC'+C'A、△ABC<△ABC'は明らかです。
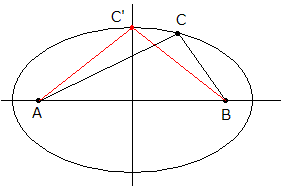
つまり、底辺を固定すれば、周の長さが一定の場合、二等辺三角形のとき面積が最大になります。
固定する辺を変えることを繰り返せば、周の長さが一定の場合、正三角形のとき面積が最大と考えられます。
(2)四角形の場合
□ABCDに対角線ACを引き、△BCAと△DACに分けます。
それぞれを(1)のようにして辺の長さの和が変わらないようにそれぞれ△B'CAと△D'ACに変形します。
(□D'AB'Cはタコ形です)
次に、□AB'CD'に対角線B'D'を引き、△AB'D'と△CD'B'に分けます。
同様にそれぞれ△A'B'D'と△C'D'B'に変形します。
(□D'AB'Cは菱形で、各辺の長さは等しくなります)
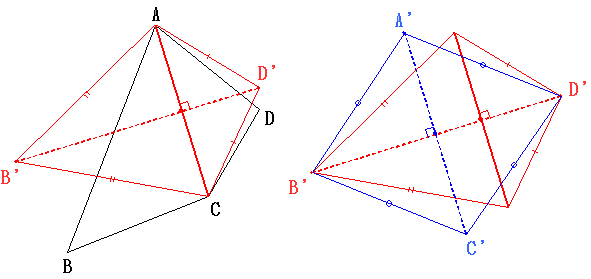
菱形は正方形(正四角形)のとき面積が最大になります。
(2)’三辺の等しい四角形の場合(準備)
※ 参照
これより3辺が等しい場合は等脚台形の場合が面積最大となります。(等脚台形は線対称の図形です)
(3)五角形の場合
五角形に対角線を引き2つの図形に分け三角形の方を①のようにして2辺の長さの和を変えずに二等辺三角形に直します。
この操作を繰り返していくと(最大の辺や最小の辺を考えながら)すべての辺の長さが等しくなります。
次ぎに②’のように四角形の方を等脚台形に直します。
すると線対称の各辺が等しい五角形にいなります。
この操作を繰り返していくと正五角形になります。
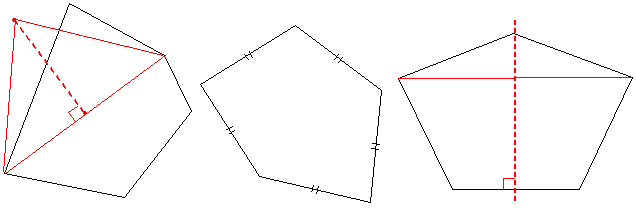
(4)n角形の場合
(1)、(2)’の操作を繰り返せば、正n角形になることがわかります。
(頂点を1つおきに結んで二等辺三角形をつくり、2つおきに結んで等脚台形をつくります)
以上から、n角形について、周の長さが一定なら正n角形のとき面積が最大と考えられます。
●次に正n角形を比較したとき何角形の面積が大きいか考えます。
○正n角形は円に内接します。(半径をrとします)
正n角形の周の長さを とします。隣り合う頂点と中心を結んで二等辺三角形を考えると等しい2辺の長さがrなので、余弦定理より
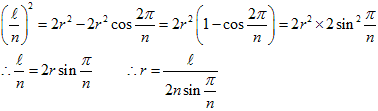
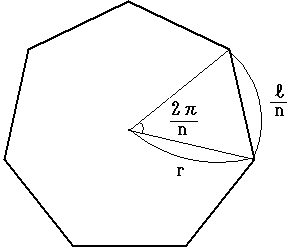
だから、正n角形の面積Sは
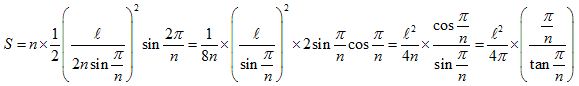
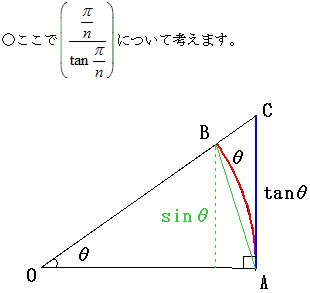
図のような△OABと半径1の扇形OABと直角三角形OACの面積を比較して、角θが鋭角のとき、
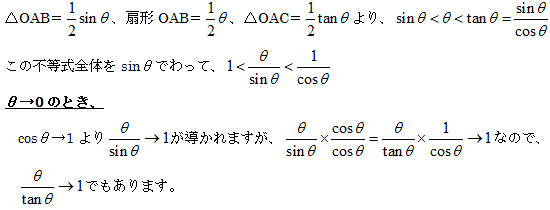
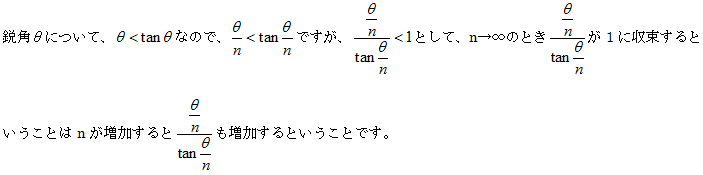
(上の図で中心角θが小さくなるほど弧の長さθと縦線のtanθの長さがどんどん差がなくなります)
以上から正n角形は、周の長さが一定のときnが大きいほど面積が大きくなります。
○n→∞の極限として円が考えられます。
●次に問1を考えます。
上のことから「周の長さが等しい図形で面積が最大となるのは円」です。
だから円Cを周の長さが変わらないように変形して図形DとするとDの面積はCより小さくなります。
次にDをCの面積と同じになるまで拡大した図形をD'とするとD'の周の長さは円Cより長くなります。
D'は円以外のすべての図形でかまわないので説明できたことになります。
●三辺の等しい四角形の場合を考えます。
図は、凹四角形、1つの内角が180°の四角形(三角形)、凸四角形、等脚台形の場合を示しています。
凹四角形は図のように辺の長さを変えずに凸四角形に変形できます。
凹四角形より凸四角形の方が大きいのは明らかです。
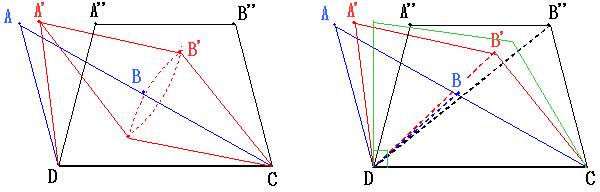
□ABCD(三角形)、□A'B'CDの面積を考えます。
右の図のように対角線で2つに分けて考えます。
それぞれAB(A'B')とBC(B'C')を底辺としDからの垂線の長さを高さとします。
底辺の長さは同じですが、高さはともに□A'B'CDの方が大きくなります。
よって、□ABCD<□A'B'CDとなります。
この考えは∠角A'が90°になるまで通用します。
しかし、∠A'が鈍角になると、△A'B'Dは直角のときより小さくなります。(高さが小さくなります)
●さて、□ABCDが等脚台形になる前後を調べます。
長さや角を図のようにおきます。
(後で用いるときのことを考えると2a<b<3aとしてよいと思います)
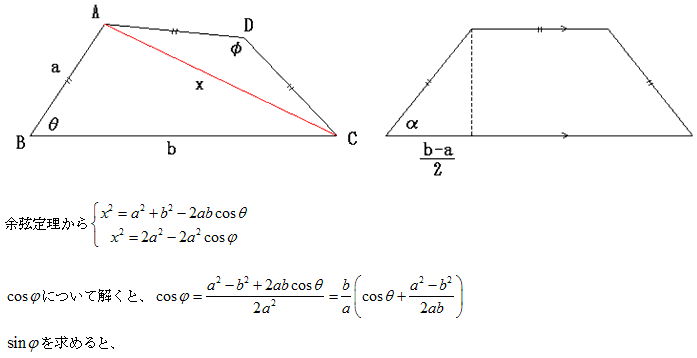

さてここであらかじめ等脚台形のときの面積 を求めておきます。
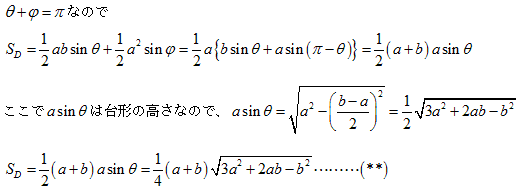
等脚台形のときの面積 が最大であることをいいたいので、(**)から(*)をひいて調べます。
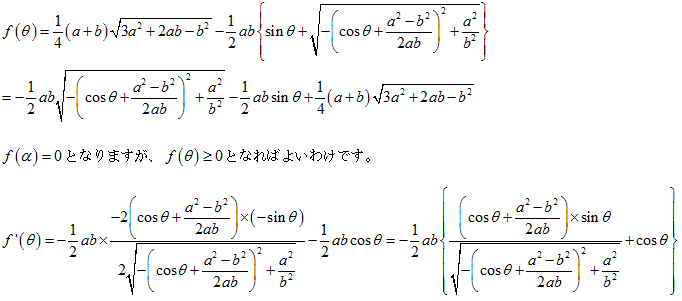
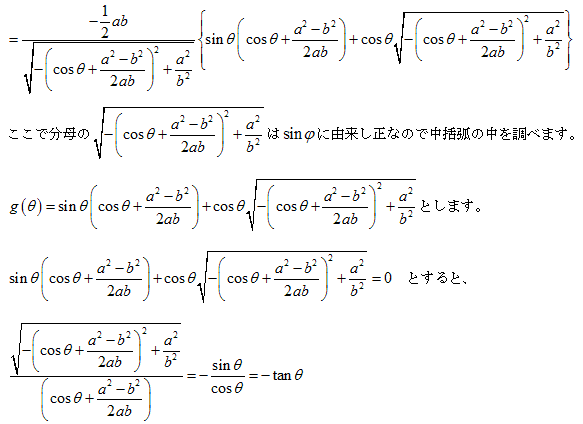
両辺を2乗すると、
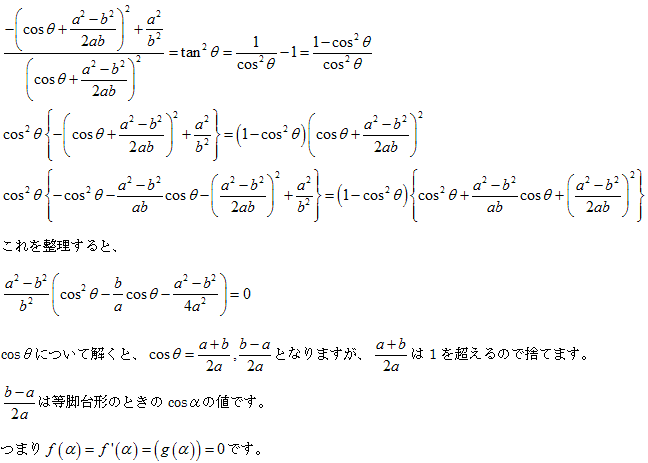
g(θ)について調べます。
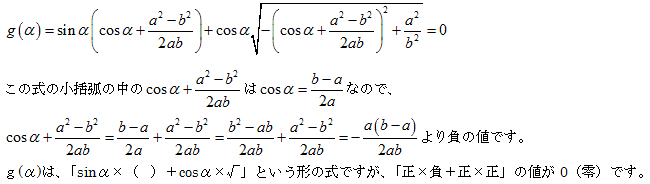
αより小さい角を α- 、大きい角を α+ で表します。
値の変化を「符号(絶対値の変化)」で表すことにします。
例えば、3→5は「正(大)」、-3→-2は「負(小)」、-3→-4は「負(大)」とします。
だから、
cosα→cos α- は「正(大)」、cosα→cos α+は「正(小)」、
sinα→sin α- は「正(小)」、sinα→sin α+は「正(大)」、
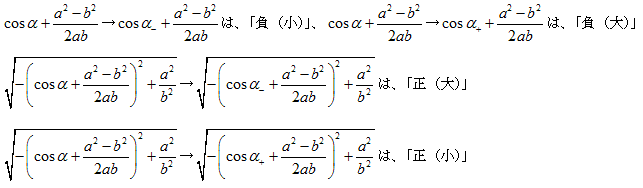
となります。

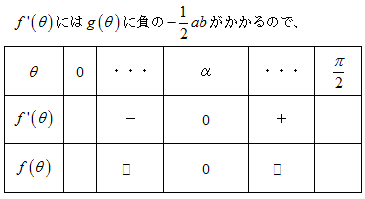
となり等脚台形ののとき面積が最大となります。
直列に並んでるものを並列に、またその逆にすれば…1:1対応する…
直列のもの=k
並列のもの=n-k
が並列に並んでるとき…
この場合…k と 1/(n-k) の抵抗なので…
1/{1/k+(n-k)}=k/{k(n-k)+1}
が合成抵抗値…
直列のもの=n-k
並列のもの=k
が直列に並んでるとき…この場合…n-k と 1/k の抵抗なので…
(n-k)+1/k=(k(n-k)+1)/k
と、丁度、逆数関係になっているのがわかる ^^
もっと複雑なときでも...全体で考えれば言えてると思うのですが...^^;?
f(1):1=1/1…1種類
f(2):2,1/2…2種類
f(3):3=1+2=3…2+2=4
f(4):4=1+1+2=1+3=2+2=4…2+4+2*2/2+2=10
f(5):5=1+1+1+2=1+1+3=1+4=1+2+2=2+3=5…2+4+10+2*2/2+2*4/2+2=24
並べる順番を考慮しなければこうなりますね…
f(n) の一般式って出せるんだろうか…?
数の分割式が出せれば使えそう…^^;?
電気抵抗の値をすべて1オームとして、つなげると、
抵抗の個数が、1,2,3,4,5個のとき、それぞれ本質的に異なるものは、
1、2、4、10、24通りとなります。
その抵抗値をみると、必ず逆数の抵抗値が存在することがわかります。
例えば、次の図の、5つの抵抗はすべて1オームとします。そのとき
全ての合成抵抗を、求めると 2/7 であることが分かります。
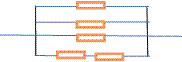
さて、逆に、5つの抵抗はすべて1オームで作る回路で合成抵抗の値が逆数の 7/2 の値を
持つ5つの抵抗でつくる回路が存在する。
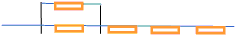
「一般に、合成抵抗値の逆数の値を持つものが、必ず存在することをしめしてください。」
