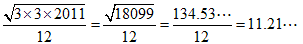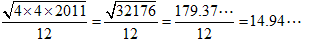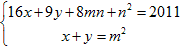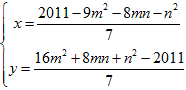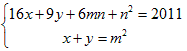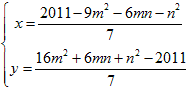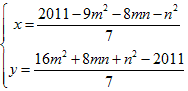ColloquiumNO.265
|
ｎを正の整数とする。座標平面上の点（ｘ，ｙ）が不等式４｜ｘ｜＋３｜ｙ｜≦１２ｎを満たす領域について、
次の問に答えよ。
なお、ｘ，ｙがともに整数である点（ｘ，ｙ）を格子点という。
また、｜ｘ｜は絶対値ｘを表す記号です。
（１）最初に、ｘ，ｙがともに自然数であるときの格子点の数をｎで表せ。
（２）領域にあって、両座標軸上の格子点の数をｎで表せ。
（３）領域にあるすべて格子点の数をｎで表せ。
さらに、別な解法として
（４）境界線上の格子点の数をｎで表せ。
（５）領域の面積を求めよ。
（６）（４），（５）を利用して、領域にあるすべて格子点の数をｎで表せ。
注：この記事に関する投稿の掲載は、2011年２月21日以降とします。
非常にばかばかしいことを考えたら、実際にそういう解があったという（苦笑）
一辺３の正方形を1296枚、一辺４の正方形を715枚、合計2011枚を用います。
一辺３の正方形を36枚＊36枚（1296枚）並べると、一辺の長さが108の正方形ができます。
一辺４の正方形を11枚＊27枚（297枚）並べると、一辺の長さが44と108の長方形ができます。
一辺４の正方形を11枚＊11枚（121枚）並べると、一辺の長さが44の正方形ができます。
これを組み合わせると一辺が152の正方形になります。
●3と4の最小公倍数が12なので、12を1辺とする正方形を1単位とします。
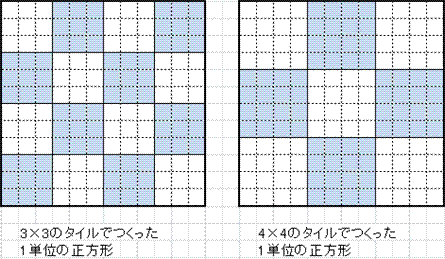
●その１
単位の正方形を縦横m×m単位個並べ、その外側2辺に 3×3のタイルをn個 の幅で埋めて正方形にします。
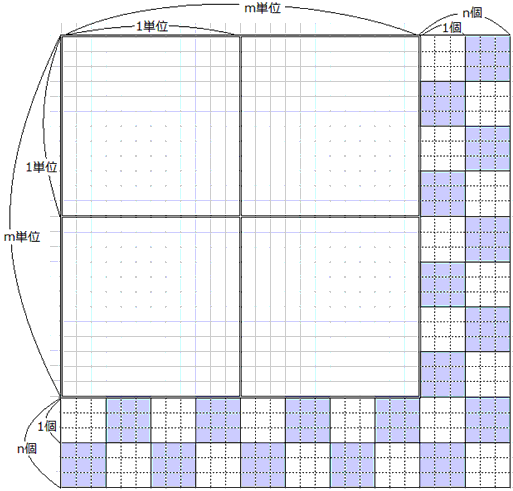
このとき、2011個すべてが3×3のタイルとすると、
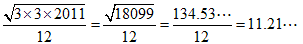
2011個すべてが4×4のタイルとすると、
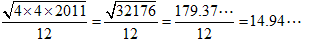
なので、11≦m≦14です。
またnは4になると単位の大きさになるので、0≦n≦3です。
単位の正方形として、3×3のものをx単位個、4×4のものをy単位個使い、
外側の2辺に3×3のものを 2×(4m)×n＋ｎ2 個使ったとすると
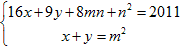
x、y をm、n で表すと、
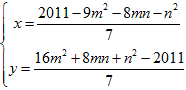
よって、
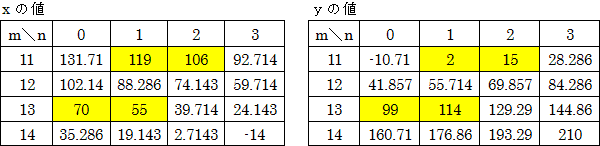
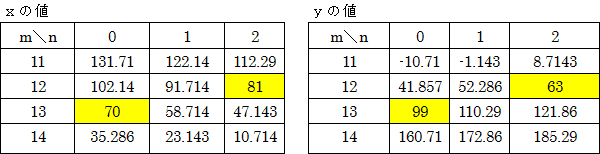
（x、yは同じ位置にあるものが対応します。黄色はともに整数になるところです。）
これから1辺の長さMは次のようになります。
●その２
単位の正方形を縦横m×m単位個並べ、その外側2辺に4×4のタイルをn個の幅で埋めて正方形にします。
mはその１と同様、11≦m≦14です。
またnは3になると単位の大きさになるので、0≦n≦3です。
単位の正方形で、3×3のものをx単位個、4×4のものをy単位個使い、
外側の2辺に3×3のものを 個使ったとすると
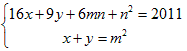
x、y をm、nで表すと、
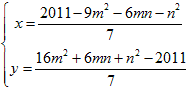
よって、
これから1辺の長さMは次のようになります。
n＝0のときは、その１の解と同じになります。
●おまけ
その１の連立方程式
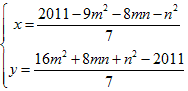
の解を探すとき、分子が7で割り切れるかどうかが要点です。
だからその数を7で割った余りに注目して計算する方法があります。
例えば、71×69＋67が7で割り切れるかは、
それぞれの数を7で割った余りの、1×6＋４＝10で調べることができます。
10は7で割り切れないので、もとの71×69＋67も7で割り切れません。
そうですね!!
やはり...いくらでも０にできますね ^^;...
またまた汚い Orz...添付図送付します~m(_ _)m~
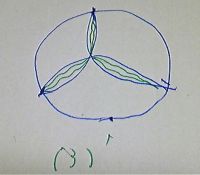
最初の(3)の右図においても...中にいくらでも周長の同じ線(緑)が描けるので...
3点が円周上にあろうが...一般に言えるわけですねぇ...Orz~
円周と同じ周長で円周上に点をとってできる図形の最小面積は・・・ですが、
この場合も、やはり、限りなく面積０にできるのではないかと思いますが・・・。
問１．
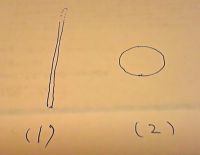
面積が等しくても周長は図1のようにすれば...いくらでも大きくなる。
そこで何処から見ても縦を短くすることを考えたら...円になることは予想できる...
問２．
同じく...添付図(1),(2) で...周長が等しくても面積は図1のようにすれば...限りなく0になる。
そこで...何処から見ても底辺を大きくすることを考えれば...円になることは予想できる...
あまりにアバウトすぎますか...^^;?
ついでに考えたこと...
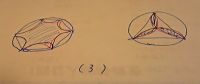
(A)添付図...(3)
周長が同じで面積が最小なものは 0に近づくが...円周と同じ周長で円周上に点をと
ってできる図形の最小面積は...(3) 図の右の図形ではないかと思ったもので...これ
って証明できないんでしょうかねぇ...?
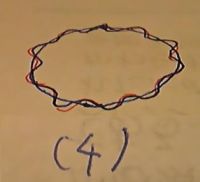
(B)添付図...(4)
面積が同じで周長が最大のものは限りなくあるが...円と同じ面積で円周上に点を取
ってできる図形を考えましたが...この場合は...(4)図のように...やはり、いくらで
も周長は大きくできるみたい...^^;...
これから(B)の対と考えられる(A)も...ひょっとしたら...いくらでも小さな面積の図
形ができるのかもしれません...?
数学の好きな大学生なら必ず知っている「Ｊｏｒｄａｎの閉曲線定理」と呼ばれる定理があります。
この定理は、「平面上の自己交差を持たないどんな閉曲線（いわゆる「輪っか」）も平面を「内側」と
「外側」に分ける。」というものです。高木貞治先生の有名な『解析概論』にも載っています。
この定理は、一見、当然（自明）と思えますが、実際に証明するのは非常に難しいものとして知られています。
今回は、この定理の証明ほど難しくはありませんが、やはり当然と思え、それでいて証明は難しい問題を提示します。
閉曲線の一つ、円についての問題です。
問１．面積が等しい全ての平面領域のうち、周長が最小となるのは円であることを証明してください。
問２．周長が等しい全ての平面領域のうち、面積が最大となるのは円であることを証明してください。
