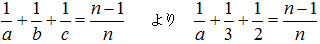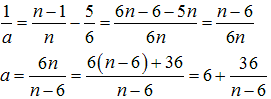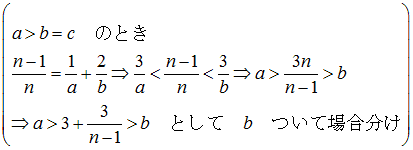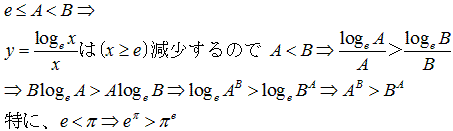NO.1905 当然と思える問題・その1(3) 2011.1.16. 夜ふかしのつらいおじさん
●内接三角形について
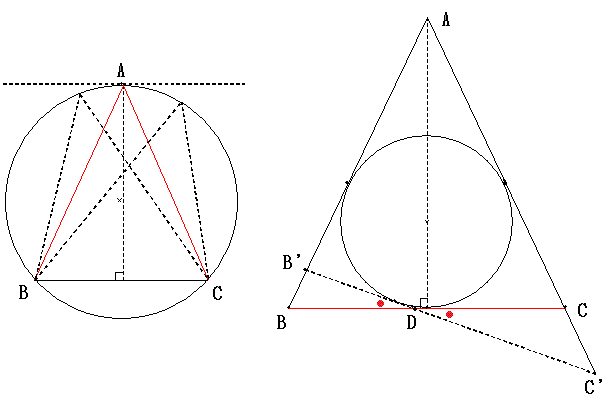
内接三角形の場合、底辺を固定して考えると面積の最大は二等辺三角形の場合です。
高さが一番高くなるからです。
どの辺を固定しても二等辺三角形であるのは正三角形です。
●外接三角形について
外接三角形の場合、底辺を固定して考えると面積の最小は二等辺三角形の場合です。
三角形の面積は2辺とその間の角の正弦の積で決まります。
図で△DBB'と△DCC'を比べて、Dのところの角は向かいあっているので等しいですが、
DB<DC、DB'<DC'は明らかなので、△DBB'<△DCC'です。
どの辺を固定しても二等辺三角形であるのは正三角形です。
NO.1904 当然と思える問題・その1(2) 2011.1.16. スモークマン
問1.
円内に1本の弦を考えるとき、それを底辺に下△の面積が最大になるときは…円の中
心を通る高さが最大なので…つまりは…二等辺三角形。このことは、どの辺において
もいえることなので…3辺に関して二等辺三角形のとき=正三角形のときの面積が最
大といえる。
あるいは…最初の操作を等辺を底辺にして繰り返して行った極限は正三角形になるこ
とは想像に難くない。
問2.
円外の点からその円への2本の接線の長さは同じ。
S=absinθ/2
だから…円外の3点から、それぞれ他の2点までの距離が等しく短い程よい。
どの3点からも同じときが最小のはずだから…
a=b=c のとき。
NO.1903 e と π について(4) 2011.1.16. K.F.
次の指数関数不等式
eX ≧ 1+X ・・・式.1
が成り立つのは明らかである。
(y=ex、y=1+xのグラフを描くことと、微分法により簡単に証明できる。)
式.1 のXに、X=(x-e)/e を代入すると、
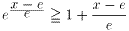 ・・・式.2
・・・式.2
を得る。ただし、式.2の等号が成立するのは、x=eのときのみである。
式.2の不等式を整理すると、
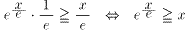 ・・・式.3
・・・式.3
を得る、ここで、式.3の右側の不等式の x 乗根をとると、
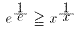 ・・・式.4
・・・式.4
を得る。よって、xが正の変数ならば、x1/x は、x=eのときに最大となる。
式.4にx=πを代入し、かつ両辺を eπ 乗 すると、e<πだから、
eπ > πe
NO.1902 遺言の問題(4) 2011.1.1. 夜ふかしのつらいおじさん
●ラクダ全体17頭を残さずに1/2、1/3、1/9に分けることはできません。
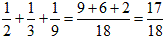 となるからです。
となるからです。
全体を残さずに1/2:1/3:1/9の比に分けることはできます。
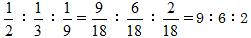 ですが、9+6+2=17となり、めでたしめでたしです。
ですが、9+6+2=17となり、めでたしめでたしです。
【前半】
●さて、賢者のラクダ1頭を加えて 頭のラクダを1/a、1/b、1/cに分けると、
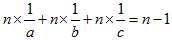 より次の式が導かれます。
より次の式が導かれます。
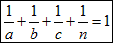 ・・・(※)
・・・(※)
(※)について調べます。
a、b、cは、1より大きい整数とします。
● 3数が等しいとき(a=b=c)、
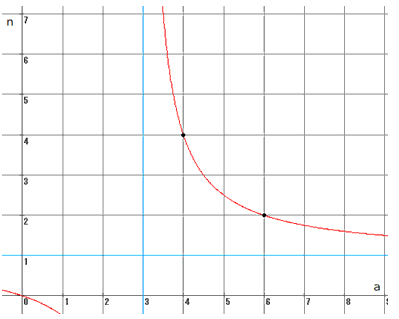
(a,n)は、(4,4)と(6,2)がが正の整数になりますが、後者は捨てます。
(1頭を分けることになるからです)
ラクダが3頭いて、1/4、1/4、1/4ずつ分けることになります。
● 2数が等しいとき(a=b)、
a=2 とすると、n=-c となり、うまくありません。
a を順に、3、4、5、6、(7)、8、(9)、(10)、(11)、12、(13)、・・・として考えます。
( )は解がないので省きます。
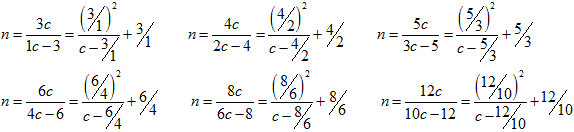
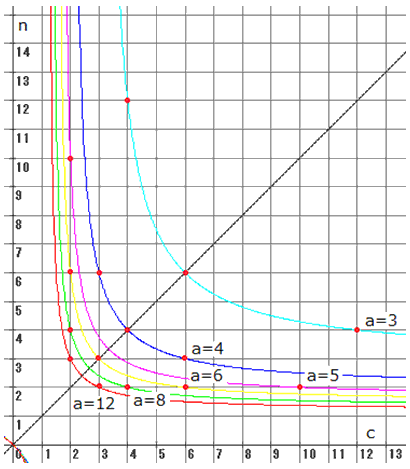
(n,c) は、
(空色)a=3 のとき、(4,12),(6,6),(12,4)
(青色)a=4 のとき、(3,6),(4,4),(6,3)
(紫色)a=5 のとき、(2,10),(10,2)
(黄色)a=6 のとき、(2,6),(3,3),(6,2)
(黄緑)a=8 のとき、(2,4),(4,2)
(赤色)a=12 のとき、(2,3),(3,2)
これらは、順に
(空色)ラクダが11頭いて、1/3、1/3、1/4に分ける、ラクダが5頭いて、1/3、1/3、1/6に分ける、不適当、
(青色)不適当、ラクダが3頭いて、1/4、1/4、1/4に分ける、不適当、
(紫色)ラクダが9頭いて、1/5、1/5、1/2に分ける、不適当、
(黄色)ラクダが5頭いて、1/6、1/6、1/2に分ける、不適当、不適当
(黄緑)不適当、 不適当
(赤色)不適当、 不適当
a=7,9,10,11,13、a>13のとき解がないのは、次の図から納得できます。
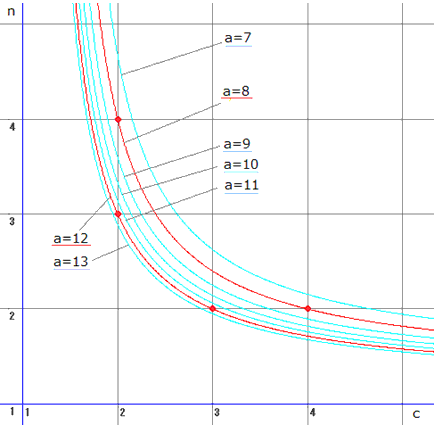
● 3数が異なるとき、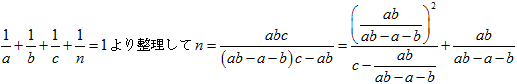
このペースでこの先に進むのは面倒なので止めます。
【後半】(a,b,cが異なるとして)
●4つの単位分数の和が1になることを考えます。(分子が1の分数を単位分数といいます)
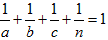
少なくともnはa,b,cの公倍数なので、a<b<c≦nとします。
単位分数は、自然数の逆数なので分母が小さいほど大きくなります。
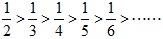
さて、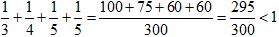
よりa<b<cの場合は、a=2でなくてはなりません。また、
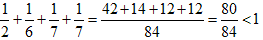
よりa=2のとき、bは3、4、5のどれかです。
●具体的に解いていきます。
・a=2、b=3のとき、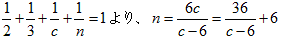
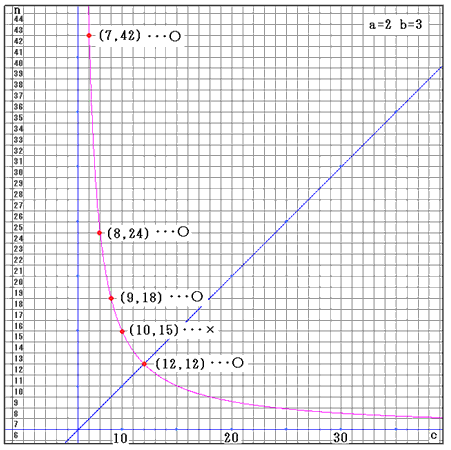
c≦nで、nがa,b,cの公倍数のものを選ぶと、
(c,n)は、(7,42)、(8,24)、(9,18)、(12,12)なので、
ラクダが41頭いて、1/2、1/3、1/7に分ける、ラクダが23頭いて、1/2、1/3、1/8に分ける、
ラクダが17頭いて、1/2、1/3、1/9に分ける、ラクダが11頭いて、1/2、1/3、1/12に分けるとなります。
・a=2、b=4のとき、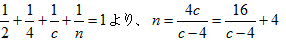
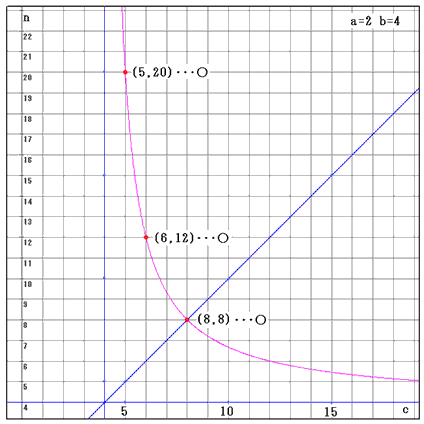
c≦nで、nがa,b,cの公倍数のものを選ぶと、(c,n)は、(5,20)、(6,12)、(8,8)、なので、
ラクダが19頭いて、1/2、1/4、1/5に分ける、ラクダが11頭いて、1/2、1/4、1/6に分ける、
ラクダが7頭いて、1/2、1/4、1/8に分けるとなります。
・a=2、b=5のとき、
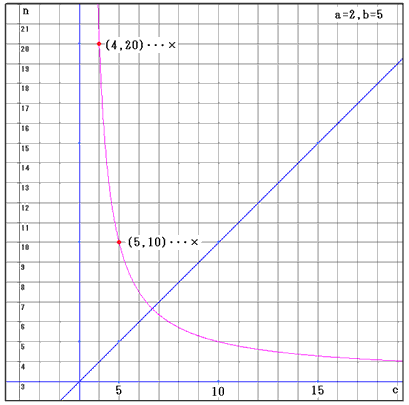
c≦nで、nがa、b、cの公倍数のものがないので、a=2、b=5のとき解がありません。
また、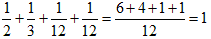
よりa=2、b=3のときは、c≦12です。
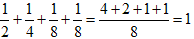
よりa=2、b=4のときは、c≦8です。
●まとめ
・3頭を1/4、1/4、1/4、
・11頭を1/3、1/3、1/4、 5頭を1/3、1/3、1/6、 9頭を1/2、1/5、1/5、 5頭を1/2、1/6、1/6、
・41頭を1/2、1/3、1/7、 23頭を1/2、1/3、1/8、 17頭を1/2、1/3、1/9、 11頭を1/2、1/3、1/12
19頭を1/2、1/4、1/5、 11頭を1/2、1/4、1/6、 7頭を1/2、1/4、1/8
以上12通りなので、有限個の解。
また、a、b、cが異なるときは2が必要。
【オマケ】
●単位分数を単位分数の和に直すこと
・次の式より、分子が2の規約分数を単位分数の和に直すことができます。
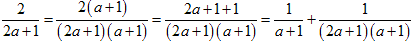
・また、分母が偶数の単位分数は、次のように変形すれば2つの単位分数の和に直せる場合があります。
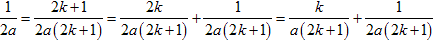
(3を分母、分子に掛ければ必ず2つの単位分数の和に直せます)
例えば、
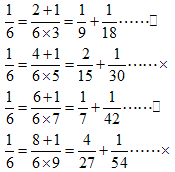
つまり単位分数に分けるのはただ1通りとはいえません。
もし、2個にこだわらなければ、×のものは、
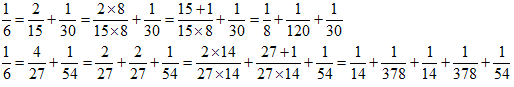
NO.1900 遺言の問題(2) 2011.1.11. スモークマン
ただひたすら計算...^^;...
n(ab+bc+ca)=(n-1)abc
1/a+1/b+1/c=1-1/n
1/a+1/b+1/c+1/n=1
1<a≦b≦c≦n
4/n ≦ 1
n ≧ 4
3/a ≧ 1-1/n ≧ 3/4
3/a ≧ 3/4
a ≦ 4
a=4 のとき…
1/b+1/c=3/4-1/n
2/b ≧ (3n-4)/4n
4 ≦ b ≦ 8n/(3n-4)
4(3n-4) ≦ 8n
4n ≦ 16
n ≦ 4
つまり…
1/4+1/4+1/4+1/4=1
a=3 のとき…
1/b+1/c=2/3-1/n
2/b ≧ (2n-3)/3n
3 ≦ b ≦ 6n/(2n-3) =3+9/(2n-3) ≦ 3+9/5
から…
b=3,4
1/3+1/3+1/c+1/n=1
1/c=1/3-1/n
c=3n/(n-3)=3+9/(2n-3) ≦ 3+9/5
c=3,4
a=b=c=3 は不適にて…
1/n=1-(1/3+1/3+1/4)=1/12
n=12
1/3+1/4+1/c+1/n=1
1/c=5/12-1/n
4 ≦ c=12n/(5n-12)
4(5n-12) ≦ 12n
8n ≦ 48
4 ≦ n ≦ 6
1-(1/3+1/4+1/4)=1/6
つまり…
1/3+1/4+1/4+1/6=1
1-(1/3+1/4+1/5)=23/69…不適
1-(1/3+1/4+1/6)=1/4…上と同じ。
a=2 のとき…
1/b+1/c=1/2-1/n
2/b ≧ (n-2)/2n
2 < b ≦ 4n/(n-2)=4+8/(n-2) ≦ 4+8/2=8
b=3,4,5,6,7,8
1/2+1/3+1/c+1/n=1
1/c+1/n=1/6
2/c ≧ 1/6
c ≦ 12
c=3,4,5,6,7,8,9,10,11,12
1-(1/2+1/3+1/3) < 0
1-(1/2+1/3+1/4) < 0
1-(1/2+1/3+1/5) < 0
1-(1/2+1/3+1/6)=0
1-(1/2+1/3+1/7)=1/42…◯
1-(1/2+1/3+1/8)=1/24…◯
1-(1/2+1/3+1/9)=1/18…◯
1-(1/2+1/3+1/10)=1/15…◯
1-(1/2+1/3+1/11)=5/66…X
1-(1/2+1/3+1/12)=1/12
1-(1/2+1/4+1/4)=0
1-(1/2+1/4+1/5)=1/20…◯
1-(1/2+1/4+1/6)=1/12…◯
1-(1/2+1/4+1/7)=3/28…X
1-(1/2+1/4+1/8)=1/8
1-(1/2+1/4+1/9)=5/36…X
1-(1/2+1/4+1/10)=3/20…X
1-(1/2+1/4+1/11)=7/44…X
1-(1/2+1/4+1/12)=1/6
1-(1/2+1/5+1/5)=1/10
1-(1/2+1/5+1/6)=2/15…X
1-(1/2+1/5+1/7)=1/5
1-(1/2+1/5+1/8)=7/40…X
1-(1/2+1/5+1/9)=17/90…X
1-(1/2+1/5+1/10)=3/5…X
1-(1/2+1/5+1/11)=23/110…X
1-(1/2+1/5+1/12)=13/60…X
1-(1/2+1/6+1/6)=1/6
1-(1/2+1/6+1/7)=4/21…X
1-(1/2+1/6+1/8)=5/24…X
1-(1/2+1/6+1/9)=2/7…X
1-(1/2+1/6+1/8)=5/24…X
1-(1/2+1/6+1/9)=2/9…X
1-(1/2+1/6+1/10)=7/30…X
1-(1/2+1/6+1/11)=8/33…X
1-(1/2+1/6+1/12)=1/4
1-(1/2+1/7+1/7)=3/14…X
1-(1/2+1/7+1/8)=13/56…X
1-(1/2+1/7+1/9)=31/126…X
1-(1/2+1/7+1/10)=9/35…X
1-(1/2+1/7+1/11)=31/154…X
1-(1/2+1/7+1/12)=23/84…X
1-(1/2+1/8+1/8)=1/4
1-(1/2+1/8+1/9)=19/53…X
1-(1/2+1/8+1/10)=11/40…X
1-(1/2+1/8+1/11)=25/88…X
1-(1/2+1/8+1/12)=7/24…X
後半は…それまでに出てるものがあれば省けそう…
a<b<c<n なら…以上の◯の6個しかない
これは計算でだしたけど…
2進法に関係してる気がする…^^;?
疲れたぁ~~~^^;v
NO.1899 当然と思える問題・その1 2011.1.11. K.F.
数学の勘が少しよい人なら瞬時に結論がわかる、でも証明は難しい、いわば当然と思える問題があります。
今回は、三角形についての問題です。
問1. 円に内接する三角形のうち、面積が最大となるのは正三角形であることを証明してください。
問2. 円に外接する三角形のうち、面積が最小になるのは正三角形であることを証明してください。
NO.1898 2種類のタイルで 2011.1.11. 水の流れ
第252回数学的な応募問題
ここに、1辺の大きさが3と4の2種類の正方形のタイルが合わせて2011個あります。
これらのタイルをうまく利用して、1辺の大きさがMの正方形の床にびっしりと隙間まく敷き詰めることが可能か
どうか考えてください。もし、可能なら大きさMの値と、
2種類のタイルをそれぞれ何個利用したかを教えてください。
また、1辺の大きさがMの正方形の床を1辺の大きさが3と4の2種類の正方形のタイルで敷き詰めることが可能ならば、
Mのもつ条件を考えてください。
「ピーター・フランクルの中学生でも分かる大学生にも解けない数学問題集②」から改題して出題しました。
敷き詰めることが可能な場合どのようにして2011個のタイルを張っていくかは私には一部の場合しか分かっていません。
注:この記事に関する投稿の掲載は、2011年1月31日以降とします。
NO.1895 遺言の問題 2011.1.1. 数学マニア
よく知られている問題で、遺言でラクダ17匹を、
3人で 1/2,1/3,1/9 に分けるのですが、そのままだと分けられなくて、1頭加えることで、うまく分けられるというお話です。
整数の方程式として考えると、
n(ab+bc+ca)=(n-1)abc
の整数解をとくことになると思います。
解は有限個でしょうか?また、必ず2が必要でしょうか?
N=12のとき、a=6,b=4,c=2
N=18のとき、a=9,b=3,c=2
N=20のとき、a=5,b=4,c=2
N=24のとき、a=8,b=3,c=2

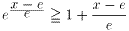 ・・・式.2
・・・式.2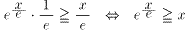 ・・・式.3
・・・式.3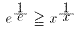 ・・・式.4
・・・式.4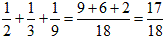 となるからです。
となるからです。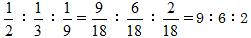 ですが、9+6+2=17となり、めでたしめでたしです。
ですが、9+6+2=17となり、めでたしめでたしです。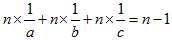 より次の式が導かれます。
より次の式が導かれます。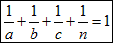 ・・・(※)
・・・(※)


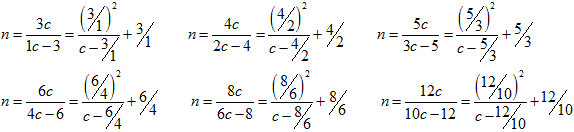


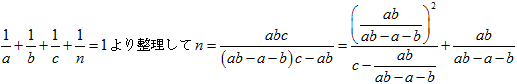
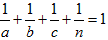
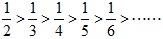
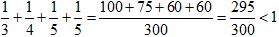
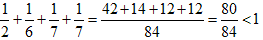
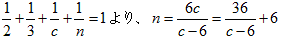

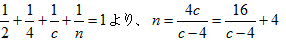


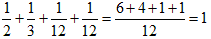
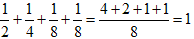
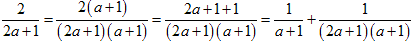
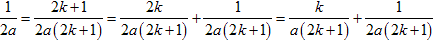
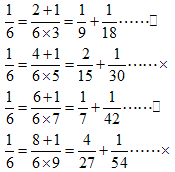
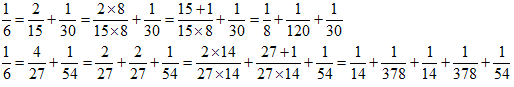
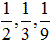 に分けるのですが、そのままだと分けられなくて、1頭加えることで、うまく分けられるというお話です。
に分けるのですが、そのままだと分けられなくて、1頭加えることで、うまく分けられるというお話です。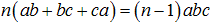
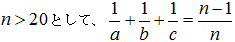 が成り立つがc=2でないとする。
が成り立つがc=2でないとする。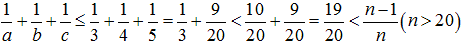 となり矛盾する。
となり矛盾する。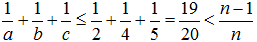 となり矛盾する。
となり矛盾する。