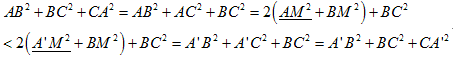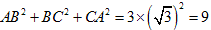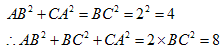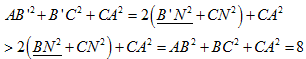NO.1877 数論の問題(3) 2010.9.20. スモークマン
表せる数 mを、ある数 k>0 として...そこから連続してt個までで表せるとする...t>0
m=k(t+1)+t(t+1)/2
=(t+1)(k+t/2)
m は、t=2g or t+1=2g であればよい...g>0
m=(2g+1)(k+g) or 2gk+g(2g-1)=2g2+g(2k-1)=g(2g+2k-1)
つまり...
m=奇数*z...奇数>1
つまり...
mを2で割ったとき、3以上の奇数になる数...
つまり...
m=2n...n>0 という数だけは表せない...1,2,22,23,...
NO.1876 数論の問題(2) 2010.9.20. 夜ふかしのつらいおじさん
1からnまでの自然数の和は、 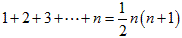 です。
です。
1からではなくkから始まるとすると、n個の各数に(k−1)を加えて、
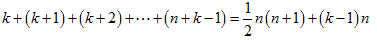 となります。
となります。
連続する数の和の表
| | 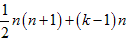
|
|---|
| k=1 | k=2 | k=3 | k=4 | k=5 | k=6 | k=7 | k=8 | k=9 | k=10
|
|---|
| 1 | 1 | 2 | 3 | 4
| 5 | 6 | 7 | 8 | 9 | 10
|
|---|
| 2 | 3 | 5 | 7 | 9 | 11
| 13 | 15 | 17 | 19 | 21
|
|---|
| 3 | 6 | 9 | 12 | 15 | 18
| 21 | 24 | 27 | 30 | 33
|
|---|
| 4 | 10 | 14 | 18 | 22 | 26
| 30 | 34 | 38 | 42 | 46
|
|---|
| 5 | 15 | 20 | 25 | 30 | 35
| 40 | 45 | 50 | 55 | 60
|
|---|
| 6 | 21 | 27 | 33 | 39 | 45
| 51 | 57 | 63 | 69 | 75
|
|---|
| 7 | 28 | 3 | 42 | 49 | 56
| 63 | 70 | 77 | 84 | 91
|
|---|
| 8 | 36 | 44 | 52 | 60 | 68
| 76 | 84 | 92 | 100 | 108
|
|---|
| 9 | 45 | 54 | 63 | 72 | 81
| 90 | 99 | 108 | 117 | 126
|
|---|
| 10 | 55 | 65 | 75 | 85 | 95
| 105 | 115 | 125 | 135 | 145
|
|---|
(n=1の欄は、1個の自然数の和ということなので自然数そのものになります)
例えば、k=5、n=7の欄の56は、5から始まる7個の自然数の和が56ということです。
この表のn=2以下の欄をみていくと、{1,2,4,8,16,・・・}などの数( のタイプ)が出てきません。
このうち、{1,2,4}などは試してみれば、複数個の連続する自然数の和で表せないのは納得できると思います。
連続する自然数の場合分けの表
| | 連続する個数
|
|---|
| 4k | 4k+1 | 4k+2 | 4k+3
|
|---|
| 始まりの数 | 奇数 | (1) | (3) | (5) | (7)
|
|---|
| 偶数 | (2) | (4) | (6) | (8)
|
|---|
連続するいくつかの自然数のパターンは、上のように分類できます。
例えば
(1)は、{1,2,3,4}、{1,2,3,4,5,6,7,8}
(2)は、{2,3,4,5,}、{2,3,4,5,6,7,8,9}
(3)は、{1,2,3,4,5}、{1,2,3,4,5,6,7,8,9,}
(4)は、{2,3,4,5,6}、{2,3,4,5,6,7,8,9,10}
(5)は、{1,2}、{1,2,3,4,5,6}
(6)は、{2,3}、{2,3,4,5,6,7}
(7)は、{1,2,3}、{1,2,3,4,5,6,7}
(8)は、{2,3,4}、{2,3,4,5,6,7,8}などです。
2p には、2しか因数にありません。
連続する偶数個の自然数の和は、両端の数の和と個数の半分の数の積で決まります。
(1)と(2)は、両端の数の和が奇数です。
例えば、(1)の数の和は、5×2=10、9×4=36、(2)の数の和は、7×2=14、11×4=44のように少なくとも1個の奇数を因数に持ちます。
だから、(1)、(2)のパターンでは、2p になりえません。
(5)と(6)は、両端の数の和が奇数で個数の半分も奇数です。
例えば、(5)の和は、3×1=3、7×3=21、(6)の和は、5×1=5、9×3=27のように基本的に2個の奇数を因数に持ちます。
(個数が2個の場合奇数の因数は最低で1個です)
だから、(5)、(6)のパターンでは、2p になりえません。
連続する奇数個の自然数の和は、中央の数と個数の積で決まります。
(3)と(8)は、中央の数が奇数で、個数も奇数個です。
例えば、(3)の和は、3×5=15、5×9=45、(8)の和は、3×3=9、5×7=35のように少なくとも2個の奇数を因数に持ちます。
だから、(3)、(8)のパターンでは、2p になりえません。
(4)と(7)は、中央の数が偶数で、個数が奇数個です。
例えば、(4)の和は、4×5=20、6×9=54、(7)の和は、2×3=6、4×7=28のように少なくとも1個の奇数を因数に持ちます。
だから、(4)、(7)のパターンでは、2p になりえません。
以上から 2p パターンの自然数は、連続するいくつかの自然数の和で表すことができません。
NO.1875 数論の問題 2010.9.16. K.F.
問1 ほとんど全ての自然数は、連続したいくつかの自然数の和として表されます。
例:15=1+2+3+4+5=7+8
ところが、そう表すことができないタイプの数が1種類だけあります。
その数を見付けてください。
問2 問1の数が、連続したいくつかの自然数の和で表すことができないことを証明してください。
NO.1873 積が和の2010倍 2010.9.6. 水の流れ
第246回数学的な応募問題
3350と5025の2数をとると、
3350+5025=8375 、 3350×5025=16833750=8375×2010
となり、積は和の2010倍となる。
このように、積が和の2010倍になる2数の組について、次の問に答えよ。
ただし、ここでの2数は自然数とする。
問1:2数の組は何組あるか。
問2:2数のうち和が最小の組と最大の組の2数を求めよ。
問3:すべての2数の組を求めよ。
問4:さらに、積が和のP倍として、考察があれば、書いてください。
注:この記事に関する投稿の掲載は、2010年9月27日以降とします。
NO.1872 円に内接する三角形(2) 2010.9.6. 夜ふかしのつらいおじさん
【あ】まず、中線定理(パップスの定理)の確認をします。
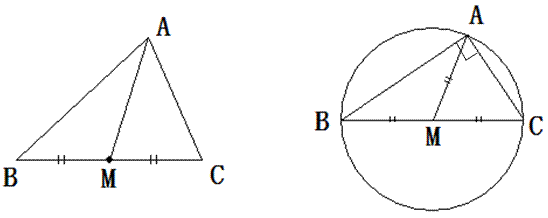
△ABCの中線をAMとすると、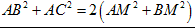 となります。
となります。
ついでに、∠A= 90°なら、点AがBCを直径とする円周上にあるので、
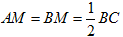 となります。
となります。
だから、
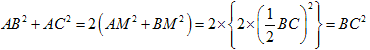 となり、
三平方の定理(ピタゴラスの定理)の形になります。
となり、
三平方の定理(ピタゴラスの定理)の形になります。
【い】円に内接する三角形は、辺BCを固定すれば、
その辺BCを底辺とする二等辺三角形のとき、三辺の平方和が最大となります。
これは、中線定理から確認できます。
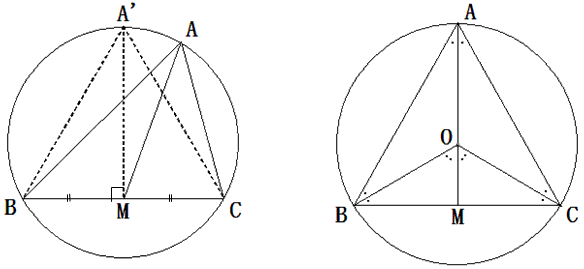
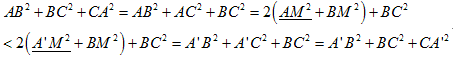
次に、辺A'Cを固定したとすれば、同様に、A'Cを底辺とする二等辺三角形のとき、三辺の平方和が最大となります。
このように考えれば、△ABCが正三角形のとき、三辺の平方和が最大となります。
(正三角形の場合どの辺を固定しても三辺の平方和をそれ以上の値にできません)
半径1の円に内接する正三角形の1辺の長さは √3 になります。
だから、 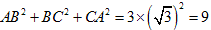
【う】半径1の円に内接する直角三角形は、各辺の平方和が8になります。
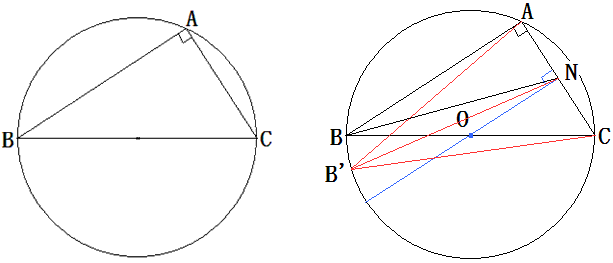
三平方の定理より
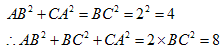
【え】円に内接する鋭角三角形は、各辺の平方和は8より大きくなります。
鋭角三角形 AB'C について、
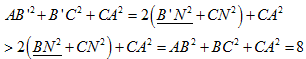
問題(1)上の【え】の内容から、
AB2+BC2+CA2>8ならば△ABCは鋭角三角形です。
問題(2)上の【い】の内容から、
AB2+BC2+CA2≦9となります。
等号は正三角形の場合です。
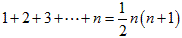 です。
です。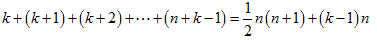 となります。
となります。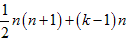
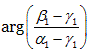 だけ動かした点を α2 とする。つまり、式にすると
だけ動かした点を α2 とする。つまり、式にすると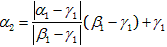
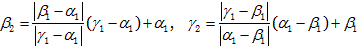 を得る。
を得る。
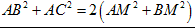 となります。
となります。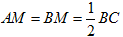 となります。
となります。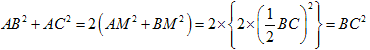 となり、
三平方の定理(ピタゴラスの定理)の形になります。
となり、
三平方の定理(ピタゴラスの定理)の形になります。