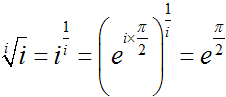NO.1867 正五角形の問題 2010.7.25. K.F.
正五角形が定規とコンパスだけで作図可能な多角形だということは、
古代ギリシアの時代から知られています。今回は正五角形の問題です。
問1
正五角形を利用して、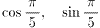 の値を求めよ。
の値を求めよ。
 問2
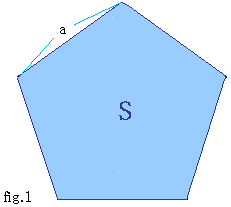
問2
一辺の長さが、aの正五角形の面積Sを求めよ。
 問3
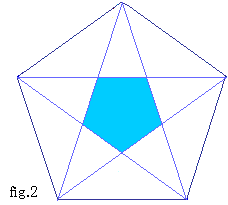
問3
正五角形の各頂点を結ぶと、正五角形の内側に小さな正五角形ができる。
外側の正五角形と内側の正五角形の面積比を求めよ。
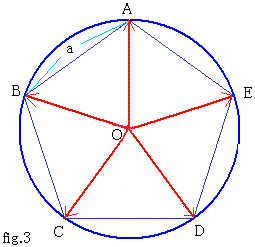 問4
問4
正五角形の外接円を考える。
外接円の中心をO、正五角形の各頂点を、A、B、C、D、Eとする。
(1) 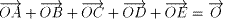 を証明せよ。
を証明せよ。
(2) 正五角形の一辺の長さがaのとき、  の値を求めよ。
の値を求めよ。
問5
12枚の正五角形によって、正十二面体がつくられる。
一辺の長さがaの正十二面体の体積を求めよ。
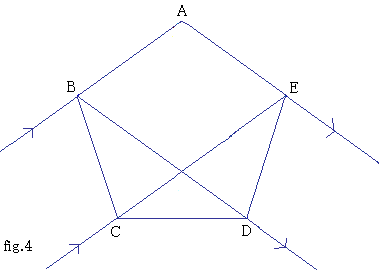 問6
問6
割りばしの袋のように幅が短く平行な平面をひとひねりすると、fig.4のような図形ができる。
このとき、多角形ABCDEが正五角形になることを証明せよ。
NO.1866 正三角形の問題 2010.7.14. 水の流れ
第244回数学的な応募問題
平成13年の岡山大学入試問題を見ていると、次のような問題が出ていました。
問題:原点を中心とする半径1の円が座標平面上にある。この円に内接する正三角形を
原点を中心に回転させるとき、この正三角形の第1象限にある部分の面積の最小値と最大値を求めよ。
注:この記事に関する投稿の掲載は、2010年8月9日以降とします。
NO.1865 包絡線(2) 2010.7.14. DDT
実数条件問題と言われる出題だと思います(←言い方が古いですか?)。自分が受験生の頃は、北大がこの手の問題のメッカでした。
問題1.
与式をtについて整理し、その左辺をf(t)とおく。
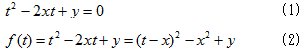
(1)が0≦t≦1に解を持つためには、(2)において以下の条件が成り立てば良い。
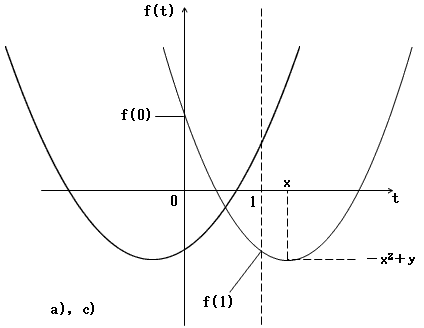
a)x≦0の時
f(0)=y≦0 かつ f(1)=y-2x+1≧0
b)0< x<1の時
f(0)=y≧0 または f(1)=y-2x+1≧0
c)1≦xの時
f(0)=y≧0 かつ f(1)=y-2x+1≦0
d)実数条件
(a),(b),(c)いずれに対しても、
かつ y-x2≦0
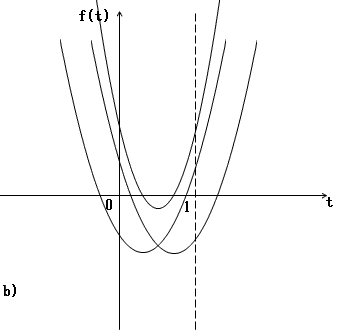
a)〜d)より、次が得られる。
ハッチ部が、(x,y)の通過領域。境界を全て含む。
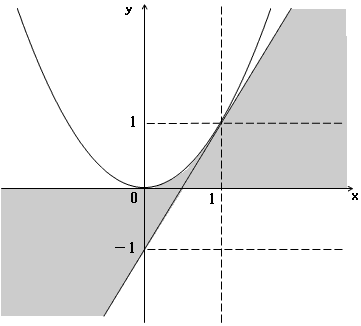
問題2.
点A=(0,t2+4)と点B=(t/2+2/t、0)を結ぶ線分は、0≦k≦1として、以下で与えられる。
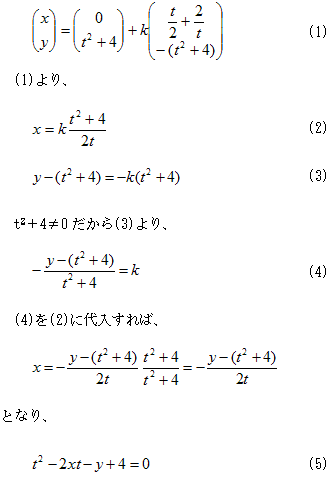
が得られる。(5)の左辺をf(t)とすれば、
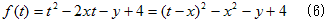
(5)が0<t<2に解を持つ条件は、問題1.と同様に、(6)において以下となる。
a)x≦0の時
f(0)=-y+4<0 かつ f(2)=-y-4x+8>0
b)0< x<2の時
f(0)=-y+4>0 または f(2)=-y-4x+8>0
c)2≦xの時
f(0)=-y+4>0 かつ f(2)=-y-4x+8<0
d)実数条件
(a),(b),(c)いずれに対しても、
かつ -y-x2+4≦0
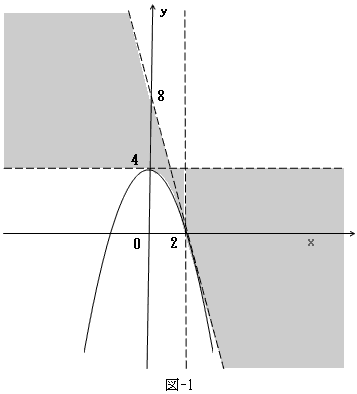
a)〜d)より、上図のハッチ部となるが、0≦k≦1となるか、チェックする。それは図-1の領域上において、(t,k)を領域上に導入された内部座標と考え、(t,k)=(0,k),(2,k),(t,0),(t,1)のラインを考えれば良い。任意の(0,k),(2,k)については、図-1の領域の境界として既に得られている。後は、k=0,1のラインを定めるのみ。
k=0として、任意の0<t<2に対して、点Aは、
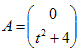
なので、必ずy軸上にあり、y成分はtについて単調増加だから、Aのy座標は、4<y<8の範囲。
k=1として、任意の0<t<2に対して、点Bは、
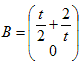
となるが、x成分をg(t)とおけば0<t<2に対して、
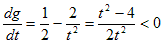
となり、x成分はtに関して単調減少。また、
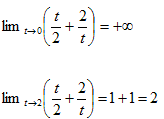
より、Bは必ずx軸上にあり、x座標の範囲は2<x。従って下図となる。ただし境界は赤線部のみ含み、白丸は含まない。図-2の線分ABで、0≦k≦1が成り立つのは、以上とkの定義より明らか。
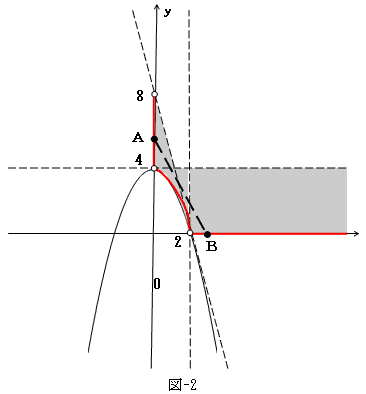
問題3.
与式、
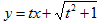 (1)
(1)
より(x,t)を、求める領域の点(x,y)を表わす内部座標と考える。0<t。
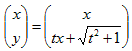 (2)
(2)
(2)において、
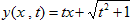 (3)
(3)
と表わす。
0≦xのとき、(3)はtについて単調増加。また、
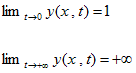
だから、0≦xかつ0<tで(x,y)全体は、1<y。
x<0とする。
(1)のtxを移項し、両辺を2乗すれば、
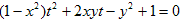 (4)
(4)
が得られる。(1)より得られる拘束条件は以下。
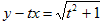 (5)
(5)
例によって、(4)の左辺をf(t)とおく。
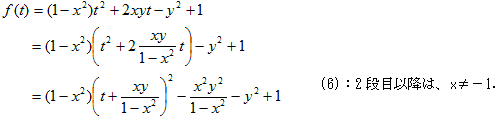
a)−1<x<0の時
a-1) −xy/(1−x2)≦0 ⇒ 0≦xyの時
f(0)=-y2+1<0
y<−1または1<y。
a-2) 0<−xy/(1−x2) ⇒ xy<0の時
f(t)=0は、次のa-3)が満たされれば、必ず0<tに解を持つ。
a-3) 実数条件
a-1),a-2)いずれに対しても、
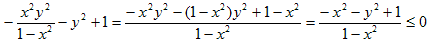
だが、−1<x<0だから、
x2+y2≧1
b) x=−1の時
この時(6)の1段目は、
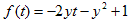
になる。y=0の場合f(t)=1なので、f(t)=0は不可能。従ってy≠0。y≠0とすると、
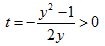
となります。
b-0) y≠0
b-1) 0<y ⇒ 0<y<1
b-2) y<0 ⇒ y<−1
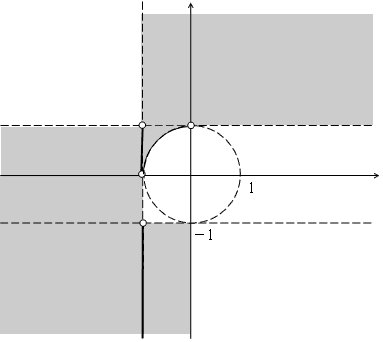
C)x<−1の時
c-1) −xy/(1−x2)≦0 ⇒ xy≦0の時
f(0)=-y2+1>0
-1<y<1。
c-2) 0<−xy/(1−x2) ⇒ 0<xyの時
f(t)=0は、次のc-3)が満たされれば、必ず0<tに解を持つ。
c-3) 実数条件
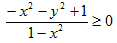
だが、x<−1だから、
x2+y2≧1
以上をまとめると、右図。
拘束条件(5)を考慮する。(5)より、
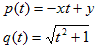
の交点の存在が必要。q(t)の概形を調べるために、両辺2乗すると、
(q-t)(q+t)=1
なので、
r=q-t
s=q+t
とすれば、
rs=1
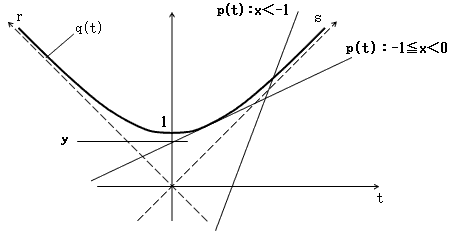
0<t,x<0,0<qで考えると、交点を持つ条件は図のようになる。p(t)とq(t)の接する条件は明らかに、
x2+y2=1
で、−1≦x<0のとき図より、
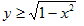
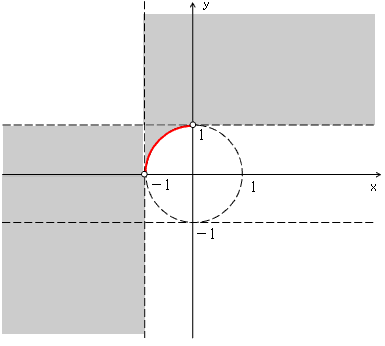
x<−1ならp(t)の傾きは、q(t)の暫近線sの傾きより大きくなるから、任意のyでp(t)とq(t)は、y=1を除き、0<tに交点を持つ。
従って、求める領域は下図。境界は赤線部のみ含み、白丸は含まない。
NO.1864 iのi乗(2) 2010.7.4. 夜ふかしのつらいおじさん
オイラーの公式 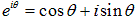 を使って考えると分かりやすくなります。
を使って考えると分かりやすくなります。
次の関係をみるとオイラーの公式を納得しやすいと思います。
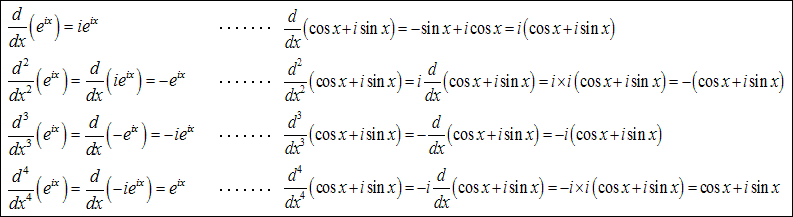
オイラーの公式において、θ=πとすると、 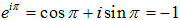 より
より
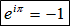 という美しいとされる式になります。
という美しいとされる式になります。
対数の底の変換の技術も必要です。 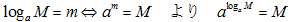
また、ド・モアブルの定理を知っていると計算をしなくてすみます。 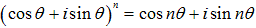
問1
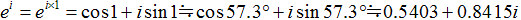
問2
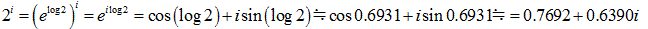
問3
オイラーの公式より、 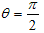 のとき、
のとき、 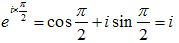 なので、底の方のiを書き換えると、
なので、底の方のiを書き換えると、
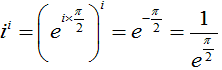
問4
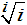 は
は
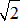 や
や
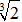 のようにわかりやすい数ではありません。
のようにわかりやすい数ではありません。
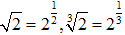 のように
のように
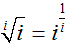 と考えることとします。
と考えることとします。
問題3と同じように、底の方の i を書き換えると、
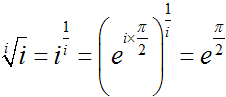
となり、問題3の逆数になります。
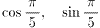 の値を求めよ。
の値を求めよ。
 問2
問2 問3
問3 問4
問4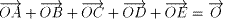 を証明せよ。
を証明せよ。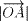 の値を求めよ。
の値を求めよ。 問6
問6




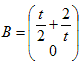
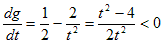
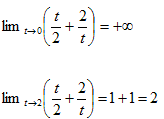

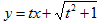 (1)
(1)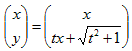 (2)
(2)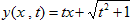 (3)
(3)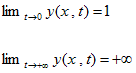
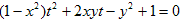 (4)
(4)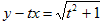 (5)
(5)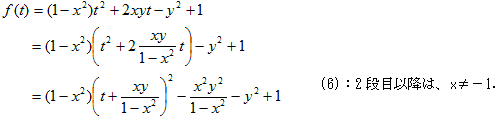
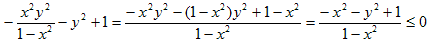
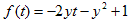
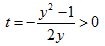

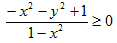
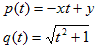

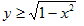

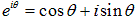 を使って考えると分かりやすくなります。
を使って考えると分かりやすくなります。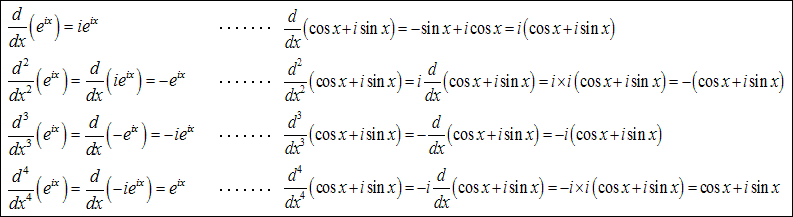
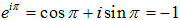 より
より
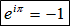 という美しいとされる式になります。
という美しいとされる式になります。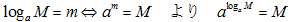
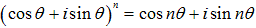
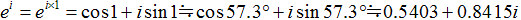
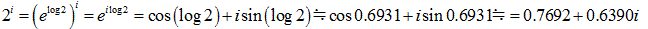
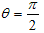 のとき、
のとき、 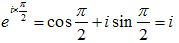 なので、底の方のiを書き換えると、
なので、底の方のiを書き換えると、
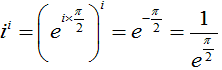
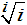 は
は
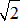 や
や
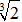 のようにわかりやすい数ではありません。
のようにわかりやすい数ではありません。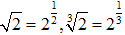 のように
のように
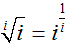 と考えることとします。
と考えることとします。