NO.1863 包絡線 2010.6.22. 水の流れ
第２４３回数学的な応募問題
大学入試問題を見ていると、次のような問題が出ていることがあります。紹介します。
注：この記事に関する投稿の掲載は、2010年7月12日以降とします。
NO.1862 完全数(3) 2010.6.22. Ryu1128
問題1
２ｎ−１の約数は２i（i=0〜n-1）・・・(1)
これは等比数列なのでその和は２ｎ−１・・・(2)
（２ｎ−１）は素数で２ｎ−１＜２ｎ−１なので
(1)に各々かけたものも異なる約数となりその和は
（２ｎ−１）（２ｎ−１）・・・(3)
(3) はもとの数も含んでいるので
２ｎ−１（２ｎ−１）の約数の総和は
(2)+(3)-２ｎ−１（２ｎ−１）=２ｎ−１（２ｎ−１）
よって完全数である。
問題2
分らなかったのでオイラーさんに聞いたら教えてくれました。自力ではないので降参です。
問題3
完全数6の約数1、2、3の約数の逆数を取り合計すると11/6となりますが？
題意がどうも分りません。自身も含むのでしょうか？それなら12/6＝2となり分るの
ですが・・・
とりあえず自身も含むとしてやってみます。
完全数Nの約数を全て並べると
ａ0, ａ1, ａ2, ａ3・・・・ａn-1
ａ0,=1 ａn-1＝N ・・・(1)
また
ａ0×ａn-1 ＝ａ1×ａn-2
＝ａ2×ａn-3 ＝ａ3×ａn-4 ＝・・・・＝ａi ×ａi+1＝N （ｉ＝ｎ/2-1）・・・(2)
ａ0×ａn-1 ＝ａ1×ａn-2
＝ａ2×ａn-3 ＝ａ3×ａn-4 ＝・・・・＝ａi2＝N （ｉ＝(n-1)/2）・・・(2)'
なので約数の逆数の総和は
（ａ0+ａn-1）/Ｎ+（ａ1+ａn-2 ）/Ｎ・・・・+（ａi＋ａi+1）/Ｎ・・・(3)
（ａ0+ａn-1）/Ｎ+（ａ1+ａn-2 ）/Ｎ・・・・+（2ａi）/Ｎ・・・(3)'
ここでＮは完全数なので
（ａ0+ａ1+ａ2+ａ3・・・・+ａn-2）＝Ｎ
結局(3)は
（Ｎ+Ｎ）/Ｎ＝2
となります。
問題4
ｐ、ｑが奇素数でpqが完全数ならば
1+ｐ+ｑ＝ｐｑ・・・(1)
が成り立つ。変形すると
（ｐ-1）（ｑ-1）＝2・・・(2)
1を除く最小の奇素数は3で2番目に小さい奇素数は5
よって(2)の左辺は常に8より大きくなり(2)は成立しない
したがってｐｑは完全数とはならない。
あまりに安易な証明に不安を覚えます・・・
NO.1861 完全数(2) 2010.6.22. 夜ふかしのつらいおじさん
0 準備
・ Ｎ＝ｐm×ｑn の約数の個数は、（m＋１）×（n＋１）個 （ｐ、ｑは素数）
・ Ｎ＝ｐm×ｑn の約数は、次の展開の各項
（１＋ｐ＋ｐ2＋ｐ3＋･･･＋ｐm）
×（１＋ｑ＋ｑ2＋ｑ3＋･･･＋ｑn）
・ Ｎ＝ｐm×ｑn の約数すべての和は、
（１＋ｐ＋ｐ2＋ｐ3＋･･･＋ｐm）
×（１＋ｑ＋ｑ2＋ｑ3＋･･･＋ｑn）
・ Ｎ＝ｐm×ｑn が完全数かの判断は、
（１＋ｐ＋ｐ2＋ｐ3＋･･･＋ｐm）
×（１＋ｑ＋ｑ2＋ｑ3＋･･･＋ｑn）＝２×N が成立するかどうか
1 ２n-1×（２n−１）の約数の和は、
よって、２n-1×（２n−１）は完全数となります。
2 偶数の完全数は、因数分解すると、２n-1×（２K−１）の形になります。
・ ２Ｋ−１が素数のとき
完全数なのでこの値が２×２n-1×（２K−１）と等しいとして、
よって、２n-1×（２n−１）の形になります。
・ ２Ｋ−１＝（２ｐ−１）（２ｑ−１）のとき、（２ｐ−１と２ｑ−１は素数とします）
となり、完全数にはなりえません。
※ 奇数部分２K−１が３個以上の奇素数の積の場合も同様に考えることができます。
3 Ｎを偶数の完全数とします。
4 積ｐｑが完全数とすると、次の関係が成り立ちます。
このグラフをかくと、次のようになります。
（ｐ，ｑ）の組合せは、（２，３）と（３，２）だけですが奇素数のペアではありません。
NO.1860 ｉのｉ乗 2010.6.13. K.F.
複素関数論を勉強していたときに知った問題を提示します。
問１ ｅｉ（ｉは虚数単位）は複素数です。
複素数として具体的に式で表してください。
問２ ２ｉも複素数です。
複素数として具体的に式で表してください。
問３ ｉｉは実数になります。
実数として具体的に式で表してください。
問４ ご迷惑をおかけします。問題を訂正します。(2010.6.26.)
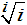も実数になります。
実数として具体的に式で表してください。
NO.1859 完全数 2010.6.1. 水の流れ
第２４２回数学的な応募問題
皆さん、６，２８，４９６，８１２８，次が 33550336 である数字が完全数である
とはご存知でしょう。完全数とは自分自身を除いた他のすべての正の約数の和がその数に一致している自然数をいいます。ここで、問題です。
問題１：２ｎ−１が素数ならば、２ｎ−１（２ｎ−１）は完全数であることを証明せよ。
問題２：偶数の完全数はすべて、２ｎ−１（２ｎ−１）の形にかけることを証明せよ。
このとき、ｎおよび２ｎ−１は素数である。
問題３：完全数Ｎのすべての正の約数について、その逆数をとり合計すると和が２になることを証明せよ。
問題４：ｐとｑが、異なる奇素数であるとき、積ｐｑは完全数でないことを証明せよ。
注：この記事に関する投稿の掲載は、2010年6月21日以降とします。
NO.1858 四角形の面積(4) 2010.6.1. 夜ふかしのつらいおじさん
□ABCDの面積は、△ABCと△CDAの和なので、
余弦定理から△ABCと△CDAとでACの２乗を求めると、
この２式の差をとると、
（あ）と（い）を２乗して加えると、
∠Ｂ＋Ｄ＝180°のとき、cos（B+D)＝−１となり四角形の面積が最大になります。
なお、この式で、ｄ＝０とすると三角形のヘロンの公式が導けます。
NO.1857 四角形の面積(3) 2010.6.1. 夜ふかしのつらいおじさん
□ＡＢＣＤの対角線ＡＣの長さをｘとおきます。
ｘはいろいろな値をとります。
この図の場合は、最大でA'Cの値、最小でA''Cの値になります。
a,b,c,d,xを用い、
ヘロンの公式で△ＡＢＣと△ＣＤＡの面積を求めます。
同様に
□ABCDの面積をｙとおくとｙは、ｘの関数になります。
ｘの定義域は、図１の場合、A''C＜ｘ＜A'Cです。
※ ｙをｘ2の関数とみるとよいと思います。
図１から想像できるように、定義域の両端でｙは小さな値をとります。
およそ、図２のような上に凸の曲線になります。
なお、この面積の式★の前半の値をｙとおくと、ｘ2とｙとには楕円の関係があります。
この面積の式★の最大値を求めます。
ｔ＝ｘ2とおきます。
面積の式をｔで微分して最大値を考えます。
ここで、［ ］の中が０として次のように変形します。
両辺を２乗して、
ここで、ｔについて解きます。
後ろの［ ］が０とすると、ａ，ｂ，ｃ，ｄの値によってはｔが負の値になります。
よって、前の［ ］が０として解くと、
このｔを面積の式に代入して最大値を求めます。
まず、前半の根号の中を計算します。
次に、後半の根号の中を計算します。
（式の性質を考えて、ａ，ｂはｃ，ｄに、ｃ，ｄはａ，ｂに置き換えます）
以上からｙの最大値は、
となります。
NO.1856 四角形の面積(2) 2010.6.1. ＤＤＴ
題意を、辺長a，b，c，dを変えないで面積を最大にせよ、という意味にとりました。
最初に本当にそんな事が出来るのか気になったので、問題の自由度を勘定します（例えば三角形だったら、不可能）。
四角形の頂点を2次元座標で表せば、2個の実数の組になるので、4頂点で8自由度。しかし四角形の形しか問題にならないので、1頂点の位置と、1辺の方向は固定できる。これらの自由度は3なので、8−3＝5自由度。
さらに辺長a，b，c，dが決まっているから、さらに4自由度減って、1自由度。つまり1個の自由度の範囲で四角形を変えられる。従って、面積最大には意味がある。しかし、その1自由度を何にするかで、解法の難易にかなり差が出そう・・・。
図を見ていたら、三角測量網の閉合計算を思い出しました。そこで三角網に分割し、角度θ1とθ2をトランシットで測ると仮定。基線eには、基線測量（長さを測る）を行う。余談ですが、基線測量は今では光波測距儀（レーダー）で行われますが、名人がJIS規格の鋼製巻尺を使うと、機械も裸足で逃げ出すくらいの精度が出ます。
・・・それはさておき。三角網を基線eで閉合します。余弦定理より、
不要な仮定eを消すために、(1)と(2)の辺々引けば、
さらに四角形の面積は、
で、拘束条件(3)のもとでのＡの最大化が目的。（(3)より、やっぱり自由度は1だ^^）
このあと測量計算の流れで、ラグランジュの未定定数法を使おうかと思ったのですが、(3)と(4)を見ていたら、2乗して足したくなりました。
結果は、
です。Ａの最大化を行うかわりに、(5)右辺の最大化を行っても同じです。凸四角形なので明らかに、
のとき、(5)の右辺は最大です。(6)を拘束条件(3)に代入すれば、
が得られます。
(7)の右辺は、−1〜1の範囲にある必要がありますが、これが四角形の閉合条件になるはずです。凸四角形なのでそのまま、
が閉合条件。(7)より、
閉合条件(8)より、中辺のルート内は正で、凸四角形なのでルートの符号は＋のみ。
(9)と(4)より、Ａの最大値は、
す。ただし閉合条件(8)を守るとします。
