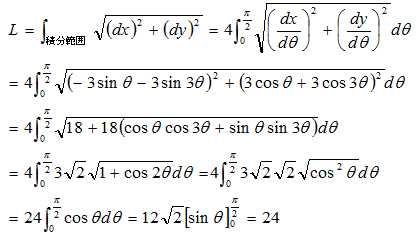NO.1815 6nー1の素数 2009.11.24. 水の流れ
皆さん、今年の千葉大学入試問題の中で、素数の関する問題がありました。
(1)5以上の素数は、ある自然数nをも用いて6n+1または6n−1の形に表されることを示せ。
(2)Nを自然数とする。6N−1は、6n―1(nは自然数)の形で表される素数を約数にもつことを示せ。
(3)6n―1(nは自然数)の形で表される素数は無限に多く存在することを示せ。
注:この記事に関する投稿の掲載は、2009年12月14日以降とします。
ColloquiumNO.249
|
皆さん、今年の千葉大学入試問題の中で、素数の関する問題がありました。
(1)5以上の素数は、ある自然数nをも用いて6n+1または6n−1の形に表されることを示せ。
(2)Nを自然数とする。6N−1は、6n―1(nは自然数)の形で表される素数を約数にもつことを示せ。
(3)6n―1(nは自然数)の形で表される素数は無限に多く存在することを示せ。
注:この記事に関する投稿の掲載は、2009年12月14日以降とします。
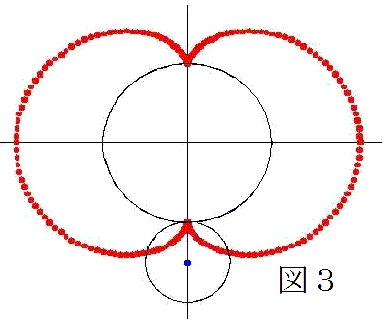
皆さん、1つの円が定直線に接しながら、滑ることなく回転するとき、円周上の定点の軌跡をサイクロイドといいます。そこで、定円に内接しながら円が滑らずに回転するときの円周上の定点の軌跡はホモサイクロイド言います。ここで、過去の早稲田大学の入試問題を紹介します。

注:この記事に関する投稿の掲載は、2009年11月23日以降とします。
問題1
図1の状態が最初です。(点Tは2円の最初の接点です)
∠COD=θ まで円Qが回転したとします。(図2)
弧CDの長さは、円Oの半径が2なので 2θです。
弧CD=弧CT なので∠CQT=2θです。
PTは円Qの直径で、またQX’とOXは平行なので、
∠PQX’=(2θ+π)−(π−θ)=3θ
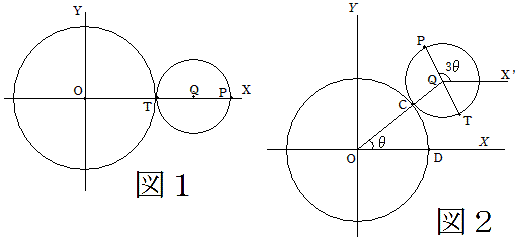
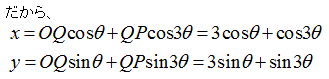
問題2
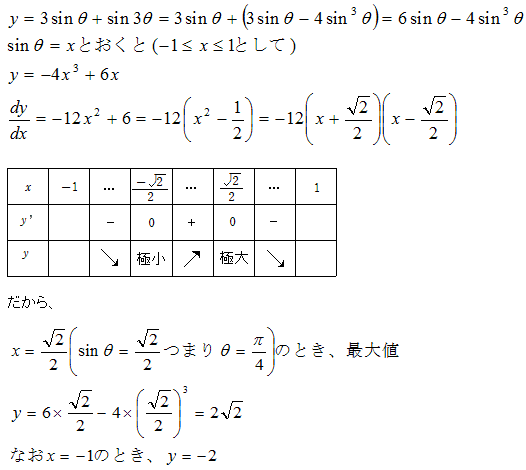
問題3