NO.1809 エピサイクロイド 2009.10.13. 水の流れ
皆さん、1つの円が定直線に接しながら、滑ることなく回転するとき、
円周上の定点の軌跡をサイクロイドといいます。
そこで、定円に外接しながら円が滑らずに回転するときの円周上の定点の軌跡はエピサイクロイド言います。
ここで、過去の福井医科大学の入試問題を紹介します。
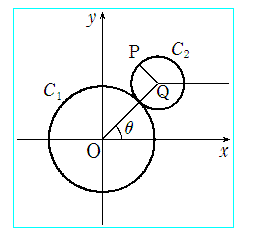
座標平面上に原点Oを中心とする半径２の円C１がある。半径１の円C２が
C１に外接しながら滑ることなく転がるとき、C２上の定点Pが描く曲線について考える。
C２の中心をQとし、Qが点（３，０）にあるとき、Pは点（４，０）にあるとする。
このとき、ｘ軸の正の方向から線分OQへ測った角をθとして次の問いに答えよ。
問題１：点Pの座標（ｘ，ｙ）をθで表せ。
問題２：０≦θ≦２πにおいてｙの最大値を求めよ。
問題３：θが０≦θ≦２πの範囲を動くとき、
点Pの描く曲線の長さを求めよ。
注：この記事に関する投稿の掲載は、2009年11月2日以降とします。
