ColloquiumNO.232
|
皆さん、過去の大学入試問題を見ていたら、下のような問題がでていました。
注：この記事に関する投稿の掲載は、２００８年７月14日以降とします。
【奇数乗和】
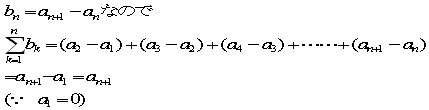
(1)
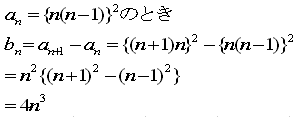
(2)
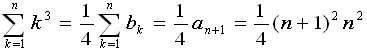
(3)
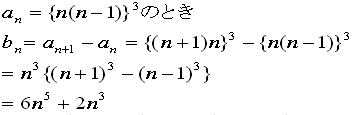
(4)
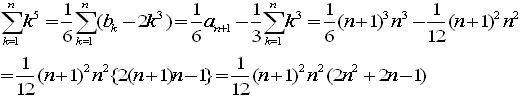
(5)
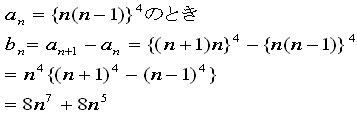
(6)
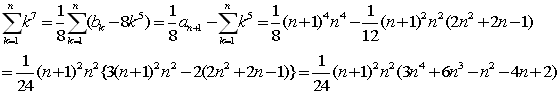
(7)
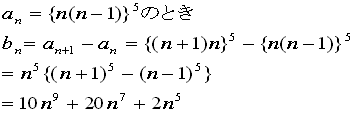
(8)
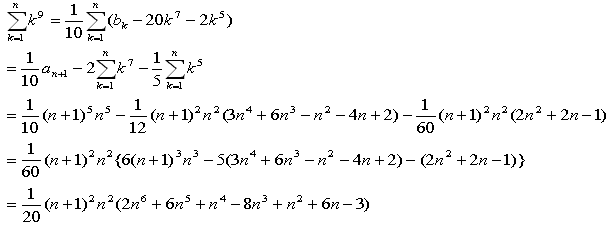
ついでに【偶数乗和】
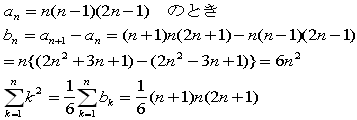
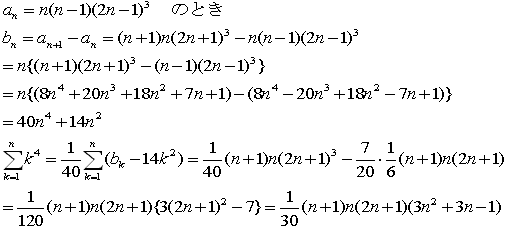
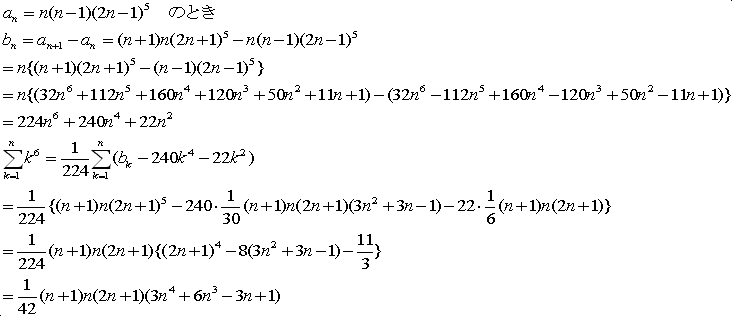
要点は、ａ1＝０で、ｂnをとったときｎの偶数乗が残るようにａをおけばよいわけです。
(1)
an={n(n-1)}2 とすると、an+1=(n+1)2n2 となり、
an+1-an=(n+1)2n2-n2(n-1)2
=n2{(n+1)2-(n-1)2}=4n3
bn=an+1-an なので、bn=4n3・・・答え
(2)
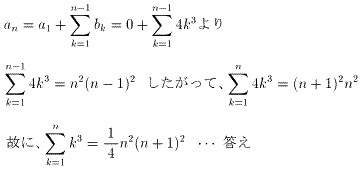
(3)
an={n(n-1)}3 とすると、an+1=(n+1)3n3 となり、
an+1-an=(n+1)3n3-n3(n-1)3
=n3{(n+1)3-(n-1)3}=n3(6n2+2)=6n5+2n3
bn=an+1-an なので、bn=6n5+2n3・・・答え
(4)
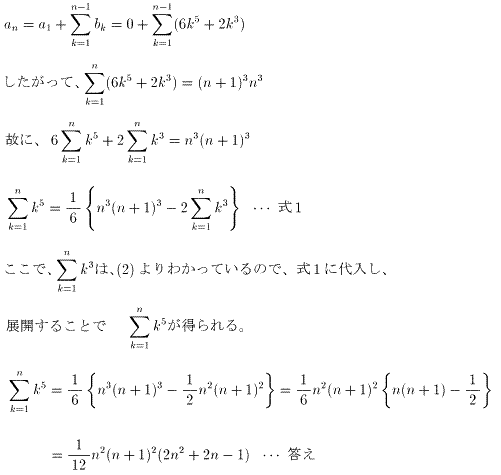
(5)
an={n(n-1)}4 とすると、an+1=(n+1)4n4 となり、
an+1-an=(n+1)4n4-n4(n-1)4
=n4{(n+1)4-(n-1)4}=n4(8n3+8n)=8n7+8n5
bn=an+1-an なので、bn=8n7+8n5・・・答え
(6)
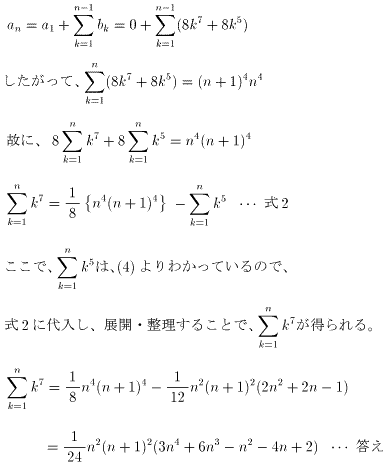
(7)
an={n(n-1)}5 とすると、an+1=(n+1)5n5 となり、
an+1-an=(n+1)5n5-n5(n-1)5
=n5{(n+1)5-(n-1)5}=n5(10n4+20n2+2)=10n9+20n7+2n5
bn=an+1-an なので、bn=10n9+20n7+2n5・・・答え
(8)
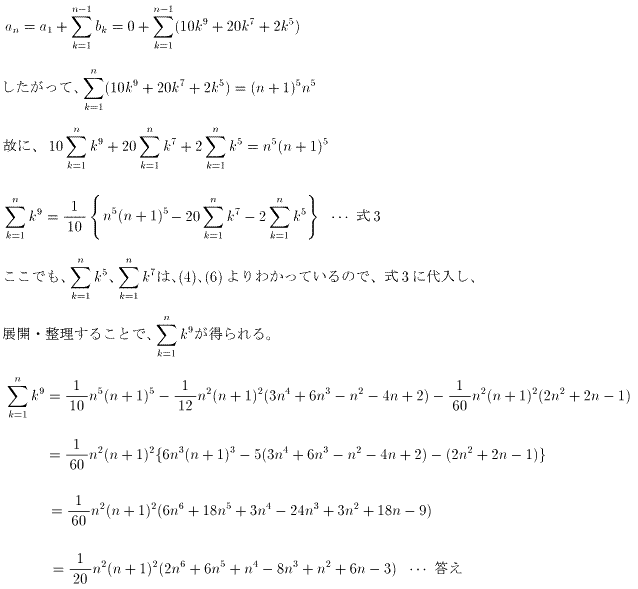
＜追記＞
私は、大学生のときに、パスカルの公式（式.4）と二項定理を使って、累乗和の公式を求めましたが、計算に何時間もかかりました。
この問題の奇数乗和の公式の求め方は速くていいですね。偶数乗和についても、同じようにして求められないか、
チャレンジしてみようと思います。
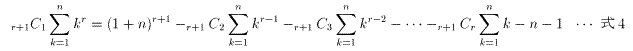
ちなみに、r=4,6,8のときは、それぞれ
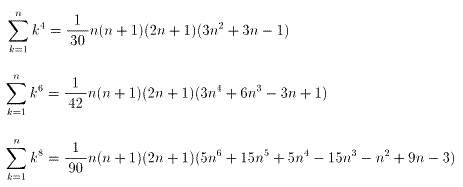
になります。
