Colloquium

NO.229
Weekend Mathematics／コロキウム室／NO.229

NO.1718　　　マクローリン展開　　2008.3.31　　水の流れ

第２０６回数学的な応募問題


皆さん、ある関数について、原点にあるいろいろな情報を読み取るだけでその関数を決定できることを ご存知ですか。その情報とは原点におけるｙ座標、第1次導関数の微分係数、第２次導関数の微分係数、 第３次導関数の微分係数、・・・、第ｎ次導関数の微分係数のことです。では問題です。



注：この記事に関する投稿の掲載は、２００８年４月２１日以降とします。

NO.1717　　 べータ関数(2)　　2008.3.31　　夜ふかしのつらいおじさん

先ず、次の式を示しておきます。つまり、Ｉ（m,n）＝I（n,m）で交換可能ということです。

　　　
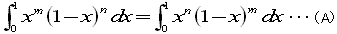
(A)の左辺で、1−ｘ＝ｔ とおくと 　　　ｘ＝1−ｔ
　　　ｘが 0→1 のとき、ｔは 1→0
　　　ｄｘ＝−ｄｔ
をふまえて

　　　
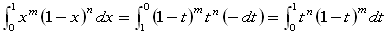
となるからです。
次に、A（m,n）を２通りで計算しておきます。

　　　
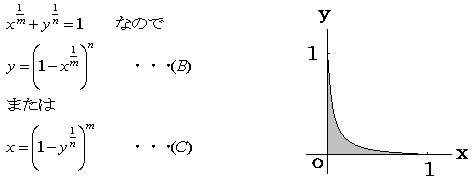
（B)の形をｘ軸方向に積分してみます。

　　　
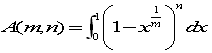
ここで、

　　　
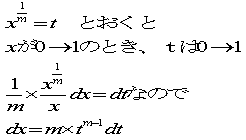
をふまえて

　　　
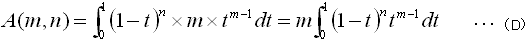
（C)の形をｙ軸方向に積分してみます。

　　　
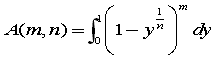
ここで、

　　　
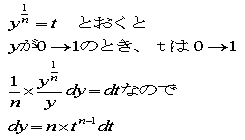
をふまえて

　　　
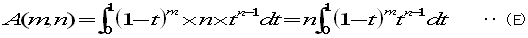
同じ部分の積分なので（D)と（E)とは同じ値です。 このことは、次の計算でも確認できます。

　　　

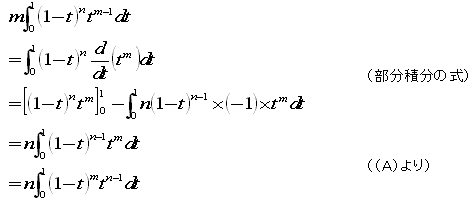
問１　

　　　

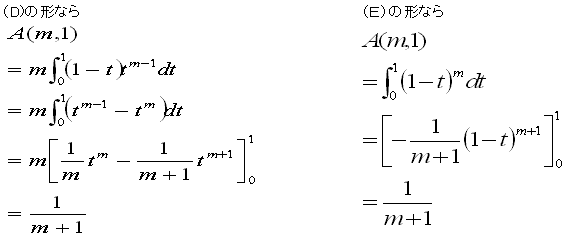
問２　A(m,n+1)を（E)の形で、A(m+1,n）を（D)の形で考えると

　　　

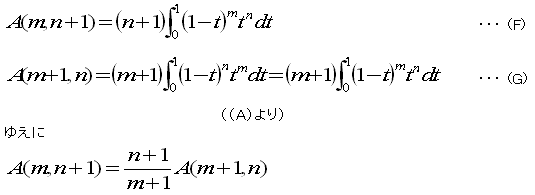
問３　

　　　

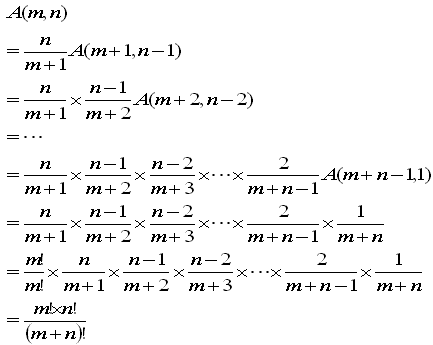
問４　

　　　

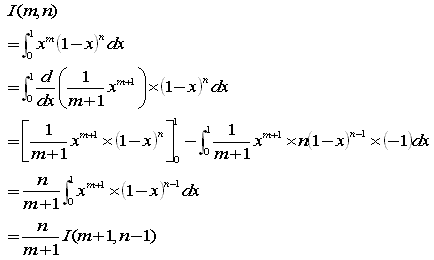
問５　

　　　
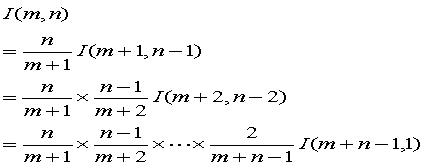
ここで、Ｉ（m+n-1,1）は

　　　
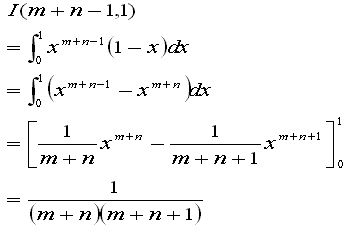
なので

　　　
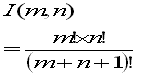
あるいは、A（m,n）の結果を使えば

　　　

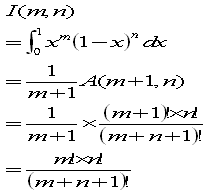
問６　

　　　
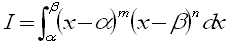
ここで、ｘ-α＝ｙとおくと
　　　ｘが α→β のとき、ｙは 0→β-α
　　　ｄｘ＝ｄｙ
をふまえて

　　　
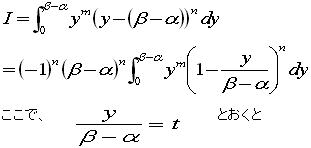
　　　ｙが0→β-αのとき、ｔは0→1
　　　ｄｙ＝（β-α）ｄｔ
をふまえて

　　　
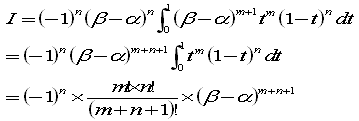
問６において、ｍ＝ｎ＝１とすると、

　　　

NO.1716　　　べータ関数　　2008.3.10　　水の流れ

第２０５回数学的な応募問題


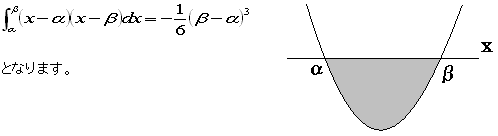
皆さん、過去の大学入試問題集（数研出版）を見ていると、べータ関数に関するものがあります。 そこで次の問題を紹介します。



注：この記事に関する投稿の掲載は、２００８年３月３１日以降とします。

NO.1715　　 正ｎ角形の３頂点(2)　　2008.3.10　　夜ふかしのつらいおじさん

問題３

（１）ｎ個の頂点のうちから３つを選んで結べば三角形になるので

　　　

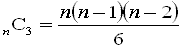
●ｎが奇数のとき

（２） 鈍角三角形の個数
「１」から「(ｎ+1)／２」の頂点から「１」を含んで、 ３個の頂点を結べば、鈍角三角形になります。 次に右にずらし 「２」から「(ｎ+3)／２」の頂点から「２」を含んで、 ３個の頂点を結べば、鈍角三角形になります。 このように右回りに順番にずらして数えます。 つまり

　　　
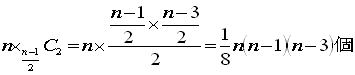
（３） 直角三角形の個数
ｎが奇数のときは、どの２点を結んでも直径になりません。 （直径にたつ円周角は９０°です） だから、０個です。

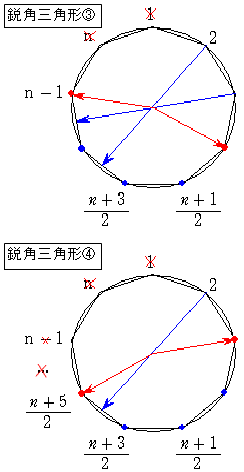
（４） 鋭角三角形の個数
(1)「１」を含むとき
「２」を含むなら、もう１個は「(ｎ+3)／２」の１個
「３」を含むなら、もう１個は「(ｎ+3)／２」か「(ｎ+5)／２」の２個
・・・
「(ｎ+1)／２」を含むなら、もう１個は「(ｎ+3)／２」から「ｎ」の(ｎ-1)／２個

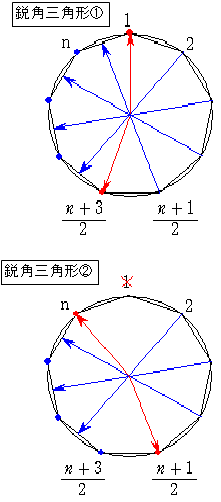
(2)「ｎ」を含むとき（「１」は含まない）
「２」を含むなら、もう１個は「(ｎ+1)／２」か「(ｎ+3)／２」の２個
「３」を含むなら、もう１個は「(ｎ+1)／２」から「(ｎ+5)／２」の３個
・・・
「(ｎ-1)／２」を含むなら、もう１個は「(ｎ+1)／２」から「ｎ-1」の(ｎ-1)／２個

(3)「ｎ-1」を含むとき（「１」、「ｎ」は含まない）
「２」を含むなら、もう１個は「(ｎ-1)／２」から「(ｎ+3)／２」の３個
「３」を含むなら、もう１個は「(ｎ-1)／２」から「(ｎ+5)／２」の４個
・・・
「(ｎ-3)／２」を含むなら、もう１個は「(ｎ-1)／２」から「ｎ-2」の(ｎ-1)／２個

(4) 「(ｎ+5)／２」を含むとき（「１」から左回りに「(ｎ+7)／２」は含まない）
「２」ともう１個は「3」から「(ｎ+3)／２」の(ｎ-1)／２個
(1)から(4)を全部合計すると

　　　

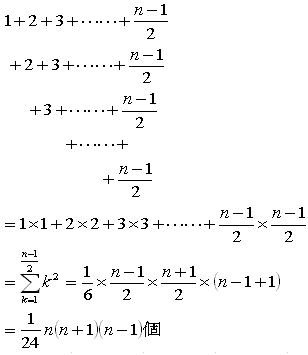
（２）から（４）を合計するともちろん（１）の結果になります。

　　　

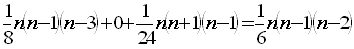
●ｎが偶数のとき

（２） 鈍角三角形の個数
「１」から「ｎ／２」の頂点から「１」を含んで、 ３個の頂点を結べば、鈍角三角形になります。 次に右にずらし 「２」から「(ｎ+2)／２」の頂点から「２」を含んで、 ３個の頂点を結べば、鈍角三角形になります。 このように右回りに順番にずらして数えます。 つまり

　　　

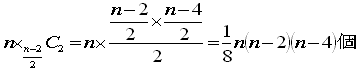
（３） 直角三角形の個数
ｎが偶数のときは、直径の両端となる２点と任意の点を選びます。 （直径にたつ円周角は９０°です）だから、

　　　

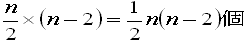
（４） 鋭角三角形の個数
ある点の両隣と中心に関して対称な点を含んでいると鋭角三角形を作りません。 下の図は「１」とその隣や中心に関して対称な点を用いて作った三角形です。


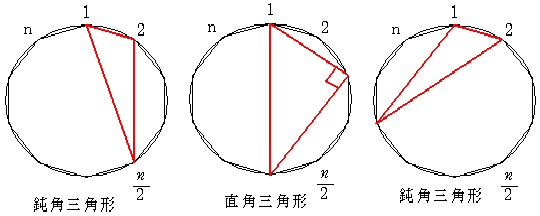
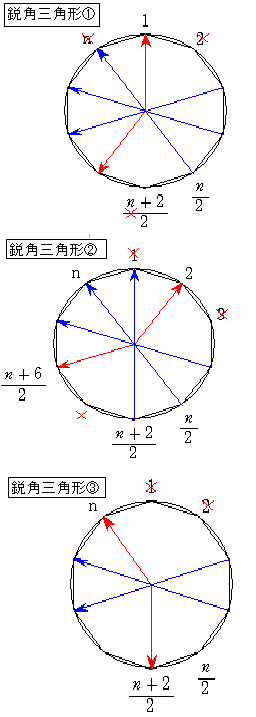
数えるときはその点を除きます。

(1)「１」を含むとき
「３」を含むなら、もう１個は「(ｎ+4)／２」の１個
「４」を含むなら、もう１個は「(ｎ+4)／２」か「(ｎ+6)／２」の２個
・・・
「ｎ／２」を含むなら、もう１個は「(ｎ+4)／２」から「ｎ-1」の(ｎ-4)／２個

(2)「２」を含むとき
「４」を含むなら、もう１個は「(ｎ+6)／２」の１個
「５」を含むなら、もう１個は「(ｎ+6)／２」から「(ｎ+8)／２」の２個
・・・
「(ｎ+2)／２」を含むなら、もう１個は「(ｎ+6)／２」から「ｎ」の(ｎ-4)／２個
(1)と(2)は同じ個数になります。

(3) 「１」と「２」を共に含まないとき
・「ｎ」を含むとして
　　「３」を含むなら、もう１個は「(ｎ+2)／２」か「(ｎ+4)／２」の２個
　　「４」を含むなら、もう１個は「(ｎ+2)／２」から「(ｎ+6)／２」の３個
　　・・・
　　「(ｎ-2)／２」を含むなら、もう１個は「(ｎ+2)／２」から「ｎ-2」の(ｎ-4)／２個
・「ｎ-1」を含むとして（「ｎ」は含まない）
　　「３」を含むなら、もう１個は「ｎ／２」から「(ｎ+4)／２」の３個
　　「４」を含むなら、もう１個は「ｎ／２」から「(ｎ+6)／２」の４個
　　・・・
　　「(ｎ-4)／２」を含むなら、もう１個は「ｎ／２」から「ｎ-3」の(ｎ-4)／２個
　　・・・・・
・「(ｎ+8)／２」を含むとき（「ｎ」から左回りに「(ｎ+10)／２」は含まない）
　　「３」ともう１個は「5」から「(ｎ+4)／２」の(ｎ-4)／２個

(1)から(3)を全部合計すると

　　　

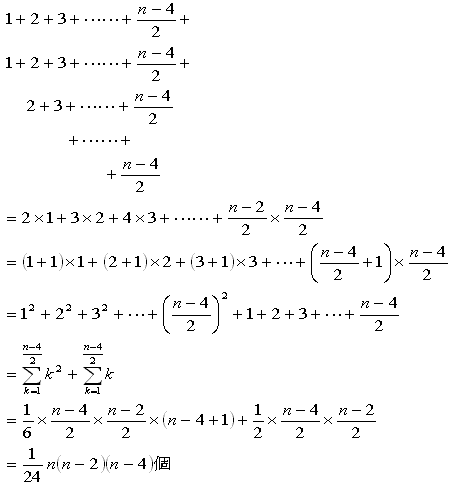
（２）から（４）を合計するともちろん（１）の結果になります。

　　　

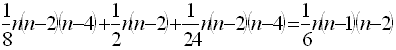
問題１ 上の式に代入して

問題２

　ｎ＝９ｎ＝10
(1)三角形の個数84120
(2)鈍角三角形の個数5460
(3)直角三角形の個数040
(4)鋭角三角形の個数3020

問題４
●ｎが奇数のとき

　　　
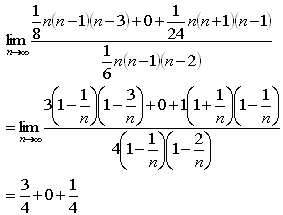
つまり、鈍角三角形の確率３／４、直角三角形の確率0、鋭角三角形の確率１／４です。

●ｎが偶数のとき

　　　
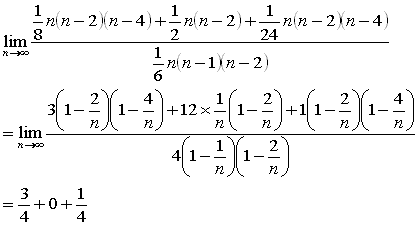
つまり、鈍角三角形の確率３／４、直角三角形の確率0、鋭角三角形の確率１／４です。

以上から、ｎの奇数、偶数によらず、鈍角三角形の確率３／４、直角三角形の確率0、鋭角三角形の確率１／４ となります。

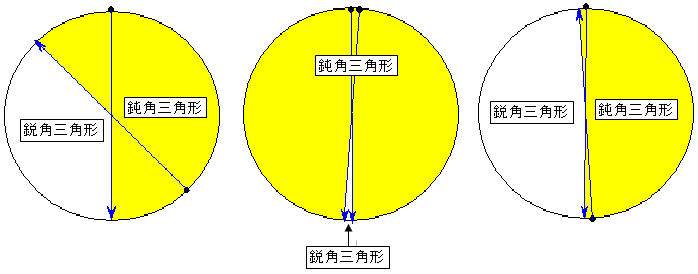
この結果は次のように考えると分かりやすいと思います。
左の図は、適当に２点をとり中心と対称な点と結んだものです。
黄色い部分の周上に第３の点をとりその３点を結べば鈍角三角形になります。
白い部分の周上に点を取れば鋭角三角形になります。

中の図は近くに２点をとったものです。
右の図は遠くに２点をとったものです。

第１の点はどこにとっても同じです。
第２の点は、第１の点から近くから遠くまでいろいろとることができますが、 真ん中あたりをとった場合、第３の点を取るときの確率が上の結果です。

　　　

NO.1714　　 ブルバキ 集合論１ 第１章 形式的な数学の記述のノート　　2008.3.1　　 ＤＤＴ

　初等的な古典形式論理学の良書ってないものだろうかと、ずいぶん思ってきた。
　例えば典型的に最も短い古典論理の入門書は、真理表から始まって、Bool演算あたりで終わっているのだが、 例えばＡ⇒Ｂ（ＡならばＢ）を「Ａでない、またはＢ」によって定義して良い理由が、 いま一つはっきりしない。さらに、全てを真理表で済ませてしまう態度が気に入らない。 プログラマーにとってはそれでも良いのだが、「意味は何処へ行った？」と言いたくなる。
逆に少し詳しい形式論理の入門書を読むと、確かに「自然推論」などが出てきて、 論理の公理系から出発して推論法則を導いていき、これなら全部読めばわかるかも知れないと期待させるのだが、 論理の公理系の意味は、結局は説明してくれない。 そして「数学基礎論を読め」と言わんばかりに、最後には手に負えなくなる。
それではと意味を訪ねて、例えばアリストテレスなどを間違って読んだとしよう （まぁ、クセジュ文庫あたりを想像して下さい）。三段論法が出てくる。

　　　「Ａ」を真，「ＡならばＢ」も真とする。このとき、「Ｂ」は真．

　確かに、これは意味もわかるし正しいと思えるのだが、本質的には、これだけで終わってしまう。 ∀xの話とか、∃xの話は、どこにもない。実際上これだけでは、 数学的な証明をするためには不足極まりない。
　なんか適当な本ってないのだろうか？。
　つまり真理表によらずに、論理の公理系から出発して初等論理を説明してくれて、 しかも数学基礎論なんて意識しなくて済む本である。なぜ公理系からの出発かというと、 真理表によらない導出は、推論規則の証明が付随するので、その証明過程で意味を考えられる、と思ったからである。
　ずいぶん昔だが、そのような事を思ったときに手に取ったのが、「ブルバキ数学原論 集合論１」だった。
　この本は、わずか200ページ余りである（ラッセルと比べてみて下さい）。 形式論理と関係する「形式的な数学の記述」はせいぜい100ページくらいで、残りは「集合論」だった。 しかも数学基礎論の話なんて一つも出て来ない。
　これって、すごく効率の良い本を手に入れたのではないだろうか？、と思えた。 そしてその序文には、こうも書いてあった。

　　　多少の抽象能力があれば、・・・この本は読める．
　　　・・・完全な公理的証明を一から付ける．

と・・・。違った。
　「完全な公理的証明を一から付ける」はその通りなのだが、世界中の識者の方々が、 「多少の抽象能力があれば・・・」というのは言いすぎだと認めていたのは、後で知った。 特にこれも世界中の識者の方々が認めていたように、 ブルバキの章末演習問題は専門領域をかなり意識して選ばれたものなので、 「多少の抽象能力があれば、・・・」程度のものではない。
　ブルバキを最初に手に取ってから、もう20数年の歳月が経ってしまった。 その間私は、ブルバキのわかりにくい記述に少しずつ慣れ、それとは別に、 DOS上の数値計算で始まったプログラマーとしての経歴のおかげで、今ではWindowsプログラマーを本職としている。 本職になって改めて思うのは、形式論理とプログラミング言語が良く似ているという事である。 考えてみればそれは当たり前の事で、プログラミング言語は、形式論理学を雛形として育って来た。
　しかしだとすれば、プログラミング言語の視点から形式論理を逆に読む事によって、その動機付け，構成， 証明方法などが、より明快に説明できる気がする。なんといっても、プログラミング言語は、 現実問題に適用され続けているので、良くも悪しくも具体的であり、形式論理よりわかりやすい。 そういうわけでこのノートを作ってみる事にした。ここでの立場は、形式論理（論理学）＝プログラミング という事になる。どちらも、アルゴリズムであるから。
　今までの経験からは、形式論理学（論理学）のわかりにくさは、一般的に言うと次の点にある。

  1. 論理学（形式論理学）は何も無いところから始める。よって、それ自身を展開するために、まずプログラミング言語を定義する。そうでないと何もできないからだが、だいたいが、この発想すら難しい。
  2. しかもプログラミング言語を定義しつつ、それまでの結果を利用してプログラムを行う（推論法則の証明）。通常は言語がありきでプログラムを行うので、この発想もまた非常に難しい。
  3. 推論法則の証明の中には、通常のプログラミングには入らないものまで含まれる（証明の方法の証明）。通常それらは、プログラミング言語パッケージの組み込み機能となり、意識する事はない。よって、それを行う動機が掴めない。
  4. 言語のある部分を定義した時、その部分のWell-Difined性（矛盾なく定義できる事）の証明をしてくれない。何かを定義した時には、原則Well-Difined性の証明は、数学では必須であるにも関わらず。
  5. それには理由があって、何も無いところから始めた以上、Well-Difined性の拠り所とする基盤が、数学になっていないからで、それは現実（実在論）を見るしかないからである。従って、定義の意味が語られない。しかし実在論（定義の意味）は是非欲しいところである。
  6. さらに初学者が混乱する理由として、上記の定義，証明などは、形式論理学の中で、まさに形式的に定義されるものなので、説明文の中では使えないし、みなやろうとしない。

　個人的な意見では、上記の1〜6が渾然一体となって記述され、初学者を非常に混乱させる。 このノートでは、上記に整理して応えようと思った。
　このノートは「ブルバキ 集合論１ 第１章 形式的な数学の記述のノート」であり、基本的には、 日本語訳された原文に従った章立てと番号を採用しているが、次の点は違う。

  1. 原文の「代入法則」の部分は「常識的にやればわかるだろう」という事で、いっさい割愛した。それは、ＣＦｎで表される「法則」である。ここでｎは、代入法則の番号。
  2. その他のＣｎで表される「法則」も、原文と必ずしも一致していない。必要に応じて、省略できると思えるものは省略し、番号を詰めている。
  3. 先ほど書いたが、ブルバキの章末問題は、本文の内容から言うと難しすぎるものが多い。これらも、一切扱っていない。

　ここまで書いてきたが、二つの問題がある。それは、なぜブルバキなのか？、という事と、 なぜ数学を形式化した記述で表す必要があるのか？、という二点である。一つ目についてはこうなる。
　「ブルバキ数学原論 集合論１ 第１章 形式的な数学の記述」は非常にコンパクトにまとまった形式論理学と思える。 しかも日本で出ているある本によれば、それは初等的範囲に属する事になる。 これには正直言ってびっくりしたが、たぶん「数学基礎論」の話を扱っていないからだし、 いまでは章末演習問題を除けば、そうかも知れないと思っている。 一時ブルバキの「数学基礎論」が出るかも知れないという噂が流れたそうだが、結局実現しなかった。 また最近（社会人のくせに）大学に通っていて思うのだが、プルバキのスタイルは、 50数余年の月日を経て、やっと大学初年級の教育現場に降りてきたと感じる。 いまさらプルバキを取り上げるのは、そのためである。
　二つ目についてはこうなる。数学上の実際問題として、「数学基礎論」を意識しないならば、 数学の形式化なんて不要だ、という意見には私も賛成である。しかしながら自分は、 数学の形式化は一つの価値を生み出すと思っている。これは現在の職業からそう思う。それについては、 「はじめに」に書いた。

はじめに
（なぜ数学を形式化するのか？）


　史上、最も普及した数学は、小数計算だと思う。 ここで言う小数計算とは、経理の計算などで用いられる10進位取り記法と、 それに付随する「掛け算九九」と「足し算九九」表の事である。 現在のような形に小数計算がまとめられたのは、300〜400年程前の事と言われている。 逆に言うと、たかが小数計算の普及のために、3〜4世紀もかけたわけだ。
　現在では「算数」と言われているが、10進位取り記法は本当は決してやさしくない。 それは高度に抽象化され形式化された数値表現システムである。10進位取り記法は立派な数学システムであり、 4世紀も前には、高等数学の一つだった。だからその普及には、400年も必要だったと言えるかも知れない。 誰もが考え出せることなら、そんな事にはならなかったはずだ。しかし近代以降になって、教育制度が整備されると、 爆発的に普及した。
　運用規則がやさしかったからだ。小数計算に必要な事は3つしかない。 まず数学（算数）の代表的な暗記物である「掛け算九九」表。それと無視されがちだが、 本当は「足し算九九」表も使っている。最後に、10進位取り記法の、「桁の繰上げ」と「10借りて来る事」である。
　これらの規則が何故やさしいかと言えば、おぼえるのにそんなに面倒でないことが最大の理由だ。 そして、その3つさえ記憶してしまえば、小数の意味すら知らなくても、必ず正しい答えを出せる。 しかも、いかなる場面にも、その運用規則は通用する。この運用規則は意味を知らなくても使えるので、 形式的なものだ。
　意味を知らなくても、考えなくても答が出る。ここが重要である。 その価値は、経理の計算は言うに及ばず、科学技術計算，現場技術者の仕事， コンピューターが用いる数値計算ライブラリーにまで及ぶ。
　コンピューターのCPUは何も考える事ができない。にも関わらず人間と同じように答えが出せるのは、 何も考えなくても正解に達するように、計算手続きが作られているからだ。それがプログラムというものだ。
　一般に手続きとはアルゴリズムであり、それはコンピュータプログラムと同じものだ。 そこでは代数計算のように、与えられた前提から一定の計算規則を踏めば、 論理的に正しい解答が必ず得られる事が保証される。そのような状況が、 普遍的に正しい形式的論理手続きの存在である。
　何故なら、一定の計算規則を踏めば必ず正解に達するとは、いったん前提が与えられた後では、 前提の意味内容を一切問題にしなくても良いという事である。 そうでなければ普遍手続きは前提の意味内容に左右され、 どのような場合にも適用できるような一般規則にはなり得ない。
　意味を考えなくても「答えを出せる」事は、形式化の価値なのだ。 それは絶対に間違いのない形式的な推論手続きといっても同じだ。 それが数学の形式化への動機付けになる（少なくとも一つの）。
　このような発想は近代以降のものではない。アリストテレスは、そもそも現在ある論理学の系譜の創始者であるし、 ライプニッツは普遍的な思考代数を夢想した。 ライプニッツの壮大な夢に比べれば卑小かもしれないが、 非常に現実的で有用な思考代数を提供して今に残っているのは、デカルトの解析幾何学である。 結局これは、グラスマンの線形代数へと受け継がれて行き現代に残っている。 そしてグラスマン自身も、数学の一般化と理論的整備を行う上で、普遍的形式的手続きを重視した人だと言える。
　近代以降になると、歯車式計算機の発想で、差分機関，解析機関が登場する。 計算は、「何も考えない機械」でも可能である事、それが「計算と形式的論理手続き」の本質であり 「価値」である事が、気づかれたのだ。
　そうして最後に、ゲーデル，チャーチ，チューリング達が現れる。最近ではチャイティンがいる。 これらの人々の最終的な結果は、「純粋に形式的で普遍的な一般手続きは存在しない」である。 最終的には、「意味」を考えなければ解けない問題も存在する。しかしだからと言って、 これらの人々は「可能な範囲で数学の形式化を行っても、その結果は無意味である」とは言っていない。
　昔から、絶対に間違いのない手続きを得る事は数学における一つの目標であり、 意味の関わらない構文論的証明を得る事は、いまでも数学の重要な仕事の一部だと思う。
　というわけで、推論の形式的で抽象的な雛形の研究は、古来から行われてきた。 そこでは多くの場合、次の7つの論理記号の運用を、代数学における移項の法則のように定めれば良いことが、 次第に明らかになっていった。

  1. 「否定」 （ここではこれを、〜で表す）．
  2. 「または」（ここではこれを、ouで表す）．
  3. 「ならば」（ここではこれを、⇒で表す）．
  4. 「かつ」 （ここではこれを、etで表す）．
  5. 「ある」 （ここではこれを、∃で表す）．
  6. 「任意」 （ここではこれを、∀で表す）．
  7. 「等しい」（ここではこれを、＝で表す）．

　これらの公理的な運用を定める事が、以下の第１章の主要な目的である。

　構文論的な証明が存在するかどうかは、その数学分野が流行るかどうかの決定打になる、 というのが自分の意見である（対立概念は意味論的証明だ）。 もちろん応用分野が見つかるという前提はあるのだが、見つかった時に、 その数学が普及するかどうかは、構文論的証明の有無に左右されると思う。 最たるものは、やっぱり銭計算である。

概 要


　以下ではプログラミング言語として、一般的に普及していると思われるVisual Basicを採用する。 他言語しか知らなくても、Visual Basicは「わかる」と期待する。何故なら「Basic」の構文は易しいから。
　「はじめに」で述べたように、ここでの立場は、広い意味での「形式論理＝プログラミング言語」である。 しかも一から言語作りを始める。言語を作るには、最初に「語彙」を定めなければならない。 「語彙＝基本単語の集まり」である。ここではそれを「形式論理＝プログラミング言語」を手掛かりとして行いたい。 よって最初に行うべき事は、形式論理の観点から、「Visual Basic」の基本語彙を確定する事だ。

［1］プログラミング言語の基本語彙
　現在の汎用プログラミング言語は、非常に巨大なLiblaryを抱えている。 Liblaryとは、「組み込み型」とか「組み込み関数」，「組み込み機能」とか言われるものである。 代表的な「組み込みなんとか」を揚げれば、以下となる。

  1. 汎用のRuntime Liblary（File入出力，四則演算，型変換関数，数学関数など）．
  2. 基本Class Liblary（整数，実数，複素数などの全ての数値型，OSとの相互作用で必要な全ての型）．
  3. 汎用Helper（OSの時刻を取得するとか、画像のWindow Handleを取得するとかのAPI機能）．

　これらは全てLiblaryであり、 「Visual Basic」の基本語彙ではないと言える。 何故ならこれらは、純粋なBasicやC言語を使って、「Visual Basic」と言われる「言語Package」に、 後から付加されたものだからである。四則演算（＋，−，×,／）も、全ての数学関数も（sin，cos，tanなど）、 実数や整数でさえ、Liblaryの一部であり、基本語彙ではないと考えられる。
　では、純粋なBasic言語とは何なのか？。公式には認められていないが、全てのプログラミング言語には、 純粋な言語リファレンスとでもいうべき部分が、必ず存在する。 その部分に限っては、どんな言語に関しても厳密に同じである。 理由は、CPUの基本機能だけでやれる事を記述しているからだ。 プログラミング言語が、形式論理学を雛形として発展してきたように、 CPUとは、形式論理学の基本機能を物理的に実現したものだと言える。 つまり、ある言語の基本語彙を知りたいなら、CPUの基本機能に関わる部分を調べれば良い。 そこには、次の五つの機能しかない。

(1)逐次実行とLoop．
(2)四則演算．
(3)二値判断．
(4)型定義．
(5)型宣言．
　順番にやろう。

(1) 逐次実行とLoop．
　逐次実行とは、書かれたプログラムを上から順番に読んで実行するという、 CPUの基本機能である。通常は言葉にすらされないが、 これがプログラムという手続きの基本要件である。ここから言える事は、 形式論理も逐次実行だという事である。つまり「まだ証明されてないものは、使用不可」と言い換えても良い。 これは、形式論理の暗黙の基本仕様の実現である。 Loopとは、繰り返される同じ手続きを、省略して書く方法だ。 従ってLoopは常に逐次実行に置き換えられる。

(2) 四則演算．
　さっきも言ったように、四則演算と全ての数値型は、本当はLiblaryである。しかしながらCPUとは、基本的に加算回路なのである。 そして加算を除く四則演算は加算回路から構成でき、四則演算を実現する電気回路が、 今ではCPU自体に内蔵されている事がほとんどだ。そのような事情から、 四則演算も「純粋な言語リファレンス」に通常は入って来る。
　加算機能がCPUの基本機能になったのは、現在の技術事情では、CPUを加算回路で構成するのが、 最も効率的であるという物理的理由に他ならない。未来のCPUは、加算回路に基づかないかも知れない。 その時には、加算も含めた四則演算は本当のSoft Ware Liblaryになっているだろう。 原理的な話として四則演算は、二変数の組み込み関数である。 現在の状況で言うと、そのプログラムは、たまたまハードウェアで実装されているだけだ。 従って、ここでの立場では、それらを基本語彙として認めない。

(3) 二値判断．
　まずCPUの基本機能に二値判断がある、という事は重要だ。標準的な形式論理学は、真か偽か、 二つの状態しか関係に対して認めない。これなどは、プログラミング言語が、 形式論理の標準理論をもとに発展してきた事の証左である （真偽以外の状態もあり得る論理は、様相理論と言われる）。
　典型的なIfブロックは、以下のようになる。

If (x = 1) OR (x = 2) then
y = 3
Else
y = 4
End If

　意味はわかって頂けると思うのだが、ここには形式論理における、5つの基本語彙が現れている。
　一つは対象式「x，y」であり、もう一つは関係式「x = 1，x = 2」で、三つ目は特殊記号「=」、 そして論理記号「OR」、最後に「y = 3，y = 4」は存在の限定作用素「∃」を導入する。
　当たり前なのだが、「一つの文字は対象を表す」という暗黙の規則は、 形式論理もプログラミング言語も同じである。もっともプログラミング言語では、 「xy = 5」なども許される。二つ以上の文字で表される対象式については、(5)で述べる。
　(x = 1) と (x = 2)は関係式である。何故ならこれらは、If節の中で、True（真） またはFalse（偽）を返す関数だからだ。ここで「関数は基本語彙ではない」という意見と、 「関数は対象式だ」という意見には、素直にその通りだと言う。
　ただしこれらは、CPUという物理設計に基づいた仕様でそうだというに過ぎない事を、注意する。 形式論理の立場では、TrueまたはFalseを返す関数こそが、関係式という関係である。それによって真理表を作る。
　コンピュータにおいて関係式が関数になっているのは、CPUが値そのものしか評価しないからだ。 なので(x = 1) や (x = 2)は、TrueやFalseという値を返す関数として実装される。 しかし論理上、TrueとFalseは、(x = 1) や (x = 2)が取りうる状態である。関数や対象ではない。 というか関数や対象とみなす必要がないのだ。それらの言葉は、もっと大事に扱われる。 従って確かに微妙だが、これらは論理上、ふつうは対象ではなく関係とみなされる。
　「=」は重み2の特殊記号と言われ、2項関係を表す。 特殊という言うからには、何らかの一般的ではない意味合いを含むのだが、 等号関係が現れないような数学理論というのは、ちょっと考えにくい。 それでも「=」を特殊記号とすれば、形式論理の一般的展開を想像できる。
　最初に「=」を含まぬような一般論を展開し、その後に「等号を持つ理論」の公理を導入して、 等号付理論を展開する、という手順である。とは言うものの、等号は非常に基本的な関係なので、 ブルバキの「形式的な数学の記述」の中に、「等号を持つ理論」は含まれている。
　「OR」は論理演算子である。「+」は加算演算子であった。このように演算子は、 つねに二変数の組み込み関数として実現される。「OR」の返り値は、TrueまたはFalseなので、 (Ａ OR Ｂ)も関係式とみなせる。他の論理演算子「AND」「XOR（排他的論理和）」などは、 全て「OR」と否定「Not」で書くことが出来る。従って基本「論理記号」として、「OR」と「Not」が必要になる。
　最後にIfブロック内にある(y = 3)と(y = 4)である。これらは関係式ではない。 かといって対象式でもない。 これらは純粋に、物理的なCPUの機能を表し、代入操作もしくは、メモリの領域確保と言われる行為である。 実際これらは、TrueもFalseも返さないから関数でもない。これらについての解釈も、(5)で述べる。

(4) 型定義．
　Object指向をやらない限り余り意識しないが、型定義とは言葉通り、 術後定義に他ならない。形式論理では、定義は既存の対象式や関係式を基にして行われるが、 プログラミング言語においては、ふつうは既存の対象だけが定義の基になり得る。 そこでの既存の対象とは、Libralyに存在する既存の数値型などである。例えばVisual Basicにおいては、 Singleという、単精度浮動小数点実数型がある。単純に考えれば、Singleは実数全体Ｒと同じである。 ただし有効範囲は-10300〜10300くらいで、有効数字は8桁である（コンピュータのメモリは有限ですから）。 型定義によって、次のようなPosition_Vector（位置ベクトル）構造体を作成できる。

Public Structure Position_Vector
Public x as Single
Public y as Single

Public Sub New(Byval x as Single，Byval y as Single)
Me.x = x
Me.y = y
End Sub

End Structure

　上記は通常の位置ベクトル(x，y)と同様に扱える。さらにベクトル間の演算も定義できる。

Public Shared OverLoades Operator + (Byval V1 as Position_Vector, _
                                     Byval V2 as Position_Vector) as Position_Vector
Dim V3 as New Position_Nector
V3.x = V1.x + V2.x
V3.y = V1.y + V2.y

Return V3
End Operator

　これらの詳細はどうでも良い。言いたいのは、 Position_Vector型の変数V1＝(x1，y1)とV2＝(x2，y2)があった時に、

Dim V1 = New Position_Vector(x1，y1)
Dim V2 = New Position_Vector(x2，y2)
Dim V3 = V1 + V2

と書くだけで、

V3 = (x1，y1) + (x2，y2) = (x1 + x2，y1 + y2)

が実現されてしまうという事実である。定義の目的は、この便利さであり、定義とは、 既存のものを組み合わせて新たな名前を付けたものに過ぎない。
　形式論理では（ブルバキだけかも知れないが） 「定義とは、事前定義された記号列の組み合わせに対する省略記法である」となっている。 プログラムミング言語においても型定義とは、既存の型を組み合わせた型を表す省略記法なのである。 V3 = V1 + V2を、型定義を使わずに実装したら、倍以上のコードを書かねばならない。

(5) 型宣言．

　型宣言とは、対象式の記述方法である。例えば、

Dim xy as Single

とは、xyは対象式（記号列「xy」は変数で、型は単精度実数型）という意味である。コンパイラーが、 どのようにして記号列「xy」を対象式とみなすのかは、驚くほど簡単な規則に従っている。
　コンパイラーは、Dim句とas句の間の記号列は、みな対象式（変数など）であると判断する。実際、

Dimxy as Single

などとすると文法Errorになる。つまりコンパイラーは、個々の単語（talkenと言う）を見分けるために、 半角または全角spaceを分離子（Delemeterと言う）として使っているという事だ。 Delemeterとしての半角，全角spaceはいくつあっても良い。

Dim   xy as Single（半角space三つ）

や、

Dim　　xy as Single（全角space二つ）

は文法Errorにならない。要するに、文字列「Dim」と「as」を読み取れれば良いのだ。
　ここで言いたい事は、二つ以上の文字で表される対象式を確定するためには、 何らかの目印が必要だという事である。Visual Basicの場合、それはDim句とas句である。 ブルバキでは、二つ以上の文字で表される対象式を確定するために、τ 記号が使われる。

τxy

は対象式といった具合だ。つまり、τで始まる記号列は、みな対象式だとみなす。そうでない文字列が、 関係式となる。τ記号自体は、論理記号とみなされる。
　よって形式論理において、組み込み型は二つしかない。
　　　対象式と関係式
がそれである。
　型宣言に関係しては、もう一つ重要な事がある。型宣言は、それだけを単独で用いても無意味である。何故なら、

Dim xy as Single

と言っただけでは、xyという対象式を決めただけで、その「値」は決めていないからだ。 原理的に言うとプログラミングの世界では、値を与えていない対象は、みな「空な対象」とみなされて、 値を与えていないxyの値を取得しようものなら、

Dim TestValue as Single = xy

などは実行時Errorになってしかるべきものである。 しかし数値である実数型（Single）などでは、それでは余りに不便なので、 宣言と同時に初期化がかかる。初期化とは、ある型のDefault値を代入する事である。 数値であれば、それは普通0だ。

Dim xy as Single（ = 0　が、コンパイル時に自動で付加される）

　これによって、Dim TestValue as Single = xyも実行時Errorにならず、めでたくTestValue = 0となる。 従って正直にやろうとすれば、

Dim xy as Single
xy = 1

とかしなければならない。ここで「xy = 1」は代入操作である。
　(3)で述べたが、代入操作とは、物理的なCPUの機能そのものを表し、関数でも関係でも対象でもないものだった。 機能とは、メモリの領域確保である。じつはこの機能は、次の一連の記述と同じと考えられる。 Ｒを実数全体とする。
　　　xy∈Ｒとする． （xyは実数だとする）
　　　(∃xy)(xy - 1 = 0)．（xy−1＝0を満たす、xyが存在する）
　まず「xy∈Ｒとする」が、「Dim xy as Single」に対応している。次に「xy - 1 = 0」を満たす「xy」 が存在する事は、どのようにして「証明」するのだろうか？。 答えは簡単で、「xy - 1 = 0」を満たす「xy」を「計算してみせる」のである。 その結果「xy = 1」となる。もう少し複雑な状況を考えてみる。
　　　xy∈Ｒとする．
　　　(∃xy)(xy2 - 2xy + 1 = 0)．
　同じように計算する。


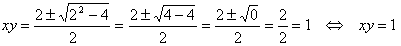
　何を言いたいかというと、これらはみな、
　　　xy∈Ｒとする．
　　　(∃xy)(xy = 1)．
と同じだ言いたいだけだ。プログラミング言語において、何かの存在証明を行うときには必ず、 その値が計算できる事を「してみせる」。それがプログラミング言語における存在証明になる。 「xy = 1」とは、その最も簡単な形である。もし、

Dim xy as Single
xy = "aaaa"

としたら、上記は文法Errorになる（実行時Errorですらない）。文字列"aaaa"は、実数ではないからだ。
　「xy = 1」のような時に限って（(∃xy)(xy = 1)がTrueである時に限って）、xy = 1 という代入操作は成功する。 このときメモリ上に、数値「1」を表すBit列が生成され（メモリの領域確保）、xyで表される数値は、 物理的に存在する事になる。まさに、(∃xy)(xy = 1)である。
　よって代入操作「xy = 1」は、「∃」の導入と同じであるが、形式論理では「∃」とペアになって、 「∀」も現れる。論理上(∀x)Ｒは、〜(∃x)(〜Ｒ)と同じだとされる。ここで、Ｒは関係式（xに関する条件） ，「〜」は関係式「Ｒ」や「(∃x)Ｒ」の否定「Not」を表すものとする。
　すなわち「全ての(任意の)xで、Ｒ(x)が成り立つ」とは、「〜Ｒ(x)を満たす対象xが存在しない」の と同じだと考える。プログラム上の「∀」の扱いは、結局「∃」の扱いと同じである。
　つうじょうは行わないが、どんなxに対しても〜Ｒ(x)がFalseになる事を確認するか（計算してみて）、 逆に、可能な全てのxに対して、Ｒ(x)がTrueになる事を確認する（計算してみて）。 結局「∀」は「∃」から導ける事になり、これは形式論理の考えといっしょである。 そして「∃」と「∀」は、もちろん論理記号である。
　以上、CPUの基本機能からは、次の4種類の基本語彙を取り出せた。 （）内は、プログラミング言語における呼称。

(1) 論理記号 ： τ，OR，Not，∃，∀．（予約語）
(2) 文字 ： 任意に導入して良い．特に一つの文字は対象を表し、対象式である．（変数）
(3) 特殊記号 ： 「＝」など．（演算子で予約語）
(4) 関係式と対象式 ：一つの文字かτで始まる文字列は対象式で、そうでないのは関係式．（型）

［2］文法（構成手続き）
　語彙（talken）の次に来るのは文法である。プログラミング言語において、 それはコンパイラー（Compiler）が担う。
　ここで注意すべきは、語彙（単語）の数は有限だという事実である。 にも関わらず我々は、無限の寿命さえあれば、無限に違った文章を喋る事ができる。
　まず文字（一文字の記号）は、英語であれば26文字であり、日本語でも漢字も入れれば数万だろうが、 とにかく有限である。しかし、単体の文字，文字から出来る記号，記号を集めた記号列， 記号列の列，・・・と、文章はいくらでも増殖させられる。
　という事は、文章の集りである言語とは、必然的に再帰操作を伴う。 有限の初期値から、無限を発生させる機構は再帰操作である。 例えば、z，x1，x2，・・・をプログラミング言語における数値型と事前に宣言された （初期化も含めた）変数とした時、 

z = x1 + x2 + x3 + x4

などは、典型的な再帰操作と言える。さっき言ったが、加算演算子は二変数の組み込み関数だった。 よって、上記において実際にされている事は、

z = (((x1 + x2) + x3) + x4

である。上記の簡単な規則が、いくらでも続けられるのは明らかだろう。 上記を形式論理風に言うと、少々もってまわった言い方になるが、 次のような「構成手続き」を認めた事になる。ここで関数とは、対象式だった。
　　　記号列Ａより前に対象式ＢとＣがあり、ＡがＢ＋Ｃであるとき、Ａは対象式．

「構成手続き」とは、単語の羅列と、意味のある文章を区別する規則であると言える。それが文法だ。 そして上記「構成手続き」は、z = (((x1 + x2) + x3) + x4の場合のように、再帰的に適用できる。
　実際に書かれた文章が、許容できる再帰規則を満たすかどうかを判定するのが、コンパイラーの役目である。　 再帰規則の中には、再帰しない規則も当然含まれる（一回だけの再帰と考える）。 xyが数値型と定義されたのにxy = "aaaa"などと代入を受けた場合は、一回だけの再帰規則に関するルールを適用して、Errorを出す。
　しかしコンパイラーの主目的は、いくらでも繰り返せる再帰規則に従っているかどうかのCheckであり、 Checkは「構成手続き（文法）」に従って行われる。
　というわけで言語は、「語彙（単語）」と「構成手続き（文法）」から出来ている（当たり前だが）。

［3］形式論理というプログラムの目的
　今までの事は、もちろん形式論理の枠内に収まる事ではあるのだが、じつは現時点では、 全然プログラムを書いていないのである。例えば「Visual Basic」という言語Packageを考えたとき、 その言語リファレンスを理解する部分と、理解したリファレンスに従って、 所定の目的を果たすプログラムを書く作業とがあるが、「Visual Basic」と言ったときには、 その両方が当然のように含まれる。同様に「形式論理学」と言ったときにも、その両方が想定される。 今までやって来た事は、言語リファレンスの理解の部分である。
　プログラムは、所定の目的に沿って書かれる。目的とは「解くべき問題」と言い換えても良い。 「解くべき問題」がなければ、プログラムを書く必要も無い。「プログラムの目的」という観点で、 形式論理と実用的なプログラムを比較したとき、形式論理は、 非常に特殊な目的を持ったプログラムである事がわかる。
　通常の実用的プログラムでは、問題の領域は限定されている。 極端に言えば、通常のプログラムで、「解くべき問題」は一個だ。

'a * x2 + b * x + c = 0 を解くプログラム
Public Sub Main()

'以下でDoubleは倍精度浮動小数点実数型を指示する。
範囲は-10300〜10300くらいで有効数字は16桁
Dim a as Double = 1
Dim b as Double = 2
Dim c as Double = 3

Dim x1 as Double
Dim x2 as Double
Dim D as Double

D = b^2 - 4 * a * c　'判別式

If D < 0 Then
　'「実数解なし」と表示する
Else
　x1 = 1/2/a * (-b - Sqr(D))　'Sqr()は√を表す
　x2 = 1/2/a * (-b + Sqr(D))　'Sqr()は√を表す
　'「実数解x1とx2」を表示する
End If

End Sub

は典型的な例だ。このプログラムは、ax2＋bx＋c＝0を解くために書かれており、 解くべき条件は一個しかない。解くべき条件が数千個や数万個あったところで、 このようなプログラムの集まりに過ぎない事は、明らかだろう。さらに言えば、 上記の出力x1，x2は「対象式」である。
　実用的プログラムの目的は、ある条件を満たす対象式を全て尽くす事だと言える。 実用的に求められる結果はつねに、「値（典型的には数値）」なのだ。でなければ、以後に使用できないから。
　これに対して形式論理学で書くべきプログラムは、正しい（真な）関係式を尽くすようなものである。 典型的例は、
　　　Ａ⇒Ａ
といったものであり、典型的に正しくない（偽な）例は、
　　　(〜Ａ) AND Ａ
などである。これらはどちらも恒真関係と言われるもので、条件（関係式）Ａが対象式xを含んでいたとしても、 Ａ(x)⇒Ａ(x) や (〜Ａ(x)) AND Ａ(x) は、xに関わりなく、常に真または偽になる。
　実用プログラムのレベルで考えると、このような特殊用途を持つプログラムが必要な時は、 特殊用途に相応しい組み込み関数があってしかるべきだ、という事になる。 この場合は、関数の「引数」として任意の関係式を取り、真な関係式を必ず返すような、 組み込み関数である。ただし形式論理において、「関数」という術語は非常に大事に扱われるので、 これは実用レベルで考えた場合の実装である。
　形式論理において、そのような組み込み関数に相当するものは、シェーマと言われる。 シェーマとは、次のようなものだ。

1゜理論Ｔの最初に現れる、一つ以上の関係式を、Ｔの明示公理と呼ぶ。明示公理に現れる文字を、 Ｔにおける定数という．
2゜Ｔのシェーマとは、次のような特性を持つ．
　a) シェーマの一つＳを適用して得られる結果は、Ｔの関係式である．
　b) ＴがＴの対象式、xを文字とする。ＲがシェーマＳの適用によって得られるＴの関係式ならば、 (Ｔ|x)ＲもＳの適用により得られる。
3゜Ｔのシェーマによって得られる全ての関係式を、Ｔの非明示公理と呼ぶ．

　上記において、理論Ｔとは、［1］で述べた「基本語彙」に、［2］で述べた「構成手続き」を再帰的に適用する などして得られる、具体的な記号列の列の事を指す。「はじめに（なぜ数学を形式化するのか？）」で述べたように、 形式的な数学の記述（形式論理）は、理論の意味内容に関わらないから、理論Ｔといっても、 「構成手続き」などによって発生し、具体的に書かれたところの記号列の列、以外の何者でもない。
　とにかく理論Ｔが一つあれば、その出発点として、理論の前提となる条件（明示公理と呼ぶ事にする関係式） があるはずだ、という話である（ない場合もあり得る）。 そして、その理論の前提である最初の関係式の中に含まれる文字（対象式）を、理論の定数と呼ぼうという わけだ（妥当な定式化と思える）。
　次にシェーマを使用した結果は、常に関係式Ｒで（関係式を返す関数で）、Ｒが文字x（対象式）を含んでいるとき、 xを別の対象式Ｔに置き換えた(Ｔ|x)Ｒも、やはりシェーマの適用によって得られなければならないと言っている。 これによってシェーマの適用結果が常に、恒真に成り得る事が保証される（恒真関係の真偽は、対象に関わらない）。 これは、シェーマという組み込み関数の、仕様定義である。
　具体的なシェーマの例を与える。次に述べるものは、論理的な理論（命題理論）のシェーマである （ouは、ORを表している）。

S1 (ＡouＡ)⇒Ａは、Ｔの公理．
S2 Ａ⇒(ＡouＢ)は、Ｔの公理．
S3 (ＡouＢ)⇒(ＢouＡ)は、Ｔの公理．
S4 (Ａ⇒Ｂ)⇒((ＣouＡ)⇒(ＣouＢ))は、Ｔの公理．

　例えばS1を関数として見た場合、その引数は関係式Ａで、返り値は(ＡouＡ)⇒Ａという関係式である。 S2とS3は、引数(Ａ，Ｂ)を取り、S4は(Ａ，Ｂ，Ｃ)を取って、返り値はやはり関係式である。 S1〜S4が明らかな恒真関係である事はすぐわかるだろう。 引数Ａ，Ｂ，Ｃには、「基本語彙」と「構成手続き」によって得られるどんな関係式も、 明示公理，非明示公理なども任意に代入して良い。
　面倒なのは、たとえ関係式Ｒがシェーマの適用結果であったとしても、まだＲは真だとは認められていない、 という事である。形式論理は意味内容と関わらないので、そこにはもともと、真とか偽とかの概念はないのである。 「真とか偽」とかは「意味」だからだ。
　形式論理は構文論的なので（意味論的ではいけないので）、何かの関係式を「意味として真」だと認めるにしても、 「認証手続きを具体的に、手順として記述する」必要がある。 それが「ある関係式が、定理になるか否かを判別する手順」である。 これは、ax2＋bx＋c＝0を解くプログラムにおいて、判別式Dを使って出力を選択しているようなものだ。 形式論理における出力が、「証明の全文」である。

理論Ｔにおける証明の全文とは、次のものからなる．
1゜必要な関係式や対象式に関する補助的な構成手続き．
2゜証明．すなわち、Ｒを関係式として、次のいずれかの条件を満たす記号列があること．
　　a) ＲはＴの明示公理．
　　b) ＲはＴのシェーマから得られる．
　　c) Ｒより前に、関係式ＳとＳ⇒Ｒがある．
3゜Ｔにおける定理とは、Ｔの証明の中に現れる関係式のこと．

　そして結局は、定理は理論における真な関係と、「呼ばれるもの」になるのだが、 ある関係式が意味として真だと認証するためには、上記「認証手続き」を使わなければならない。
　上記a)，b)によって、明示公理と非明示公理（シェーマの適用結果）が恒真である事がやっと保証される。 C)は「三段論法」と言われる認証手続きである。 よって形式論理は、理論の公理，自明な恒真関係（シェーマ）および「三段論法」だけから、 定理（真な関係）を導いていく手順だと言える。

［4］混成言語プログラミング
　異種言語でプログラムを作る事を、混成言語プログラミングという。次の簡単なプログラムを考える。

'1〜10を足すプログラム
Public Sub Main()
Dim StartN as Integer = 1
Dim EndN as Integer = 10
Dim Total as Intger = 0
Added(StartN，EndN，Total)
' Totalを表示する
End Sub


Private Sub Added(ByRef StartN as Integer，ByRef EndN as Integer，ByRef Total as Integer)

For i as Integer = StartN to EndN
Total = Total + i
Next i

End Sub

　1〜10を足すプログラムは、Sub Routine「Added」を使っている。 Addedは整数型の引数(StartN，EndN，Total)を取る。いまAddedはBasicで書かれているが、 必ずしもそうしなくて良い。例えばFortranを使い（Windows対応のFortranってあるんですよね）、

Subroutine Added(StartN，EndN，Total)
Integer*4 StartN
Integer*4 EndN
Integer*4 Total
Integer*4 i

Do i = StartN，EndN
Total = Total + i
End Do

End Subroutine

をMain RoutineにSub Routineとして与えても良い。 もちろんSubroutine Addedを使うためには、コンパイラーにそれなりの指示を出さないといけないが、 それは枝葉末節な事だ。Fortranで書かれたSub Routineも「使える」という事が重要である。
　このような事が可能なのは、汎用プログラミング言語は、そのLiblaryを除けば、 どれも本当に厳密に同じだからだ。じっさいPrivate Sub AddedとSubroutine Addedが全く同じものである事は、 かなり明らかだろう。書き方が違っているだけである。
　もっと原理的な話として、Basicで書かれた、次のような「別の」Sub Routineも使用可能だ。

Private Sub Added(ByRef S as Integer，ByRef E as Integer，ByRef T as Integer)

For k as Integer = S to E
T = T + k
Next k

End Sub

　引数(StartN，EndN，Total)を取るPrivate Sub Addedと、引数(S，E，T)を取るPrivate Sub Addedとが、 全く同じものであるのは、さらに明瞭だろう。 変わらないのは、「For」とか「+」とかの「予約語」だけである。 これらは形式論理の「論理記号」に相当する。それらさえ一致すれば、個々の変数名がどうあろうと、 成される事は一緒である。これこそが、意味内容に関わらない形式言語一般の特徴である。 そこで重要なのは、結局「単語の並び方」だけなのだ。そのように考えれば、Subroutine Addedが使える事も、 その一般化に過ぎない。
　以上と実質的に同じ事が、後述する「理論における代入」において行われる。 「理論における代入」などと言うと、何か大掛かりなものに聞こえるが、本質はこれだけである。

［5］Application構造（Sub Routine，Function，Local変数）
　定義は多少あいまいだが、単純かつ具体的な目的を実現するプログラムを集めて、 より抽象的で人間的な欲求を実現するプログラムを、一般にApplicationと呼ぶ。経理ソフトなどがその典型だろう。
　経理ソフトの個々の機能は、金という数値を足したり、経費／原価を行って原価率を出したりする 単純かつ具体的なものであるが、ソフト全体では、経理という抽象的システムを実現する事が目的だ。
　それは単なる数値では表す事が出来ず、数値全体の集合を定性的に眺めて、初めて意味を了解できる。 しかし、それだけの意味合いの違った数値を計算するためには、 それぞれの数値を計算する個別プログラムもたくさん必要になる。
　大規模Applicationでは、個別プログラムは数千〜数万にもなる。 さっきの「1〜10を足すプログラム」ではSub Routine Addedを一個使ったが、 もちろんAdded(StartN，EndN，Total)の部分を、Private Sub Addedの中身で置き換えて、 Sub Routineなしにしてもいいのだ。
　問題はSub Routineを使わないとすると、大規模Applicationでは、Private Sub Addedの中身に 相当するコードで、Main Routineが数十万行にもなってしまう事だ。 これではApplicationのDebugや保守はほとんど不可能になる（個人的には2万行までやった事がある）。
　しかしMain Routineが数十万行になったところで、上から順番に読んで行くだけなのだから、 Sub Routineを用いない書き方のほうが、より直線的・直感的で、検査しやすいのではないだろうか？。
　一理ある。上記意見が妥当な場合も、確かに存在する。しかし一般的には、 Sub Routineを使わない代償の方が大きい。最初に述べておくべき事は、現在のプログラマーは、 文法Errorからは、ほぼ完璧に開放されているという事実である。
　現在のコンパイラーの文法違反Checkは、信じられないくらい良く出来ている。 プログラムをコンパイルにかけた時、文法Errorがあれば、それらはまとまった見やすい形で一覧表示される。 文法Errorリストの一つをClickしたら、その行に跳べるだけではなくて （これだけでも昔は、驚異の機能だった）、今ではその箇所のコードの修正候補リストまで表示してくれる。 修正候補リストの一つをClickすると、自前で書いたコードを、その通りに修正してくれる。 今やプログラマーは、文法Errorからは完全に解放されていると言って良い。 従って残る問題は、文法Errorは出さないが、結果は現実に合わないという、間違いの発見である。 そのような「間違い」を、総称してバグと言う。「Bug」と書き、「虫」という意味だ。
　その多くは「 + と - を取り違えた」とかいうケアレスミスから生じる。 よって個々の計算式や文は、文法的には正しく、「意味を考えない」コンパイラーには発見しようが無い。 これは厄介である。しかも一般的な傾向として（個人的意見では）、
　　あるApplication開発に関わるプログラマー集団の腕が上がれば上がる程、Bug発生箇所の特定は難しい．
　腕が良ければ良い程、文法違反はますます減少し、計算手順が間違っている場合にさえ、 そうなのだ。対して初心者は、文法Errorになる箇所ではたいてい計算手順も間違っていて、 コンパイラーCheckで発見しやすい。そのような理由から、「Bug」修正として出来る事は、基本的に一つしかない。
　　「Bug」に気づいたら、該当コードを上から下まで、全部読解しCheckする．
　だからMain Routineが数十万行になるような書き方は、避けるべきなのだ。 そして最良の「Bug」対策は、それを出さない事だ。出さないために、どのような手を打てるのか？。 応えはある意味簡単で、プログラムが読みやすくてわかりやすい事。 それを実現する一番の方法は、プログラムが短い事である。これらだけでも、 Sub Routineを使う価値は十分にある。
　次に数千〜数万の個別プログラムを組み合わせたような、長大なMain Routineの中では、 同じ計算を繰り返し用いたり、ほとんど似たような計算をしたり、 同じ意味の変数を扱うものが多数現れたりする可能性が、高い。このような時には、 同じ意味の変数には同じ変数名を、是非当てるべきだ。
　意味と名前に固有の関係を結ばせると、注意力が分散しないので、 読みやすくてわかりやすいプログラムになる。プログラマーは大概、 自分の注意力の限界付近で仕事をしているので、注意の分散が少しでも下がると、Bugは劇的に減少する。 しかもたった一個のBug発生でも、基本は「全部読解Check」であるから、 この簡単なルールの適用の対費用効果は、途轍もなく大きい。ところがSub Routineを使わないと、 このルールの適用は出来ない。何故なら、
　　変数の意味は同じであっても、変数の内容は文脈依存．
であるからだ。そのために、変数名が際限なく増殖し、注意が際限なく拡散するという危険極まりない事態になる。 一方Sub Routineが使えれば、そこではLocal変数がサポートされるので、 同じ意味には常に同じ変数名を使用できるようになる。
　初期のBasicプログラムはそのようなものだった（N88 Basicの頃。もっとも数万行も書けなかったが）。 余りにもこんがらがっていたので、スパゲッティー・プログラムの異名を持っていた。 そのような危険を避けるために、構造化プログラミングが始まった。現在のObject指向は、 構造化プログラミングの子孫なので、Application構造は基本的に、必ず構造化されている。
　構造化プログラミングとは単純に言えば、Sub Routineを使ってMain Routineを整理しろ！、という事である。 ある程度複雑な計算は、Sub Routineを別途用意して、下請けに出す。
　形式論理のやり方にもそこそこ慣れてきたある日、形式論理がSub RoutineとLocal変数の原型をサポートする 事に気づいて、びっくりした。
　証明の方法、と言われるものがそれだ。典型的には「補助仮定の方法」である。 関係式Ａ⇒Ｂを証明したいとする。こうなる。
扱っている理論Ｔに、仮定Ａを付加する（これは任意にできる。Sub RoutineのCall）。
Ａを付加された理論をＴ'とする（Sub Routineに入る）。
Ｔ'において、Ａは自明に正しい（定理である）。
その事を全面的に利用して、Ｂを証明する（Ｂは、Ｔ'の定理）。
Ａを捨てる（Sub RoutineからReturnする）。
Ａ⇒Ｂは、理論Ｔの定理になっている（Sub RoutineからMain Routineへの復帰）。
（どうだろう？。私には、典型的なSub Routine Callに見える）
　Sub Routine 内のLocal変数とは、別々のSub Routineで同じ変数名が使われたとしても、 それらの内容は、決して重複しないという仕様である（メモリ領域が別々に取られる）。 この仕様によって、同じ意味の変数に同じ変数名を当てて、それらが別々のSub Routineで何回用いられようと、 変数の内容は別物になる。そのために変数名が際限なく増殖するという、危険極まりない事態も避けられる。

「補助定数の方法」
xを文字、ＡおよびＢを理論Ｔの関係式、Ｔ'をある理論とし、以下の条件を満たすとする。

1゜xはＴの定数でなく、Ｂはxを含まない．
2゜(Ｔ|x)ＡがＴの定理となる、Ｔの対象式Ｔがある．
3゜理論Ｔ'は、Ｔの公理にＡを追加して得られる．
4゜このとき、ＢがＴ'の定理なら、ＢはＴの定理．

　1゜の「xはＴの定数でなく」の部分は、とりあえず無視していい。 「Ｂはxを含まない」の部分が本質だ。1゜〜4゜を通して読めばわかると思うが、 これらは［4］のPrivate Sub Added (StartN，EndN，Total)と、Private Sub Added (S，E，T)の関係を 述べているのである。つまりSub Routineの結果（Ｂ）は、その内部Local変数の名前（xとＴ） とは無関係だと言っているのである。従って、Sub Routine内では、同じ対象式を何回も違った 意味や内容に使える事になる。
　「補助定数の方法」は「Ｔ∈Ｒ」といった宣言で始まる（Ｒは実数全体）。 このときＡ(x)は、x∈Ｒである。結論は(∀x)(x < x + 1) などだ。ここで(∀x)(x < x + 1)が、 xを含まない関係式Ｂである（xを含まない事は、限定作用素を持つ理論のところで述べる）。
　しかし形式論理が、Sub RoutineとLocal変数をサポートするのは、そんなに意外な事だろうか？。 最近は、そうでないと思っている。数学理論とは、きっと大規模Applicationなのだ。 そこでは既存のプログラミング言語として（意識しなくても）形式論理のLibraryを全面的に使用し、 人は自分の注意力の限界付近で仕事をする。しかもそこには、自動コンパイラーCheckすらない。 実用言語と同じようなApplication構造が、是非必要だったのだ。

［6］プログラム・パターン，Tips
　プログラミングの世界で、プログラム・パターンという用語が、ほぼ正式述語になったのは、 Object指向以後の事である。
　プログラム・パターンとは、ある同種のApplicationを書きたい場合に当然採用する、 定型的で典型的なプログラムの書き方の事を指すが、一般には、ProcedureやModuleの上位に位置する、 Applicationレベルでの上部構造の雛形である。ProcedureレベルやModuleレベルのものは、 たぶんTipsと言われる。これらの区別は確定したものではなく、どちらかというと業界標準に属する。
　遥か昔からパターン（やTips）は、「Tips集」という形で多くの書籍にまとめられてきたが、 それらはあくまで、Textベースだった。要するに書き写さなければならなかったのである。
　Object指向以来、プログラム・パターンは、いかなる言語にも適用可能なように抽象化され、 擬似コード化されて記述されるようになった。パターンは特定言語に固有のものではないからだ。 いまでは開発環境自体が、例えばコードスニペット機能でプログラム・パターンの自動適用をサポートしている。 プログラム・パターンは、コーディングを非常に効率化する。
　パターンは特定言語に固有のものではない。よってこの概念は、形式論理のプログラミングにも、当然適用できる。 形式論理におけるプログラミングとは何かという事は、すぐ後に説明する。 形式論理におけるプログラム・パターンとは、「推論法則」と呼ばれるものである。
典型的な例を揚げる。

　　Ａ ⇒ 〜〜Ａ （排中律）
　　(Ａ ⇒ Ｂ) ⇒ (〜Ｂ ⇒ 〜Ａ) （対偶）
　　Ａ⇒Ｂが定理で、Ｂ⇒Ｃが定理なら、Ａ⇒Ｃは定理（⇒の推移則）

（排中律）と（対偶）はほぼ確実にTipsに属し、（⇒の推移則）はどうちらかと言うとパターンと言える。 これらは一回でも証明されれば、当然の事として使われる。もっと具体的な数学でも、 そういうのはごまんとある。例えばxを実数としたとき、
　　　x ＜ x + 2
を使用するのを、ためらう人はいないだろう。もっと難しい例もある。
　　　コンパクト空間の閉集合は、コンパクト．
　これなどは実際に証明するとなると、けっこう鬱陶しいのだが、だからといって、 これを使う事をためらう人はいないし、これらを「明らか」として認める事により、証明が効率化される。 パターンの目的は、プログラミングにおいても数学においても、結局はそれである。 それによってプログラミングも数学も（形式論理学も）実用に耐えうるところまで、省力化できる。
　よって形式論理学において最も手をかけるのは、「推論法則」の証明であり、 使用可能なパターンリストのストックを増やす事が、理論の主目的になる。 形式論理におけるプログラミングとは、実際には、パターンたる「推論法則」を示していく作業だといえる。
　実用プログラミングにおけるSub Routine（Function）構造も本当はパターンである。 しかし余りにも汎用的で一般的な構造化パターンなので、構造化言語と呼ばれる言語 Package（C++，VC，Managed C，C#，VB，Java，Perl，Pascal，Lisp，Fortran，Cobol，Macro Assemblerなど皆そうだ） は、Sub Routine（Function）構造を組み込み機能として実現しているので、 それに関する手続きコードは書かなくて良い。一方、形式論理は、 これら形式言語に通ずる基礎を提供するものであるから、Sub Routine（Function）構造も「証明の方法」という 「推論法則」として示してから、使用する必要がある。この点は、実用プログラミングと違う。

［7］ノートの構成
　ここまで形式論理をプログラミング言語の側から読んで、対応を付けてきた （なので、そのぶん偏った見方だ）。さっきも言ったように形式論理学は非常に一般性を持った言語なので、 具体的な対応付けは、この辺りが限度である。それでも、これだけあれば、 「ブルバキ数学原論１ 第１章 形式的な数学の記述」の構成を述べられるところまで来ている。
　同書では、基本語彙と文法（構成手続き）、理論における代入（混成言語プログラミング）、 シェーマ（組み込み関数の仕様定義）、証明の全文（出力仕様の定義）が行われたあと、 「論理的な理論（命題理論）」，「限定作用素を持つ理論（第一階述語理論）」， 「等号を持つ理論」が順番に導入される。
それぞれの理論では、それぞれに固有のシェーマが導入され、後に続く理論は、 その前の理論のシェーマと結果を全て持っている。理論は、後の方ほど豊かになる
　以下では、OR，AND，Notを、ou，et，〜で表している。

第１章 形式的な数学の記述
§１．対象式と関係式
　１．記号，記号列
　　　論理記号，特殊記号も含めて、基本語彙の導入。⇒の仕様定義（ouと〜から定義される）。
　２．構成手続き
　　　文法と組み込み型（関係式と対象式）の仕様定義。

§２．公理
　１．公理
　　組み込み関数（シェーマ，明示公理，非明示公理）の仕様定義。
　２．証明
　　出力（証明の全文）の仕様定義。
　３．理論における代入
　　混成プログラミング方法の仕様定義。
　４．理論の比較
　　3.の続き。

§３．論理的な理論
　１．公理
　　固有シェーマの導入（ouと〜の仕様定義）。
　２．基本的な結論
　　基本Tipsの開発。
　３．証明の方法
　　基本パターンの開発。
　3.1 補助仮定の方法
　　Sub Rourine構造の開発。
　3.2 帰謬法
　　3.1の応用（背理法）。
　3.3 場合分けの方法
　　3.1の応用。
　3.4 補助定数の方法
　　2.3，2.4，3.3.1の応用（Local変数）。
　４．論理積
　　etの仕様定義（ouと〜から定義される）。基本Tipsの開発。
　５．同値
　　⇔の仕様定義（⇒とetから定義される）。基本Tipsの開発。

§４．限定作用素を持つ理論
　１．限定作用素の定義
　　τの仕様定義。∃，∀の基本仕様（τと〜から定義される）。基本Tipsの開発。
　２．限定作用素を持つ理論の公理
　　固有シェーマの導入（∃の追加仕様）。
　３．限定作用素の性質
　　基本Tipsの開発。

§５．等号を持つ理論
　１．公理
　　固有シェーマの導入（＝の仕様定義。⇒，⇔，∀，τから定義される）。基本Tipsの開発。
　２．等号の性質
　　等号に関する基本パターンの開発。
　３．関数関係
　　関数記号の仕様定義（⇒，∃，∀，τ，＝から定義される）。関数に関する基本パターンの開発。

　どうだろうか？。作業のほとんどは実用言語で言えば、言語リファレンス，開発環境，コンパイラー， リンカーに含まれる事ばかりだ。§1と2は、言語リファレンスであり、 以後はLibralyに属すのがふつうだろう。こんなのは通常の言語Packageでは、Packageを買った瞬間に付いてくるのに、 形式論理では、それらをTipsやパターンなどとしてプログラムする必要すらある。
というのは、開発環境やコンパイラーだって、本当は人が書いたプログラムなのだ（多くはC言語で書かれている）。 昔は、プログラミング支援プログラムと呼ばれていた。 形式論理学とは、本当に言語開発なのだと、あらためて思う。
　ノート外の事ではあるが、原著とした「ブルバキ 集合論１」では、この後「第２章 集合論」が、 「第１章」で開発した形式言語を全面的に使用する、数学理論第一号として登場する。

戻る