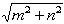NO.1713 正n角形の3頂点 2008.2.18 水の流れ
第204回数学的な応募問題
皆さん、2007年度大学入試問題集(数研出版)にある
慶応大学理工学部の入試問題を参考にして次の問題を作りました。
正n角形(nは3以上の整数)の3つの頂点でできる三角形について、次の問題に答えよ。
問題1:n=9のとき、
(1)三角形の個数を求めよ。
(2)鈍角三角形の個数を求めよ。
(3)直角三角形の個数を求めよ。
(4)鋭角三角形の個数を求めよ。
問題2:n=10のとき、
(1)三角形の個数を求めよ。
(2)鈍角三角形の個数を求めよ。
(3)直角三角形の個数を求めよ。
(4)鋭角三角形の個数を求めよ。
問題3:一般に、正n角形の3つの頂点でできる三角形について、
(1)三角形の個数を求めよ。
(2)鋭角三角形の個数を求めよ。(nが奇数、偶数に場合わけが必要)
(3)直角三角形の個数を求めよ。(nが奇数、偶数に場合わけが必要)
(4)鋭角三角形の個数を求めよ。(nが奇数、偶数に場合わけが必要)
問題4:nを無限大に大きくしたとき、正n角形は円に近づきます。円周上の異なる3点でできる三角形について、
(1)鈍角三角形となる確率を求めよ。
(2)直角三角形となる確率を求めよ。
(3)鋭角三角形となる確率を求めよ。
注:この記事に関する投稿の掲載は、2008年3月10日以降とします。
NO.1712 ガウスの格子点問題(3) 2008.2.18 夜ふかしのつらいおじさん
質問5
R(3)=R(7)=R(11)=0です。
R(N)は、原点が中心で半径が√Nの円周上の格子点の個数です。
x2+y2=NでNが奇素数であるとすると、
2数x2とy2は奇数と偶数になります。
x2を奇数、y2を偶数としてみます。
すると、xは奇数、yは偶数になります。
そこで、x=2m+1、y=2nとおきます。
x2+y2=(2m+1)2+(2n)2
=4×(m2+m+n2)+1
となるので4k+3の形の素数のときは、格子点にはなりません。
質問6
R(N)は、原点が中心で半径が√Nの円周上の格子点の個数です。
R(2N)は、原点が中心で半径が√(2N)の円周上の格子点の個数です。
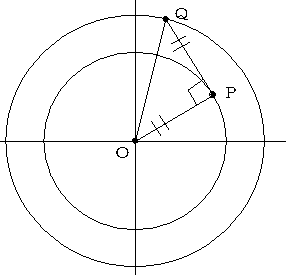
右図で点Pを半径√Nの円周上の点とします。
点Pが格子点なら座標を(m,n)と表せます。
点Pは、原点Oから右にm、上にnいった点です。
そのPから上にm、左にnいった点をQとすると、Qは格子点です。
また△OPQは直角二等辺三角形です。
すると、OQの長さは、√(2N)です。
つまりPが格子点なら、Qも格子点です。
点Pが格子点でなければ、Qも格子点ではありません。
格子点でないところから単位の長さの移動では格子点に乗ることができません。
このように対応を考えると、半径√Nの円上の点と
半径√(2N)の円上の点とが1:1になります。
だから、R(N)=R(2N)です。
質問7
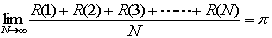 です。
です。
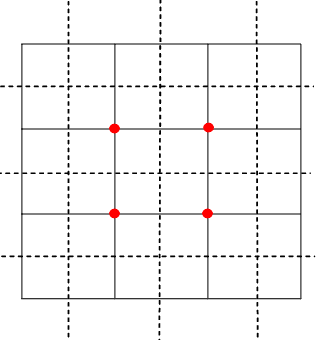
右の図で実線も点線も間隔が1であるとします。
点線で囲まれる単位面積の正方形の中に
格子点がちょうど1つずつ含まれています。
これは格子点の個数と面積とが等しいことを表しています。
格子点をもれなくだぶりなく数えればその面積を求めることができます。
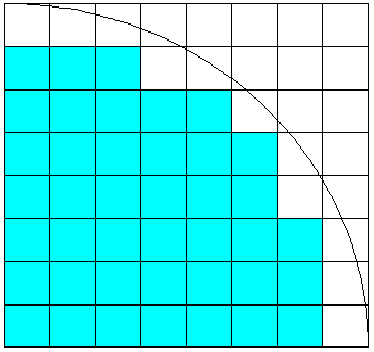
この問題でR(N)は原点からの距離が√Nである格子点の個数を与えています。
格子点(m,n)の原点からの距離は、
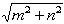
なので必ず自然数m2+n2の平方根の形になります。
問題の式の分子は、原点に近いところから格子点の個数を数えています。
つまり、半径√Nの円の面積をあたえます。
分母は、1辺√Nの正方形の面積です。
以上から極限値はπに収束します。
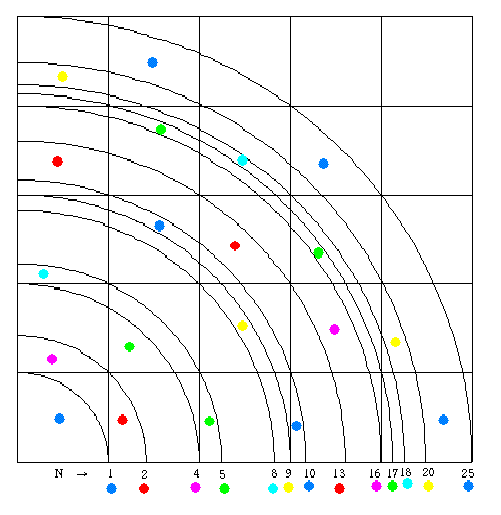
下の図は、R(N)/4の個数をだぶらないように単位の正方形の中に打点していったものです。
質問4
R(5)=8 格子点は、(±1,±2)、(±2,±1)
R(17)=8 格子点は、(±1,±4)、(±4,±1)
R(29)=8 格子点は、(±2,±5)、(±5,±2)
この証明は難しいです。
ガウス素数を簡単に説明できれば良いのですが手に余るので止めます。
NO.1711 ガウスの格子点問題(2) 2008.2.18 夜ふかしのつらいおじさん
質問1
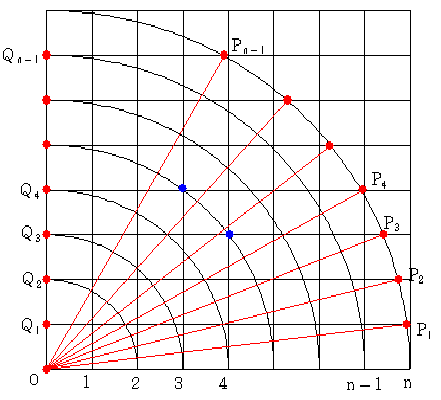
格子点の個数を横に数えることにします。
図は、半径2からnの同心円を表しています。
P(n)の個数を数えるのに、線分P1Q1、P2Q2、
・・・、Pn-1Qn-1の上を数えていきます。

質問2
次の計算より求まります。
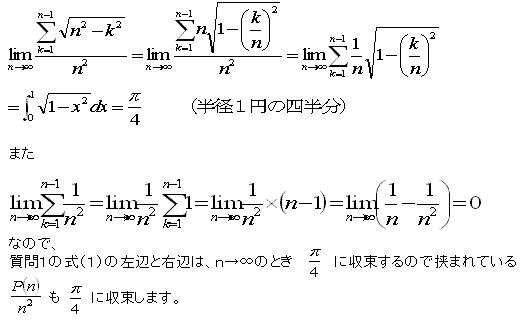
これは考えてみると当然のことといえます。
分子のP(n)は扇形の中の1辺1の正方形の個数にあたります。
分母のn2はその扇形に外接する正方形の面積にあたります。
だからその極限値は半径1の扇形の面積になります。
NO.1710 本:迷走する物理学 2008.2.11 DDT
リー・スモーリンを初めて知ったのは、この前つぶれてしまった草思社から出ていた
「量子宇宙への3つの道」です。この本が書かれたのは2000年、邦訳が出たのは2002年でした。
この中でスモーリンは次のように言っていました。
2015年までには量子力学の謎は解かれ、今世紀の末には、高校生が量子重力を習っている. (1)
この言葉を「Weekend Mathematics」で紹介したのは2005年の事で、非常に力強く感じたものです。
もっとも「私は大の楽天家である」と著者自身は語っていましたが。
リー・スモーリンの最終目標はTOE(Theory of Everyhing:万物理論)という事になるのですが、
TOEに関する多くの「トンデモ本」とは違ってその活動は、職業物理学者らしく、じつに地道なものです。
TOE理論(もちろん未完成)を目指した系譜には、現時点では概ね以下のものがあります。
- ニュートン力学
- マックスウエルの電磁気学
- 特殊および一般相対性理論
- 量子力学(場の量子論を含む)
- 特殊相対性理論と量子力学を結合させた、ディラックの電子論
- ゲージ原理に始まる統一場理論
- ワインバーグ・サラムの電弱統一理論
- クォークによる素粒子物理学の標準模型
- 標準模型に超対称性を適用した、標準模型と電弱統一理論と強い力の理論を含む、大統一理論
- ホーキングとペンローズの1970年代の研究
- ペンローズのツイスター宇宙
- ループ重力
- ストリング理論
- 超対称ストリング理論
- ホログラフィック仮説
スモーリンが大学院生となった頃(1970年代)、最初の11個までは既にあり、
修行時代には最初の2個を除いていずれの分野にも、何らかの論文を書いていると思えます。
そうでなければ、それぞれの分野に詳しすぎます。
ループ重力以後は、彼の専門領域と言っても間違いではありません。
一時はアインシュタインの再来とまで唱われました。これだけの人が(1)だと言ったので、
とても力強かったのですが。
それが、そのわずか1年後(原著2006年)に書かれた
「迷走する物理学,ランダムハウス講談社,2007年」で楽天家である彼が、
「我々は失敗したのだ」とこうまで落胆しているのは、ただ事ではありません。
何故2000年〜2006年の間に、彼がそう思うようになったのかは、本書を読めばわかります。
先に述べた経歴によって、逆に「失敗した事を悟った」のだと思います
(今世紀末に、高校生が量子重力を習う見込みは薄そうです)。
「量子宇宙への3つの道」を読んで思ったスモーリンの素晴らしさは、概念でものを語れるところです。
概念でものを語れれば、理論の構造,動機付けと目的を、技術的詳細はさておいて伝える事が出来ます。
本書もコペルニクス,ガリレイ,ケプラー,ニュートンから始まって、現代のTOEにいたる系譜が、
丁寧に解説されています。ストリング理論に達する頃には、ストリング理論がどのような物なのか、
概念的には見えるようになります。本書の中心テーマは、色々な意味でストリング理論です。
ストリングの発展史は、かいつまんで言うと次のようになります。1980年までの素粒子物理学の最大の成果は、
素粒子の標準模型の発見でした。それは、それまで数百も見つかっていた素粒子と、自然界の基本力のうち3つ
(強い核力,弱い核力,電磁力)を、1種類の粒子と1個の力で記述するもので、今まで実験と合わなかった事は1回しかありません。
その1回は陽子崩壊の観測で、これもまだ見つかっていないというだけの話で、確定はしていません
(しかるべき根拠に基づく確率計算から、もうそろそろ見つかっても良いのに見つかっていない、というのが現在までの結論です)。
問題なのは、その統一模型が15個ほどの自由定数を持っている事です。
その値は、実験から決めて代入してやるしかなく、現実に合うように調整すれば、完璧な理論となります。
しかし15個も任意定数を持っていては、やはり究極理論ではないだろうというのが本音です。何故その任意定数が、
その値を取らねばならないかを説明できないからです。
そのとき現れたのが、ストリング理論でした。その緒端には、角道夫という日本の物理学者
(ミチオ・カク。本当は日系3世)も関わっています。ストリングのアイデアを上手く定式化すれば、
15個の任意定数を決定できる見込みがありました。それも、たった1個の究極実在であるストリングを支配する、
たった1個の運動法則を仮定するだけで。
世界中の理論家が熱狂したのも無理はありません。スモーリンもその一人です。
ただしスモーリンは素直にも、ストリングのみを信じるという態度をとりませんでした(時代の趨勢はそうだったにも関わらず)。
この態度が、本書の執筆につながっています。
最初の結果は、量子力学と特殊相対性理論を考慮した上で無矛盾なストリング理論は26次元以内にある、
というものでした。空間3次元+時間1次元=4次元の他に、最大22次元の付加次元が、この宇宙には付随しているが、
それは見えてないという結果です。26次元の他にも、最低5次元とか10次元とかの多数のモデルも得られました。
これだけでも目が点になりそうですが、世界最先端の理論物理学者達は、こんな事ではひるみません。
最初に出て来た多くのストリングモデルには、タキオンが含まれていました。タキオンとは最低速度が光速で、
止まる事のできない虚の質量を持つ、超光速粒子です。つまりこれは無縁根です。
従ってタキオンを含まないように理論に制限をかければ、最大26次元は4次元に落ち着くかもしれず、
たくさんあるモデルも一つに絞れるかもしれません。これは「良い事」だと判断されました。実際それは出来ました。
超対称性をかければ(その意味は、本書で概念的にわかって頂くとして)、
次元は10次元まで落ちタキオンはいなくなり、可能なモデルは5つにまで減ったのです。
しかも望外の成果までついてきます。
素粒子の標準モデルに超対称性をかけると、粒子にも力にもなり得る1個の究極実在を持つ、大統一理論になります
(現実とは合わないようですが)。それと同じ事が、ストリング理論にも起こったのです。
素粒子の標準モデルを説明するために始まったストリング理論が、じつは物質も力をも統一する、
大統一理論に化ける可能性が開けました。再び人々は熱狂します。ただし代償がありました。
可能な5つのモデルは、150もの任意定数パラメータを持っていたのです。スモーリンがストリングに
疑問を持ち出したのは、たぶんこの頃からです。人々が熱狂する中、このような発想を持ちえたのは、
彼がじつに素直に、物理の正統路線を一歩ずつ登ってきたからだと思えます。じっさい彼は、
「最近のストリング理論家はストリングばかりやっていて、素粒子物理学を知らな過ぎる」と嘆きます。
現在では無矛盾という意味で可能なストリングモデルは、10150通りはあるとわかったそうです。
10150通りの物理的に可能な宇宙がある、という事です。その中には、我々の宇宙を表すものも確実に含まれるでしょう。
人々はそれを再び「良い事」だと判断します。我々は、自分の宇宙の法則を知りたいと思っていただけなのに、
「全宇宙法則」を手に入れたのかも知れない、という訳です。しかし「当初の目的はどこへいったのだ!」と、
スモーリンは喝破します。
「10150通りもの中から、我々の宇宙を探し出す検証実験は可能なのか?」「検証実験の計画すら立てられないようなものが、
まともな物理理論と言えるのか?」です。これでは標準モデルの方が、まだましです。
そこには15個の任意定数パラメータしかなく、しかも結論も確定していない実験と、1回合っていないだけです。
ではストリング理論は、まともな物理理論ではないのでしょうか?。その動機付けや手法、その後の発展を見る限り、
とてもまともな路線を歩んでいるようにも見えます。スモーリン自身も、ストリングが正当な理論物理学である事と、
結局はストリングが正しいかも知れない事は認めているのです。しかし彼は、職業物理学者の常識として、
「10150通りもの解があり、検証実験の計画すら立つ見込みがない」ならば、研究の方向を変えるべきではないのか?、と言います。
ストリングが正しいとしても、それが正しいとわかる見込みは今のところありません。
また反証する事も、現状では不可能です。実際上、10150通りもの可能性があっては確認できないのです。
そうであれば、他の方法や理論を用いて、少なくともストリングを確認しようとするのが常識ではないのか?、という訳です。
このような現状であるにも関わらず人々は、ストリング研究を止めようとせず、世界中の人材と資源とがそれだけに集中し、
実情として他の方向の研究が、ほぼ不可能になっている。それが問題だとスモーリンは言います。何故こんな事になったのか?。
これについては後述します。
スモーリンが概念で説明してくれたおかげで、ストリング理論が10150通りもの解を持つ理由を説明できます
(例によって、説明できると思っているだけですが^^)。
スモーリンは、アインシュタインの正統な後継者です。アインシュタインの一般相対性理論の真に革新的なアイデアは、
自然は「背景非依存」な点にあると彼は言います。ここで「背景」とは、物理理論を立てる場合に必ず用意する、
時間と空間の座標軸の事です。
例えばニュートン力学では、絶対に変化しない固定された絶対時間と絶対空間が仮定され、
その枠内を粒子が運動するという描像がとられます。
特殊相対性理論においても、絶対時間と絶対空間は相対的時空間(観測者によって変化して良い)に変わりますが、
観測者全体に対して、相対的時空間はやはり固定されたものです。相対性を実現するローレンツ変換は、
全ての観測者に対して一個しかなく、時空間は観測者に関して相対的に変化するものの、変換則が一個である以上、
時空間の実体は(それが何かは今もわかっていませんが)、やはり一個に固定されたものと考えられます。
これが「背景依存」の理論です。
運動を記述する(考える)ために、それが動きうる時空間(背景)を運動物体とは無関係に仮定し、
それによって決められた(依存した)形で運動を記述するからです。
この記述方法は日常と余りにも合っていたために、アインシュタインが、物理的現実の観察結果に基づいて得た
「等価原理」から一般相対性原理が導入されるまで、誰もそうでないとは気づきませんでした。
一般相対性理論において時空間は、その時点での物質分布によって変化します。逆に時空間の変化が、
物質の運動に、ひいては物質分布に影響します。それが重力の成り立ちです。
つまり一般相対性理論は、運動を記述する座標系の決め方まで、その理論の動作機構として含んでいます。
だから「背景非依存」と言われます。そして一般相対性理論は、現在の理論と技術、
両面の限界において実証された理論とみなされています。よって基礎理論はみな、「背景非依存」な形で定式化するべきだ、
という事になります。
ところが一般相対性理論以前どころか、それ以後の理論においてさえ、「背景非依存」で定式化され、
実証された基礎理論は無いのです。もう一つの実証された基礎理論、量子力学と素粒子の標準モデルは、
その検証精度たるや、一般相対性理論の1020倍も厳密に検証されたというのに「背景依存」の定式化です。
ストリング理論も、量子力学と特殊相対性理論までしか考慮していないので「背景依存」です。そして、実証されていません。
公平を期して言えば、「量子化され背景非依存で、かつ実証された基礎理論」もありません。
一般相対性理論は量子効果を含んでいません。それが量子重力理論の動機です。
しかしストリングが「背景依存」だから、それだけの理由で駄目だ、という事にはなりません。
定式化は、理論をどう表現するかの技術上の問題でもあります。数学的な仮想座標系として、
固定した時空間を、理論の記述方法の基礎に置く事は、自由にできます。その中に、現実の物理的観測から想定される、
既存の物理法則の適当な一般化を仮定し、粒子と力を動かしてみたら、動的に変化しうる重量場が現れたという事になれば、
それはそれで大成功なのです。何故なら、ストリング理論は重力(重力子)をほぼ必然的に含み、
一般相対性理論によれば、重力場と時空間は等価で、時空間こそが宇宙だからです。これに成功すれば、ストリング理論は、
「背景非依存」な宇宙の基礎理論のモデルを、得た事になります。
そういう意味では、超対称ストリングは大成功なのかも知れません。10150個にも上る宇宙の可能性を、
実際に導いて見せたからです。我々は、我々の宇宙の法則を知りたいと思っていただけなのに、「全宇宙理論」を、書いてしまった、
という言い分には一理あります。
しかし現実に知りたいのは、なぜ我々はその1/10150の宇宙にいるのか?という事です。
超対称ストリングは確かに正しいのかも知れないが、1/10150の選択を可能にする条件を見つけていない、
がスモーリンの主張です。その条件は現在、誰も知りません。
もちろんストリングの研究を続ける事によって、いずれはその答えがみつかる可能性もあります。
しかし、スモーリンは望みはないと感じています。それぞれの業界には、その専門知識を体で体得する事によってしか得られない
感触があります。理論物理学の正統的な階段を、一歩も踏み外すことなくやって来た彼の経歴をみるとき、
私はその感触を信じたくなります。
そしてもし、「背景非依存で物質も力をも同等に扱う大統一理論があった」としたら、
それはそんな事にはならない可能性が高いと、彼は言います。何故なら「背景非依存」な定式化は、
最初から時空間(宇宙)の決め方まで理論の解として含まなければならないので、「我々の宇宙が、なぜこうなるのか?」
に関する原理も、定式化の前提に当然含まれるだろうと。
そこで最も手っ取り早い方法として、「背景非依存な量子論をも考慮した基礎理論の定式化」を行っていけば、
その過程で、それが見つかるという考えは妥当ではないのか?、と彼は問うています。私には十分説得力がありました。
彼はその方面での第一人者です。しかも実際その方面で、その証拠はいくつか見つかっているし非常に大きな成果もあります。
実証されてはいませんが、「量子力学と、背景非依存な一般相対性理論とを結合」して形になった理論が、たった一つだけあります。
それはループ重力です。彼は、その創始メンバーの一人で主導者でした。
この事だけでもストリングの現状に対する彼の意見には、十分傾聴に値する価値があると思えます。
ループ重力は実証されていませんが、検証も反証もできないのとは違います。現在は無理ですが、
具体的事例を計算できるようになれば、検証可能な結果を出せるだろうと、その研究グループは踏んでいます。
10150通りもの解にはなり得ない。それが、その方面で見つかった証拠のいくつかです。
基礎理論としてのもっと有望な証拠もあるそうですが、それは本書の内容に譲ります。
以上の事が全てスモーリンの予想通りだったとしても、それでもなおスモーリンは、ストリング研究を止めるべきではないと言います。
彼らの研究が学会の主流(ストリング理論)からは、どちらかというと冷遇され続けてきた経緯を考えると、
これは感動的に公平な言葉です。彼は本当に、物理が好きなんだなと思います。
何故なら、10150通りもの宇宙を導けたストリング研究自体には価値があると、彼は本気で思っているからです。
背景非依存の研究にとっても、その成果は重要な道標になります。あらゆる宇宙を導いた成果は、ループ重力よりも
遥か先に進んでいるからです。
スモーリンは最初から、ストリングがループ重力の糧になる事に気づき、ストリングを本気で研究していました。
ループ重力もストリングへの助けになる事を望んでいました。でも実際には、後の方は拒否されたそうです。
もっと一般的に言うと、あらゆる研究方向があってしかるべきだと、彼は思っています。
スモーリンが本気でストリングに取り組んでいた証拠もあります。ストリング学会の年次総会の冒頭で紹介される、
総括論文の執筆を任されたのが証拠です。現行の成果をまとめ、将来への示唆を行う総括論文は通常、
その分野の指導的立場にある誰かが行います。スモーリン自身も、自分のところに総括論文の仕事が舞い込んで来た事が、
ストリング学会の異常さを示しているとは言っているのですが、任されたのがすごいと思えます。
ある意味門外漢なのに、実力はストリング学会の指導者レベルと判断されたとしか思えません。
彼は本気でストリングをやっていました。
では、ストリング理論の現状を誰もが知りながら、何故みんなストリングばかりをやりたがるのか?、に戻ります。
1980年代以降、物理学会は急速に組織化・官僚化されたのがその理由だと、彼は言います。この事自体は確かです。
物理学会に限らず、少なくとも1980年代以降の先進国では国家そのものが、それ以前のどの時代にも増して、
官僚化・組織化されています。小泉さんの規制緩和と構造改革も、官僚化の充実が進んだから、
ひとまず安定的に混乱もなく実施できたという、皮肉な見方もできます。官僚化の何が悪いのでしょう?。
官僚組織とは管理部門であり、非生産部門です。
今から200年も前に社会学者マックス・ウェーバーは、その当時で考えうる共産主義体制(社会主義体制)の組織構造を、
彼がほとんど独力で開発した組織論によって詳細に調べ、共産主義は必ず破綻する、と言いました。
その理由は、非生産部門たる官僚組織の肥大化です。生産しない管理機構のみが過剰に大きくなれば、
いずれは組織自体が破産します。その分析によれば、共産体制は官僚組織と異常に相性が良いのです。
ソ連の末路や北の現状を考えると、ウェーバーのとんでもない先見性が見て取れます。いまそれと本質的には同じ事が、
世界中の物理学会で進行している。多少の個人的見解で誇張はしてますが(以下も)。
官僚化されるとは「お役所仕事」の横行です。その最大の目的は、組織の永続化と利権の恒久化以外にありません。
「お役所仕事」の本質は「業務の継続性」という言葉に尽きます。
ストリング理論は何も、それ自身のために学会を官僚化したわけではありません。
ストリング理論が最初に大流行した1980年代(第一次ストリング革命)のちょうどその時期に、
たまたま物理学会の官僚化が始まっただけです。その頃最も見込みのありそうで、
これから発展するであろう基礎理論は、ストリング理論でした。実際そうなりました。
そのために物理学会は、そのような人材を可能な限り集めるために、
それ向けの研究助成制度や審査基準,就職面接体制を作りました。
しかし特定分野の人材や研究を優遇すれば、そこに利権が発生し、
利権は組織の永続化をもたらす最も有効な手段です。逆に利権を常時確保するために、組織は変化を嫌います。
ストリングだけが優遇され続けます。
「当初それは正しかった。しかし現在は2006年である。その結果我々は1980年から25年間も、
本質的な進歩を何も遂げていない」
科学の歴史は古代も含めれば、数千年になります。25年くらい何だっていうんでしょう?。
そんな時期もあるかもしれません。そこでスモーリンは、どんなペースで科学が進歩してきたか、語ってくれます。
彼によれば、少なくともコペルニクス以来、数十年に一回は革新的な進歩があったとなります。
特に1980年までの200年間は、それが25年に一回のペースだった。
1780年といえば、ニュートン力学がイギリスから海を越えてヨーロッパ大陸に定着し、
それを武器としたオイラーやベルヌーイなんかが、それまでのあらゆる難問を、当たるも幸いとなで斬りを始めた頃です。
そんな元気な時代が200年も続いたのに、突然1980年以降何も出なくなり、その状態で26年(いまや28年)、
しかもまだまだ続きそうだとなります。このスモーリンの感触も、やはり彼の経歴から考えて私は信じられます。
セッションを開いても常連が10人くらいしかいないような、分科会レベルのものであっても、いいですか、
そんな中にさえ派閥はあるんですよ。しかも排他的な事この上なくて、閉口します。
それが世界規模の一大勢力に意図していないとはいえ、国家の保護が付いたような形になったら、
ストリング以外の研究をまともに出来なくなるのは、あながちあり得ない事態ではないと思います。
25年の間、本当か嘘かもわからず、確認する術さえない理論に、世界中の資源と人材を投入し続け他の事をやらなかった。
生産力は落ち、非生産的な組織を拡大する既得権益だけが守られた(意識してアジってます)。
本書の最終章では物理学会の現状が分析されます。続いてクーンのパラダイム論を使って、理論物理の現状も分析されます。
二つの結果をもとに、現状を打開する、かなり現実的と思える提案がなされます。
しかし、このほんのささいな改革案の実現さえ危ぶまれるのが、既得権益の恐ろしさです。
スモーリンは本職の社会学者ではもちろんないので(アジったから言いますが、私もそうです。もと民青でもないですよ^^)、
最終章はここだけ食い足りないと思う向きもあるかも知れませんが、印象深い話がいくつも載っています。
特に、スモーリンはファイヤアーベントの自宅に行った事があり、生前の生身のヴィトゲンシュタインにも会ったというくだりは、
ちょっと羨ましかったです。ファイヤアーベントの「方法への挑戦」を初めて立ち読みした時は、
うさん臭い印象があって買う気が起きなかったのですが、スモーリンの描くファイヤアーベントの人柄は、
想像していたものと全然違ってました。もっとも経歴は無茶苦茶でしたが、
自分も経歴が無茶苦茶である事にかけては人後に落ちません(← って、自慢していいのか?)。
それにしてもスモーリンさん、哲学好きですね。でもそれが、彼の学問の根幹に横たわっています。
本書は失敗した世代の代表として、では次世代には何を残せるのかと、自責の念を込めて書いた啓蒙書だと思えます。
「ストリング理論を越えて」の章は、「広く知られてはいないが、こんなにわくわくする観測や実験や予想がいまや進行中だし、
ストリング以外にも、こんなにも面白い話がある」という話題に満ちています。
リー・スモーリンは今年で54才、現役でいられるのはもう10年くらいでしょうか?。本書は、引退迫った著者が、
この瞬間にも理論物理学に憧れ続けている、世界中の全ての中高生達に贈った「贈る言葉」なのです。
総評として言えば、いつものようにスモーリンの語り口は直線的に素直で、
魅力的な本に仕上がっている。読む苦労はないとは言わないが、辛口のブルーバックスと言えなくもない。
考えた程度に応じて、それなりに理解できる。概念で語る事の名手である彼は、考える材料は豊富に用意してくれる。
これは、失敗した世代が次の世代に贈った「贈る言葉」だ。そしてスモーリンはアインシュタインと同じように、
愚直で素直な実在論者だと思う。
[参考文献]
(1) 量子宇宙への3つの道,リー・スモーリン,草思社,2002年.
草思社はつぶれてしまったので、絶版になりそうです。
(2) 物理学の論理と方法 上(古典力学から素粒子論まで),菅野礼司,大月書店,1983年.
絶版です。上下とも復刻請願中。
(3) 場の古典論,ランダウ・リフシッツ,東京図書,1978年.
第1章全部と、各章の概説部分。現在17版が出ています。相変わらず大人気ですね。
(4) 官僚制,三戸公,未来社,1973年.
1984年の復刻版があるそうです。
(5) 故郷喪失者たち(近代化と日常意識),バーガー・ベルガー・ケルナー,新曜社,1977年.
絶版です。バーガー(ウェーバーの継承者)の著作は売れ行きが悪く、復刻も遠いとの事。
(6) 科学革命の構造,トーマス・クーン,みすず書房,1971年.
驚いた事にみすず書房で調べたところ、ご存命でした(本が)。密かな根強い人気なんですね。初めて読んだ時には、
科学は合理的に進歩はしないという見解に不信感をおぼえたものですが、その後色々なものを見たせいか(歳のせいで)、
概ね当たっているんじゃないかと思うようになりました。クーンの10年後(くらいかな?)に、
クーンへの再批判として、そのものずばり「科学は合理的に進歩する,L・ローダン,サイエンス社」なんてのもあったのですが、
サイエンス社に行って調べてみたところ、きれいさっぱり消えてなくなってました(Amazonにはまだあるみたいです)。
「白亜紀に夜が来る」という読み物としても面白い、恐竜隕石絶滅説はいかにして定説となったかが書いてある本があるのですが、
隕石説が地学学会でも認められるようになったのは、明確な証拠が出てきたからでも(かなり明確な証拠は当初からあった)、
反対者達が納得したからでもなく(最後まで無視し続けた)、たんに現役が世代交代したからだというのが、そこでの結論でした。


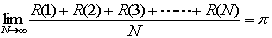 です。
です。